重视课本习题的补充价值

刘祥云

（江苏省兴化市楚水实验学校，225700）

蔡上鹤教授认为，教科书是由正文、例题和习题三部分有机组成的.课本习题是许多专家、学者、权威人士根据长期以来的积累沉淀，经过深思熟虑、精挑细选、反复斟酌编排而成的.课本后的习题，不仅具有巩固新知、拓展延伸之功效，还具有对课本内容进行补充说明的价值.深挖课本习题的补充意图，对构建完整的知识体系，提升分析问题、解决问题的数学“高阶思维”，是至关重要的.

一、一题多解，补充课本综合性

三角、向量、解析几何的知识点经常有交汇，综合性较强.但课本是按知识点编排的，缺乏综合性，这三个部分不可能安排单独一个章节，所以通过习题来体现这种思想.比如，“证明：平行四边形四边的平方和等于两条对角线的平方和.”同时出现在“直线的方程”、“余弦定理”、“向量”三个章节中，就暗示我们解决一个平面几何问题，可以分别从这三个角度去思考，实现一题多解.学会对习题的归纳，加深知识点的联系，形成知识网络，是提升数学学习能力的一种重要的手段.

例1 （2018年江苏泰州一模）如图1，已知矩形ABCD的边长AB=2，AD=1，点P，Q分别在边BC，CD上，且 ∠PAQ=45°，则的最小值为_______ .

1.解析法

以点A为原点，线段AB，AD所在的直线分别为x，y轴，建立直角坐标系.

设点Q（x，1），P（2，y），其中x∈ （0，2），y∈ （0，1），则

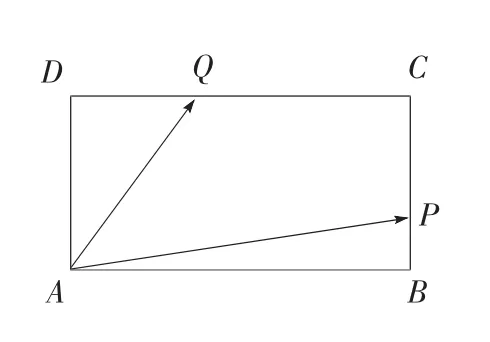
图1

因为xy∈ （0，2），所以2x+y=2-xy，所以有

2.向量法

3.三角法

二、多题一解，补充课本的统一性

在“圆锥曲线与方程”这部分的第五节“圆锥曲线的统一定义”中，给出三种曲线的统一形式，从更高的形式上揭示圆锥曲线之间内在的关系，充分感受了数学内在的、和谐的美.

在“数列”中，章节设计为

例2 已知数列｛an｝中，an=n2，求数列｛an｝的前n项和Sn.

三、举一反三，补充课本的一般性

“向量”这一章对于向量在三角形的重心、外心、内心、垂心的应用并没有涉及.但是向量的加法与减法运算离不开三角形，所以课本中仅有一道关于重心的习题：“已知三角形的三条中线交于一点G（也称为三角形的重心），且G点将每条中线分为2∶1，求证：.”该习题中有这样的信息：若G为重心，则，且有S△BOC=S△COA=S△AOB；反之，若G是 △ABC内部一点，如果满足和S△BOC=S△COA=S△AOB其中之一，那么G点为重心.本章节尽管没有将外心、内心、垂心在习题中体现，但是我们可以通过这道题进行延伸，将问题一般化，可得如下一例.

例3 如图2，若O是△ABC内部一点，有S△BOC∶S△COA∶S△AOB=λ1∶λ2∶λ3，则

图2

由此在锐角△ABC中可以得到内心、外心、垂心的性质：

其中 ∠BOC=2∠BAC，∠BOA=2∠BCA，∠AOC=2∠ABC.

则有S△BOC∶S△AOC∶S△AOB=sin 2A∶sin 2B∶sin 2C，所以sin 2A·

图3

性质3 若O是△ABC的垂心，则有S△BOC∶S△AOC∶S△AOB=tanA∶tanB∶tanC，

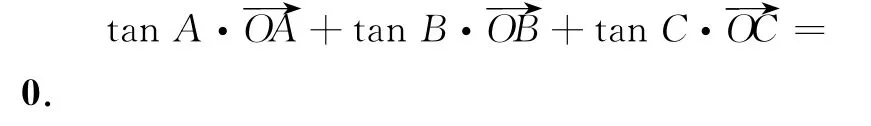
证明 如图4，在锐角 △ABC中，延长AO与BC相交于点D，则AD⊥BC.

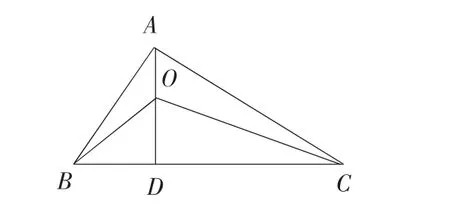
图4

教材中的每道习题都有其作用，在教学中，充分挖掘教材所蕴含的数学知识与方法、解题思路与策略，才能更好地理解教材的编写意图，更好地理解教材中“难言之隐”，从而不断提升自己的认知水平及发现问题、解决问题的能力.