感受数学对称美的三个重要途径

唐金波 林 丹

（广东省深圳科学高中，518129） （广东省深圳市龙岗区平湖实验学校，518100）

罗素曾经说过：数学，如果正确看它，不仅拥有真理，而且也有至高的美.克莱因也曾说过：数学是人类最高超的智力成就，也是人类心灵最独特的创作，音乐能激发情怀，绘画使人赏心悦目，诗歌能动人心弦，哲学使人获得智慧，科技可以改善生活，但是数学却能提供上述这一切.从数学大师的语言中可以看出，数学美是一种至高无上的美，美得令人陶醉，美得让人心驰神往，美得让人一发不可收拾.而且数学美有很多方面，本文仅就感受对称美在数学教学中的途径进行探讨.

什么是数学对称美？“对称”一词来自希腊语，其含义是“和谐”、“美观”.著名数学家、物理学家外尔说过：“对称是一个广阔的主题，在艺术和自然两方面都意义重大.数学是它的根本，并且很难找到可以论证数学智慧作用的更好的主题.”著名物理学家杨振宁也说过：“对称，非常重要，非常基本，哲学家、科学家很自然会广泛应用.”

从数学发展的历史来看，对称美一直伴随着数学的发展而发展.对对称美的追求，在一定的程度上也促进了数学的发展，成为创造好的数学和完善性重要思考的组成部分.在数学中伴随对称美而生成的数学概念和理论不计其数，比如，正数与负数、加法与减法、加法乘法的交换律、函数的奇偶性、函数与其反函数、对数与指数、微分与积分、度量空间与其对偶空间等，这些都视为对称美在数学中的体现.

总之，对称美在数学中是普遍存在的，数学家们大都对数学对称美有很深的感触，他们在创造数学的过程中欣赏着、品味着各式各样的对称之美，将它作为一种思想和原则来加以应用，并且能深入诠释数学对称美的美学价值和意义.

让学生在学习数学知识的同时认识到数学对称美的价值，不仅能使学生学会和理解从审美学的角度来学习数学、欣赏数学，而且在一种十分美妙的精神世界里把对数学的学习和探究活动变得充满乐趣和富有魅力.然而，教师在教学中都忽略了如何引导学生去欣赏对称美.那么如何让学生在学习中感受到数学对称美和对美的体验呢？感受数学对称美的途径有哪些？笔者结合自己的感悟和教学实践谈几点想法，敬请同行指正.

一、在数学定义和定理中感受数学对称美

教学中常常发现，有些学生对概念、定理的理解往往是停留在肤浅的层面，对概念一知半解，并没有理解其中深刻的含义，对其中所蕴含的对称思想感受不到.因此，在教学中，巧妙地利用概念和定理的对称性，能很好地帮助学生加深对概念的理解，让学生在感受数学对称美中领悟数学的魅力.

在学习函数奇偶性时，奇偶函数的定义是这样的：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）=f（x）（-f（x）），那么函数f（x）就叫做偶（奇）函数.在教学中大部分教师都没有注意到奇偶函数定义中所蕴含的对称思想和对称美，而仅仅从一般概念教学的角度去进行教学.仔细品味，这两个定义中包含有如下对称思想：一个x与一个-x对应；自变量x的函数值与自变量-x的函数值对应；一奇与一偶的对应，而一奇一偶又是一负一正的对应；由函数符号的对应，又不难想到函数图象的对称.定义中的这些对应，无一不向我们展示着数学的魅力和令人陶醉的对称美.通过这些对称美的欣赏，不仅能让我们较快地掌握数学知识，加深对定义的理解，更能帮助我们提高审美的体验和理解数学的本质.

数学对称美也表现在数学定理中.如正弦定理：

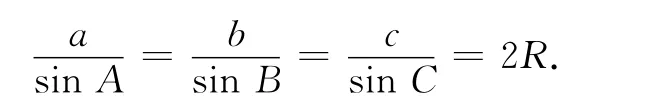
简洁明了地概括了三角形三条边、三个内角以及外接圆半径之间的关系，结构巧妙，具有非常美妙的对称性.又如，余弦定理：

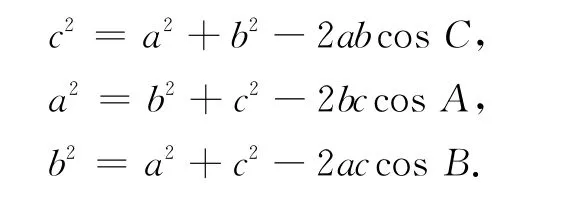
因为三角形的边、角都是对称的，由c2=a2+b2-2abcosC这个结果，把边a，b，c和对应的角A，B，C相应的换一下，就非常容易地得出了第二、三个结果.多么美妙简洁！揭示数学定理中的这种对称美可以让学生学会思考，领略数学的本质、和谐与美妙.

二、在数学公式、图形中感受数学对称美

数学公式的对称美给人一种和谐的感觉，一种极易推广和包容的审美.例如，加法交换律a+b=b+a，其中a，b互换后仍然成立，体现的是一种简洁的对称美.而这种对称也不失一般性，可以把它推广到群论就是交换群.如果再加入乘法a·b=b·a，可以构成环、域和线性空间等.如此简洁的公式却体现出了数学的一般规律和极大的包容性.还有，在学习二项式定理时，我们把n=1，2，3，…的二项式系数表示如下：

图形的对称具有很好的直观性，感官上更容易给人带来美的体验.而几何图形中的对称图形给我们呈现的是一种极为普遍的对称美.如轴对称图形、面对称图形和中心对称图形.圆既是中心对称图形也是轴对称图形，球是最完美最简洁的对称几何体.毕达哥拉斯学派认为：“圆是一切平面图形中最美的，球是一切立体图形中最美的”.因此，在教学中，教师应该及时引导学生去发现数学美，让学生学会用数学美的眼光去欣赏世界，表达世界.

三、在超越数学知识后感受数学对称美

数学的概念、公式和定理是人类大脑抽象思维的产物.人们在创造数学概念、公式与定理时，一方面要依据事物本身的规律，另一方面是高于事物本身的思维上的美学欣赏.而这些美学的感受，有时往往超越了数学知识的本身.例如，我们学习过集合之后，就会身临其境地感受到，数学家们在创造其规律和形式的时候，必定依据了某种美学思想.当进一步了解了群、线性空间、拓扑空间之后，更加能感受到数学之美.所以当我们的数学知识积累到一定的程度，就会抛开具体知识而感觉到一种美的体验，是一种数学的抽象之美、简洁之美和对称之美.

从心理学的角度看，数学教学要发展学生的核心素养，加强审美体验，就应遵循心理发展规律，加强学生对数学对称美的感受或体验.对于教师来说，要从数学教学的“功利性倾向”转向“审美性倾向”，需要更多地了解数学对称美的本质问题，以及如何深层次地感受数学对称美.对学生来说，它不仅能够锻炼学生的思维，拓展学生的视野，丰富学生的想象，给学生以美的感受，更是一种重要的数学思想、数学思维.数学教学不仅要引导学生探究知识本身的细节，还要引导学生领悟数学知识、数学问题的对称性和对称美.