基于“学生主体”的一轮复习教学设计——以“基本不等式及其应用”为例

秦晓龙

（江苏省苏州第十中学，215006）

《普通高中数学课程标准（2017版）》在“高中数学教学观”部分指出，“高中数学教学以发展学生数学学科核心素养为导向，提倡学生独立思考、自主学习、合作交流等多种学习方式，激发学习数学的兴趣，引导学生把握数学内容的本质.”基于对“新课标、新理念”的思考和探索，笔者就如何充分尊重和发挥学生的主体性开设了一堂高三示范课.

一、教学简介

1.开门见山，直奔主题

上课伊始，笔者先展示了最近几年考查“利用基本不等式求最值”的江苏高考真题与省内各地的模拟试题.

设计意图 通过展示考题，突出基本不等式的重要程度，激发学生主动学习的动力和兴趣.

2.课前热身，自主学习

（1）已知a，b∈R+，ab=1，则a+b的最小值为_______.

（2）已知a，b∈R+，a+b=1，则ab的最大值为_______ .

（3）判断下列结论是否正确，并说明理由.

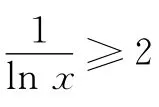
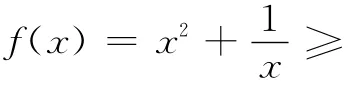
师：大家已经提前预习了本课的学案，下面请同学们来说说你的想法和结果.

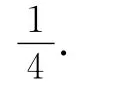
生：①中lnx可取负数，结论错误；② 中x2与的乘积不是定值，不能直接用基本不等式求最值，结论错误；③ 中取等条件不成立，结论错误.

设计意图 通过课本改编题，引领学生课前自主学习，复习并熟悉运用基本不等式求最值的方法，尤其是解题过程中要注意“一正、二定、三相等”.

3.经典例题，合作探究

师：这题是以一元函数为背景的利用基本不等式求最值问题，通过“配凑”可求出（1）的最小值为3（用投影展示了学生规范的解答过程），（2）如何求解呢？

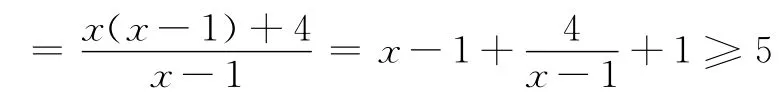
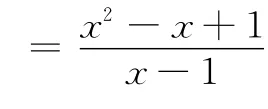
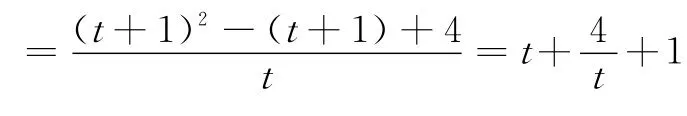
师：很好，通过“换元”等价化简目标函数，本质上还是利用“配凑”求最值这种解法是处理此类“高低次分式”的通法，那（3）又如何求解呢？

生：这个函数表达式通分后也是高低次分式，可以仿照（2）的做法，先换元化简，再配凑求最值.

师：还有其它解法吗？

生：注意到x+（1-x）=1，可以运用“常量代换”.

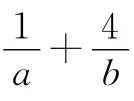
设计意图 通过多角度展示“高低次分式”，让学生感受其中不变的本质，从而理解和掌握解题的通法 —— 配凑，并能尝试灵活运用“巧解”.

例2 （1）若a＞0，b＞0，（a-1）（b-1）=1，求a+b的最小值；

（2）若a＞0，b＞0，2a+b+6=ab，求a+b的最小值.

师：对于（1），希望大家能发散思维，尽量从不同角度来解决.

生：用“配凑”，即a+b= （a-1）+（b-1）+2≥4，当且仅当a=b=2时取到等号.

师：a-1，b-1是正数吗？（学生答不上来，其他同学也沉思中.）

师：注意到条件中a＞0，b＞0如何运用吗？

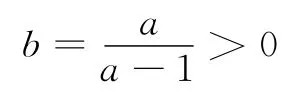
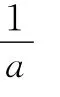
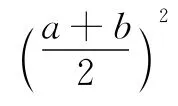
师：非常好，大家通过相互合作交流，归纳出了常用的几种解法，那么趁热打铁，我们能运用这些解法来处理（2）吗？

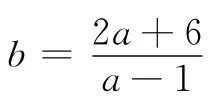
很多学生都露出了赞同的表情，但笔者没有马上给出结论，而是用期许的目光扫视着所有学生.课堂一下子安静了，但思维在高速地运转着.

瞬时，班级里爆发出了掌声和欢呼声.

设计意图 求二元关系的最值问题是考试的热点.通过经典陈题，多角度调动学生思维，引导学生发现、归纳方法并能触类旁通.

二、反思

高三数学一轮复习是一个系统工程，从各个教学环节中可以一览端倪.目前普通存在以下问题.

1.教学定位不准确

把复习课当作习题课，过分注重训练，忽视对数学概念的准确理解和记忆，忽视对数学思维的培养；混淆一轮复习与二轮复习的教学要求，过份深挖难度，花费大量精力钻研难题，忽视利用知识的横向联系建立完整的知识链体系.本节课通过课本改编题，引导学生自主复习和准确理解公式及其使用条件；通过经典例题，借助学生的解答将知识的运用从“一元问题”拓展到“多元问题”.例题的设计以学生的“最近发展区”为基准，难度适中，保障了课堂上学生的获得感.

2.教学目标不明确

高三教学任务非常繁重，为图省事，按照教辅书的编排照本宣科，忽视每堂课的具体教学目标；教学内容是相关习题的堆砌，随意性、盲目性强，忽视教学内容的系统性、针对性，没有明确这堂课到底要解决什么问题.本节课的教学目标是利用基本不等式求最值，上课伊始就通过情境引入、课前热身让学生明确；通过相互联系的例题，环环相扣的设问，系统地探究和归纳了解决问题的思想和方法.

3.“师生地位”不合理

老师“一言堂”，学生陪着“玩”，忽视老师的引领作用，学生才是学习的主体；注重课堂大量的习题，学生做得多，悟得少，忽视留出足够的时间引导学生独立思考、自主学习、合作交流，这样必然导致学生自主学习性差，教学效率低.本节课在施教前，笔者已熟悉和了解了学生的认知水平，通过合理设问，调动学生的积极性，主动参与到探究过程中.在整个教学过程中，教师始终担当的是“引领者”，充分尊重和保障了学生的“主体性”，从而使学生收获学习的成就感.

正如数学家陈省身所言：“数学是自己思考的产物，首先要能够思考起来，用自己的见解和别人的见解交换，才会有很好效果.”基于“学生主体”的数学课堂应该是启发学生思考的课堂，这需要教育工作者孜孜不倦地探索与实践.