创设情境 考查素养 明确方向— —以2019年高考数学全国卷解析几何题为例

许 磊

（江苏省南京师范大学附属中学江宁分校，211100）

“巧设情境呈现和创新设问方式”已成为基于核心素养的高考命题的基本原则.从2019年高考数学全国卷解析几何题的命制可以看出，命题者以平面几何知识与圆锥曲线的定义相结合作为突破口，着力考查考生直观想象、逻辑推理、数学运算核心素养.本文对此作出深入分析，供大家参考.

一、求离心率

求离心率常见于高考数学中的选择、填空题，考查综合运用平面几何、向量等结合圆锥曲线知识解决问题的能力.

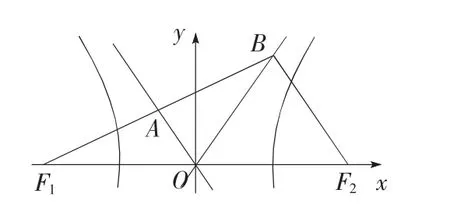
图1

反思 将上述解法对比，可以发现：法1运用平面几何去处理解析几何问题，可以极大地减少运算量，快速解决问题.

分析 联立以OF为直径的圆及圆x2+y2=a2，找到基本量的关系，计算得

反思 两圆相交可以利用两圆相减求出相交弦方程，从而找到a，b，c关系.本题主要考查双曲线和圆的性质，双曲线离心率的计算，转化与化归思想及数学运算素养.

二、求曲线（直线）的方程

求曲线方程（轨迹）是高考常考题，情境呈现方式具有较强的策略性.常将直线、圆、圆锥曲线相结合考查，体现综合分析、处理问题的能力.

例3 （2019高考数学全国卷1理科第10题）已知椭圆C的焦点为F1（-1，0），F2（1，0），过F2的直线与C交于A，B两点.若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为（ ）

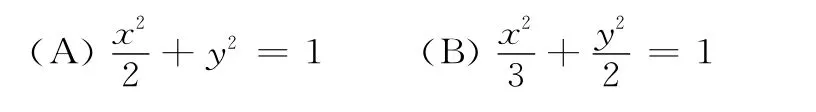
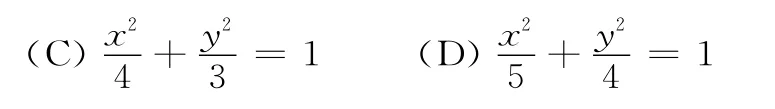
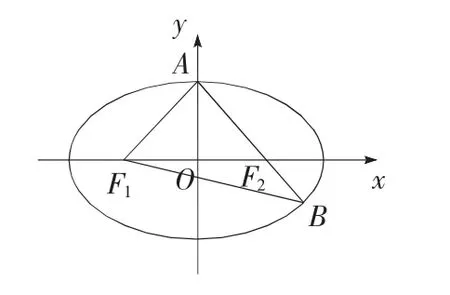
图2

反思 本题考查椭圆标准方程及其简单性质两者的综合运用，属于中档题，难度适当.考查数形结合思想、转化与化归能力，很好地落实了直观想象、逻辑推理、数学运算的数学素养.

三、求三角形的面积及最值

通过去探究三角形、四边形等几何图形面积的算法，综合考查数学运算素养，函数与方程思想，数形结合、转化与化归思想等.

（1）求C的方程，并说明C是什么曲线.

（2）过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连结QE并延长交C于点G.（i）证明：△PQG是直角三角形；（ii）求△PQG面积的最大值.