分类例说构造法在数学解题中的应用

沈 重

（江苏省吴县中学，215010）

所谓构造法，是指当某些数学问题按照定式思维思考不出结果时，转变到从另一个角度去寻找问题的数量、结构、条件与结论间的关系特征等，从而构造出新的数学对象或问题形式，使原来隐晦不清的特性在新构造出的数学对象或问题形式中清晰地展现出来，达到简捷地解决数学问题的目的.

古人云：工欲善其事，必先利其器.在解答数学问题的过程中，解题方法正是解题之“器”.而“数学构造法”便是解题方法之一.本文围绕中高考命题趋势，借助多个典型题目来分类探讨数学构造法在解题中的应用.

一、构造方程

顾名思义，即通过构造方程式来帮助我们解题，最常见的是构造一元二次方程（组）来解决问题.

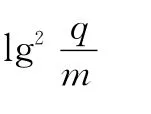
证明 构造方程

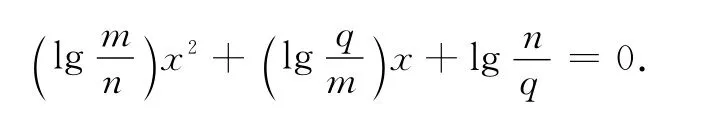
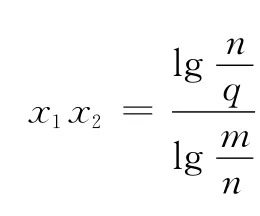
例2 （2011年浙江高考题）设x，y为实数，若4x2+y2+xy=1，则2x+y的最大值为_______ .

分析 直接分别求x和y的值几乎不可能，因为方程只有一道而未知数有两个，所以可考虑将2x+y看成一个整体，通过构造法直接求出其范围.

解 设t=2x+y，则原式可化为t2-3xy=1整理得

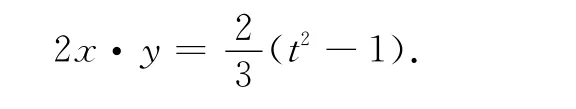
由韦达定理，可构造新一元二次方程

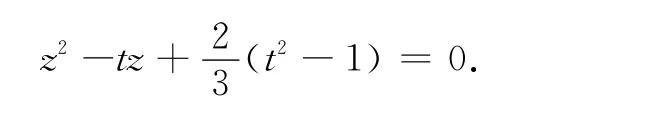
（该方程两根分别为2x和y）

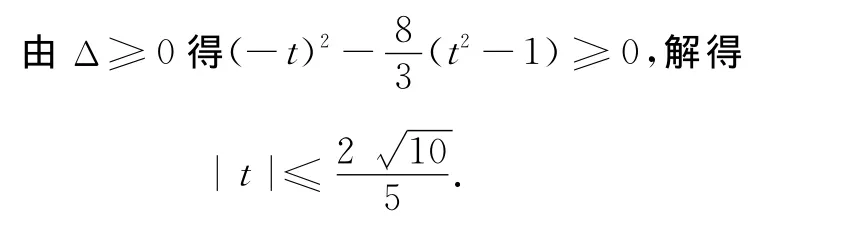
评注 构造方程是数学解题中使用频率较高的一种方法，且其中又以构造一元二次方程为主，因为一元二次方程及其相关知识点是初高中学习的一个重难点.从典型例题中发现，与一元二次方程构造有关的往往始于根与系数的判别式Δ=b2-4ac，所以解题时须密切关注与之相似或有关的条件，借以构造适当的方程辅助快速解题.

二、构造图形

图形构造法，是指当问题条件的数量关系有明显的几何意义或能以某种方式将问题转化为几何图形来体现，借助几何图形的性质研究，从而获得问题的解法的方法.

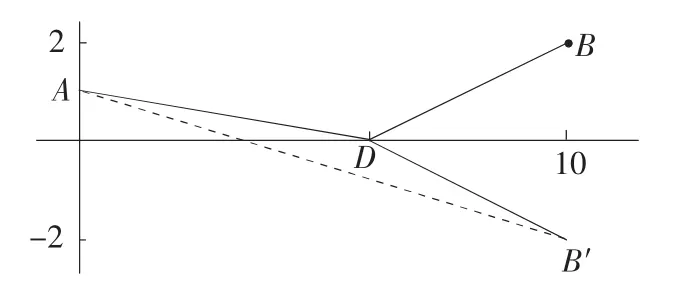
图1

如图1，在平面直角坐标系中作点A（0，1），B（10，2），D（a，0），B′（10，-2），则

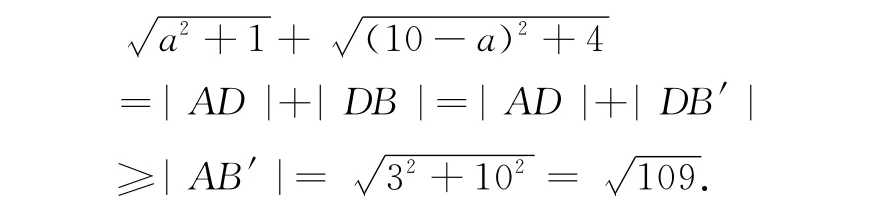
例 4 已知a，b，c为正数，证明

证明 如图2所示，在平面上取一点O，作 ∠AOB= ∠BOC= ∠COA=120°，OA=a，OB=b，OC=c.由余弦定理可得

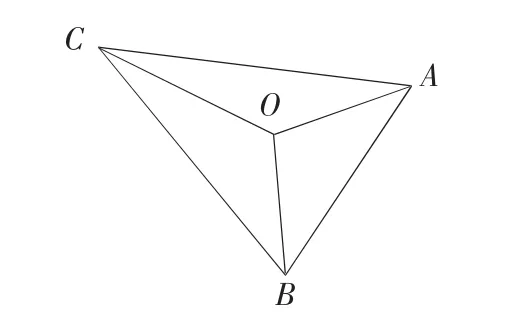
图2

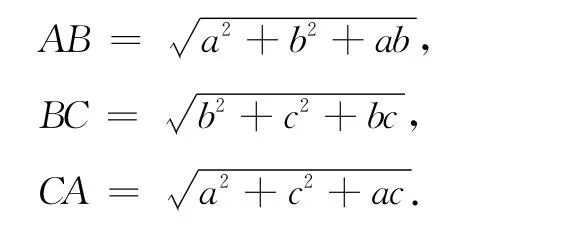
而三角形中两边和大于第三边，故AB+BC＞AC，即

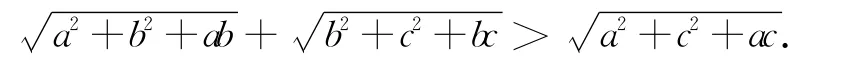
评注 在中学数学解题中，常见的证明不等式、求最值等问题，只要能挖掘出其几何意义，那么都有可能应用到构造图形的方法来解决.例如所给条件中伴有根式时，我们可以联想到构造点与点、线与线之间的距离关系来解决问题.

三、构造函数

构造函数法，指结合题设条件，构造适当的函数，通过函数的性质辅助解答问题的方法.

例5 已知x＞0，求证：

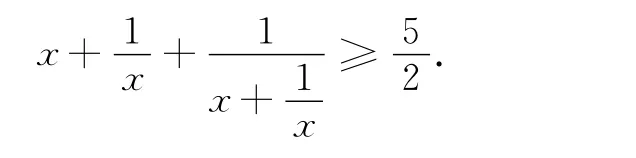
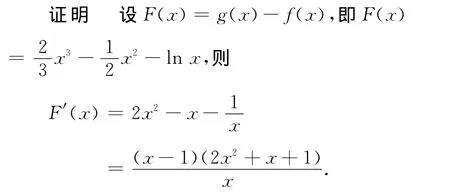
当x＞1时，

评注 函数的相关知识一直以来都是中高考，特别是高考的重点和难点，函数题目成为压轴题的情况更是屡见不鲜.而许多看似与函数无关的题目，其实都可以巧妙地通过构造函数的方法解答.构造函数之后，便涉及到函数的单调性和求导等知识的运用.因此构造函数法是另一种极为重要的解题方法.

四、构造数列

在高中阶段，常见的数列问题之一是求解数列的通项公式.常见解法主要有猜想法，累加法，累乘法以及构造新数列法.用构造法求数列的通项公式是一类广泛而复杂的问题，同时也是比较巧妙的方法.构造数列又常分为两大类：构造等比数列和等差数列，其中构造等差数列还包括一种特殊情况：构造常数列.

例7 （2012年广东高考题）设数列｛an｝的前n项和为Sn，满足2Sn=an+1-2n+1+1，n∈N＊，且a1，a2+5，a3成等差数列.

（1）求a1的值；

（2）求数列｛an｝的通项公式.

解 （1）略.

（2）将2Sn=an+1-2n+1+1与2Sn-1=an-2n+1相减，得2an=an+1-an-2n（n≥2），即是an+1=3an+2n.

验证知道n=1时也成立.

方法1 构造等比数列

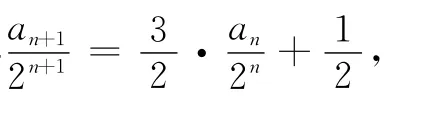
在高考中，数列问题虽不如函数占比那么大，但属于必考知识点，也是大题中的常客，甚至在某些年份的高考卷中以压轴题的身份出现（如2011年广东理科数学卷），由此足以体现命题者对其重视的程度.高中的数列以等差和等比数列为主，但数列题目中往往不会一目了然地给出这两种形式的数列，这时候就需要用到构造数列法，将题设中复杂的形式通过构造法转化成我们所熟悉的数列形式.

在如今的中学数学教学研究中，人们往往只谈“化归”而不单独讨论“构造法”，这在某种程度上讲是无可非议的，毕竟构造法是数学中一种重要的化归手段.但是不能因此减少对构造法的重视，尤其在如今数学测试的综合程度越来越高的情况下，构造法将更加频繁地应用于数学解题中，因为构造法往往能巧妙地化解许多看似无从下手的问题.但是另一方面，构造法的解题思路属于非常规思维，虽有原则可循，但却无固定的解题方法，常常需要靠学生的“顿悟”.而这其实也是对一个人创造性思维能力的一种考验［2］.同时，如今课标也越来越重视对学生创造性思维的培养，所以训练数学构造法也可以成为培养学生创造性思维的一种方式.

因此，教师在上课时可适当将构造法融入教学中，比如将其作为一题多解中的一种解法来讲解.由于构造法对解题思维的要求较高，教师最好在展示解题方法的过程中适当暴露思维过程，这样更能让学生了解解题过程中每一个步骤的由来及其使用的目的.