趣味数学融入高三复习的实践研究

况艳玲

（浙江省金华市外国语学校，321015）

面对高考的压力，高三复习教学的常见做法是压缩知识教学，进行“刷题”式训练，在一定程度上对于提高学生成绩，短期看来是有效的，但这样的复习脱离了实际，固化了学生的认识空间，使学生误以为数学就是“做题”，“学数学就是考试”.长此以往，这将导致学生对数学的感觉是疲惫和无趣的，对数学的印象单一，对数学的价值认识肤浅，对数学的精神、思想以及文化等方面体悟更少，无法陶冶学生的情操，更不能有效提高学生的综合素质.本文借助案例探索如下：

一、激发兴趣

学生学会思考，首要的是要对未知有好奇心，没有好奇心就无法激发学生探索的兴趣.在高三复习课上，有趣的数学问题能提高学生的兴趣，促使学生参与，促进学生思考.

案例1 猫吃老鼠

在复习重复排列问题时，教师经常举这样的例子：“4封信，投入3个不同的邮筒，有多少种投法？”.这样的例子过于单一，使学生感觉单调.笔者将该问题变为：“4只老鼠，3只猫，猫吃老鼠有多少种吃法（一只老鼠被一只猫吃）？”并引导学生从结果思考，因为最终的结果是“老鼠在猫的肚子里”，所以逆向思考，“猫排成一行，编号猫1，猫2，猫3，张着嘴，老鼠选择猫的肚子钻进去”.课堂上，“猫吃老鼠”的例子使学生兴趣盎然，为枯燥的复习增添几分色彩.

二、扩充知识

案例2 一元三次方程的韦达定理

例1 已知函数f（x）=（x3-6x2+3x+t）ex，t∈R.若f（x）依次在x=a，x=b，x=c（a＜b＜c）处取到极值，且a+c=2b2，求f（x）的极值点.

由f′（x）= （x3-3x2-9x+t+3）ex，可得f（x）的极值点是x3-3x2-9x+t+3=0的三根a，b，c.求解a，b，c需要用到三次方程的韦达定理.笔者类比二次方程的情形推导一元三次方程的韦达定理，类比让学生经历知识的产生和发展过程，扩大了学生的知识视野.学生提问三次函数有没有求根公式，笔者抓住契机，简要讲述了三次求根公式的发现过程——塔塔利亚、卡丹与费拉里之间的恩怨故事.课后，学生主动利用互联网了解三次求根公式的推导过程，部分学生甚至去了解一元五次方程为什么没有求根公式？这就达到了“学生课堂上带着问题去思考，课后带着好奇心去探究”的效果，扩充了学生的知识，培养了学生的探索精神.

三、探索方法

数学中许多重要的方法和概念起源于趣味数学，如哥尼斯堡问题诞生了图论与拓扑学.因此教学中应充分挖掘数学趣味题背后的数学方法.

案例3 高斯求和

高斯求和的故事广为流传，高中生几乎都知晓.在复习时，笔者认为有必要深入探索高斯求和所蕴含的方法.

图1

图2

运用类比促进学生对不同数学内容的发现与领悟，帮助学生从不同的角度记忆和理解，激发了学生自主探索新知识的热情.

二探 倒序相加的关键是通过合理的配对使某两项的和相加为定值，简化计算.

再探 倒序相加在解题中是一个重要方法，笔者利用适当的例题，让学生迁移得到一种新的方法“倒序相乘法”.

例4 （1）（tan 1°+1）（tan 44°+1）的值为_______ ；

（2）（tan 1°+1）（tan 2°+1）…（tan 44°+1）的值为_______.

本案例从趣味数学入手，充分探寻数学方法，密切关联数列、函数等重要内容，强调知识间联系的广度、深度和关联度.丰富的学习内容促使学生深度思考，促进学生批判性思维水平的提升，实现知识的意义生成和多样性价值.

四、领悟思想

趣味数学包含的思维，不仅“思维巧”，而且具有“大众性”.不同层次的学生都能参与其中，通过平等对话，相互切磋，培养了争鸣的学术意识.笔者利用趣味数学促使学生领悟数学思想，将“巧思”逐步一般化，提升学生的认知水平.

案例4 切西瓜问题

例5 如何将一个西瓜三刀切成八块？

这是一道小学趣味题，切西瓜问题可抽象为三个平面最多将空间分成8部分，由此引申出以下问题5.

例6 空间内有n个平面，设这n个平面最多将空间分成an个部分.

（1）求a1，a2，a3，a4；

（2）求an关于n的表达式.

为了回答这个问题，我们先降维，由此得到下列问题.

例7n个点最多将1条直线分成多少部分？

例8n条直线最多将1个平面分成多少部分？

笔者引导学生逐次思考：

① 先考虑“点”分“线”.

直线上n个点最多将直线分为n+1部分.

② 再考虑“线”分“面”.

记n条直线将平面最多分成bn部分，平面上1条直线将平面分成2部分，再添1条直线，该直线与原直线有1个交点，1个交点将新的直线分成2部分，这两部分都将原有的平面分成两个，所以b2=b1+2.n-1条直线将平面最多分成bn-1部分，再添1条直线，这条直线与原来n-1条直线都不平行且没有共同的交点，故有n-1个交点，n-1个交点将第n直线分成n部分，这n部分直线每一个都将原有的平面划分为二个区域，所以bn=bn-1+n，

③ 最后考虑“面”分空间.

记n个平面将空间最多分成an部分，类似“直线分平面”可得

从上述探索过程看，我们是将问题划分为不同的情形来考虑，情形之间有着密切的逻辑联系和明显的层次性差别，这种思维模式被称为爬坡思维.爬坡思维的各种情形次序不能颠倒，后者依赖前者，像爬坡一样逐级上升，每一次推理都是建立在前一步基础上的，步步上升，最终达到目标，体现从特殊到一般、从低维到高维的数学思想.

五、感悟文化

数学对文化、理性精神、现代人类思想的产生和发展有着深刻的影响.《普通高中数学课程标准（2017）》要求教师应有意识结合相应的教学内容将数学文化融入日常教学，引导学生感悟数学的价值，提升学生的科学精神、应用意识和人文素养.

案例5 河图洛书（图3）

问题 将数字1到9排成三行三列的数阵，使得无论是纵向、横向、斜向三条线上的三个数字的和都等于15.

文化背景 《易·系辞上》称：“河出图，洛出书，圣人则之”.相传上古伏羲氏时，洛阳东北孟津县境内的黄河浮出龙马，背负“河图”，献给伏羲.伏羲依此而演成八卦，后为《周易》来源.又传大禹时，洛阳西的洛宁县洛河浮出神龟，背驮“洛书”，献给大禹.大禹依此治水成功，划分天下为九州，定九章大法，治理社会.

河图洛书是中华文化的源头，在文化发展史上有着重要地位，对哲学、政治学、美学以及文学等领域有着深远的影响.复习矩阵时，笔者利用该问题和两个上古神话引入矩阵，一方面使学生有新鲜感，另一方面引导学生认识数学是一种文化，数学文化是文化的重要组成部分.学生得到答案后，笔者再给出南宋杨辉的解答“九子斜排，上下对易，左右相更，四维挺出，戴九履一，左三右七，二四为肩，六八为足”，进一步体现数学文化的丰富以及深奥.

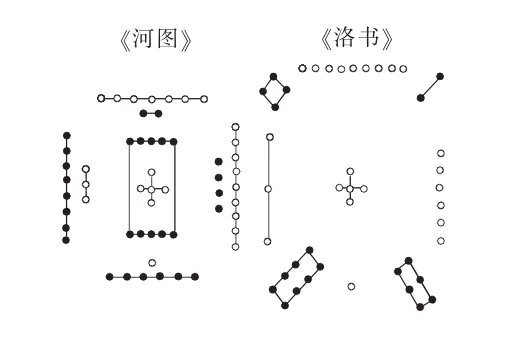
图3

六、体悟生活

在教学中运用具体、生动、形象的事例解释数学，增强学生学习数学的主动性，培养学生理论联系实际的学风.如复习选修4-4“极坐标与参数方程”时，笔者用一则故事和一则广告引入极坐标，体现数学之用.

案例6 心形曲线

一则故事 一天，一同事（语文教师）谈到“华润超市做活动，画出r=a（1-sinθ）的图像有奖品”.

一则广告 百岁山矿泉水的广告.52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀.他们相恋了，国王知道后，将笛卡尔流放.笛卡尔给克里斯汀寄出一封信，这封信内容只有一个公式：r=a（1-sinθ）.国王看不懂，将信转交给公主.公主画出图象，这就是著名的“心形线（图4）”.广告就是把百岁山的水比喻成这封另类情书，意喻“经典、浪漫、难忘、瞩目”.

图4

运用趣味数学进行复习，对教师提出了更高的要求.教师至少要做到以下三点：一是积累.积累数学趣味问题和数学史料，运用趣味数学教学的案例以及包含文化背景的高考试题；二是挖掘.挖掘趣味数学中蕴含的知识、方法和思想，挖掘其中的人文意蕴；三是思考.思考如何将趣味数学适当且有效地融入数学课堂.总之，作为一线高三教师，应该使复习的课堂充满趣味，充满思考，有方法的碰撞，有思想的交流，有文化的底蕴，最终提升学生的数学素养.