反转激发的以拍形式存在的钻柱横向振动

(东北石油大学 电子科学学院，黑龙江 大庆 163318)①

随着油田开发的深入，深层钻井技术成为了钻井领域研究的重中之重[1]。在井深不断增加的同时，一系列的问题也随之而来，最常见的就是钻柱和钻头失效[2]。在钻井作业中，钻柱长期浸泡在钻井液中，受力形式多样，从诸多案例来看，钻柱损坏事故发生率较高，造成巨大经济损失[3]。据不完全统计，中石油下属公司仅在2007年至2008年就发生钻柱失效事件637起。钻柱作为整个钻井设备的关键部分，承担起下钻头、施加钻压、传输动力等作用。由实际案例可知，钻柱的振动是造成钻柱失效的主要原因，井下钻柱振动形式分为轴向振动、横向振动和扭转振动[4]。

在钻柱振动研究初期，大部分学者认为轴向振动和扭转振动是造成钻柱失效现象的主要原因[5]。随着井下勘测技术不断发展，通过试验发现钻具下部的横向振动非常剧烈，因此，可以认为横向振动是造成钻柱失效的主要原因。钻柱横向振动会引起钻杆接头处的扭断和井底钻具组合与井壁之间的碰撞，从而导致随钻仪器的失效。在深井的研究中发现，下部钻具组合横向振动明显，但是在向上传递的过程中衰减严重，导致在地面上反映不明显。

本文研究了钻柱在受静态轴向载荷时的横向振动规律，以及由于反转运动激发的横向振动的力学模型，从钻柱所受弯曲应力角度分析了钻柱横向共振现象，说明横向振动是造成钻柱失效的主要原因。

1 反转运动

钻柱的反转运动是普遍存在的，当回转体(钻杆)以一定的速度顺时针绕自身轴线转动时，回转体与井壁之间的摩擦力造成该回转体沿井壁逆时针绕井的轴线旋转，这种运动称之为反转运动(也可以称之为反向晃振)[6]。反转的产生会立即引起相应的弯曲应力出现，当反转运动趋于稳定的时候，弯曲应力值也会趋于稳定，而且在同一井筒、同一转速下，由于反转转速变化，弯曲角频率也有差异，并且环隙比越小，反转转速越高，弯曲角频率越高，应力幅值越大。试验结果表明，沿井壁作无滑动滚动的弯曲钻柱，其弯曲角频率等于反转角频率与正转角频率之和[7]。

由于离心力作用，除钻柱上部和下部很短一段由于钻柱本身刚性没有贴至井壁外，钻杆柱各接头处均贴向井壁，如图1所示。

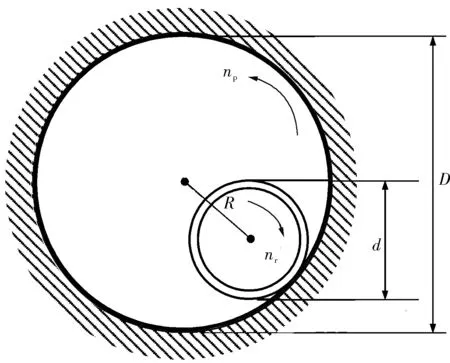
图1 钻柱反转运动示意

钻杆沿井壁做无滑动滚动时，其反转转速与自转转速呈线性关系[8]。

ωp=[d/(D-d)]ωr=βωr

(1)

np=[d/(D-d)]nr=βnr

(2)

其中：

β=d/(D-d)=d/2R

(3)

式中：d为钻杆外径，m；D为井筒直径，m；R为钻杆沿井壁反转时的半径，m；ωp为钻杆反转角速度，rad/s；np为钻杆反转转速，r/min；ωr为钻杆自转角速度，rad/s；nr为钻杆的自转转速，r/min；β为钻杆的直径与双面环隙的比值。

通过试验可知：①在钻柱运动中，钻柱的反转无论在中和点上方还是下方都会出现；②钻杆接头处的反转运动轨迹通常情况下不是圆形，它会时刻无规律的改变，而且并不总是与井壁接触，经常会出现跳离和敲击井壁的现象；③环隙比越小且转盘的转速越高，越容易出现反转运动，此时钻杆接头敲击井壁的现象越严重。

在钻杆自转转速一定时，钻杆的反转转速与环隙比有关，钻柱反转转速与转盘转速呈线性关系，但经测量后发现事实并非如此。通过不同井的参数计算分析，得到自转转速与反转转速之间的关系曲线如图2所示。图2中，实线为理论值曲线，虚线为测量值曲线。

由图2可以看出，当环隙比较小时，实际反转转速基本趋于理论反转转速；当环隙比较大时，实际的反转转速不再趋于理论计算值，说明实际情况下钻柱滚动的同时也在滑动。存在满足线性式的转盘转速值，但是当转盘转速大于该值时，反转转速小于理论值，当转盘转速小于该值时，反转转速大于理论值。这种现象可以解释为：当转盘转速小于此值时，离心力较小，钻柱出现跳离井壁的现象，缩小了钻柱绕轴线转动的回旋半径，摩擦力减小，所以反转转速高于理论值；当转盘转速大于此值时，离心力较大，增大了钻柱绕轴线转动的回旋半径，钻柱出现激烈的撞击井壁的现象，摩擦力增大，所以反转转速低于理论值[9]。

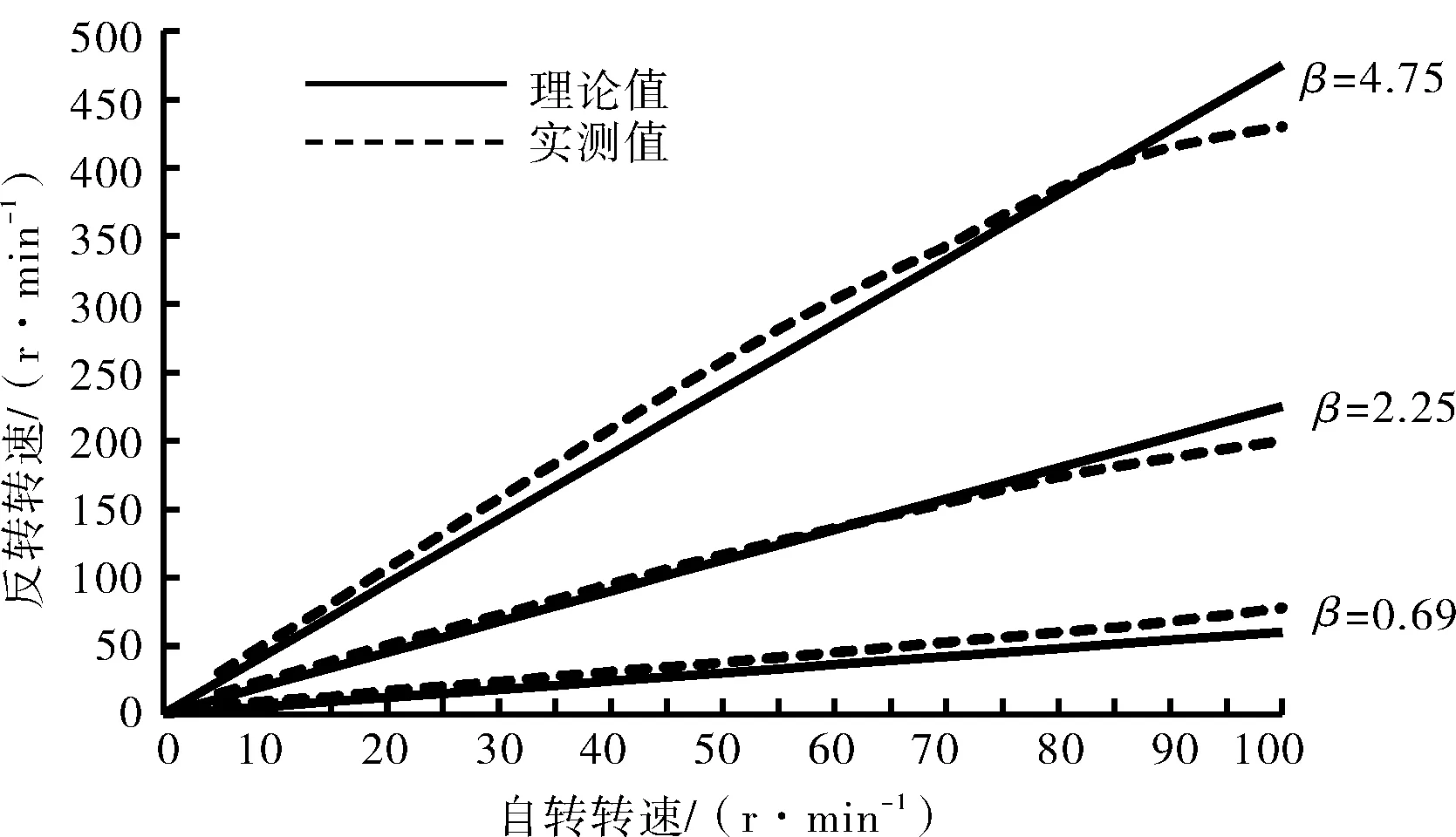
图2 自转转速与反转转速关系曲线

2 横向振动

横向振动产生的原因有很多，试验表明，反转是激发横向振动的一大因素。一般来说，由于钻杆与井壁间的摩擦力造成该钻杆沿井壁逆时针公转，这是一种自激横向振动。由于整个钻柱系统的钻杆运动方式大致相同，故可以简化为从研究一个单元入手去研究钻柱的横向振动[10]。

以大庆油田升深7井为例，其参数如表1所示。

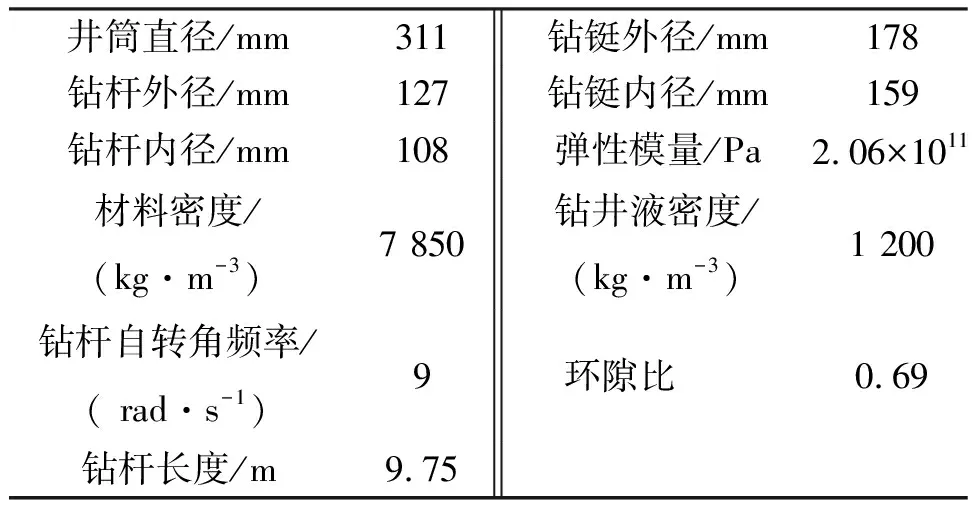
表1 大庆油田升深7井参数

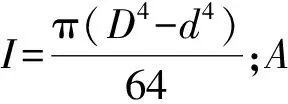
图3 钻柱横向振动力学模型

对发生横向振动的钻柱做出如下假设：①忽略阻尼影响；②井筒只对两端接头有约束；③只考虑轴向力作用；④固定两端边界条件。

此时微元段的动能为

(4)

所取钻杆的总动能为

(5)

此时微元段的势能为

(6)

所取钻杆的总势能为

(7)

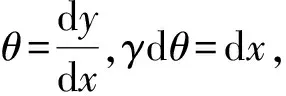
根据M/I=E/γ，由Tmax=Vmax可得：

(8)

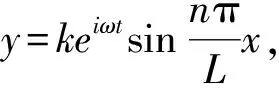
(9)

研究发现，钻柱横向振动固有频率不仅与钻柱本身的性质有关，钻柱所受的轴向静态载荷对横振固有频率也会产生很大的影响[11]。

所取微元段所受静态轴向载荷为发生横向振动部位以下的钻杆的重力减去浮力[12]，则静态载荷为

(10)

式中：x1为横向振动部位与中和点之间的距离，m；A1为钻铤的横截面积，m2；h为中和点以上钻铤的长度，设为25 m；ρ1为钻井液密度。

在静态轴向载荷作用下的钻柱的横向振动方程为

(11)

钻柱横向振动固有角频率为

(12)

通过式(12)分析可知，中和点以上钻柱所受的轴向力为拉力作用T>0，拉力使横振固有频率增大，中和点以下钻柱所受的轴向力为压力作用T<0，压力使横振固有频率减小。

不同部位与数量钻杆的横向振动固有角频率(一阶振动，n=1)如表2。

表2 不同部位与数量钻杆的横向振动固有角频率(一阶振动，n=1)

由表2可知，单根钻柱时的实际振动频率很难达到钻柱横向振动固有频率，故可以认为单根钻柱并无横向共振；振动部位距中和点距离一定时，钻杆长度越长，钻柱横向振动固有角频率越小；钻杆长度一定时，振动部位距离中和点距离越近，钻柱横向振动固有角频率越小。

3 横向振动中拍的现象

由于钻杆本体直径小于接头外径，所以该处引起的横向振动角频率低于两端接头处的横振角频率。在钻柱运动过程中钻杆接头在小环隙时不规则地跳离井壁，以及钻杆有初始弯曲，以及相邻接头运动的相互影响等，都会造成各钻杆接头反转转速不稳定。因此大多数情况下钻柱的横向振动会以拍的形式表现出来。

这种现象，可用位移时间图来说明。当两个同方向、不同频率的简谐运动合成时，由于这两个相差很小分振动频率，因而它们的相位差随时间改变，合振动一般不再是简谐运动，其合振的振幅时而加强，时而减弱的现象叫做拍[13]。可简单假设，两简谐运动的振幅分别为A1和A2(A1=A2)，初相分别为φ1和φ2，角频率分别为ω1和ω2，且ω1<ω2。

设A2=A1，初相均为零，其运动方程分别为

x1=A1cosω1t=A1cos2πv1t

(13)

x2=A2cosω2t=A2cos2πv2t

(14)

合振动位移为

x=x1+x2=A1cos2πv1t+A2cos2πv2t

(15)

已知，振幅相同，故合振运动方程为

(16)

以大庆油田升深7井距离中和点1 000 m处合振动为例，当取两根钻柱时，用MATLAB获得其波形图如图4所示[14-15]。

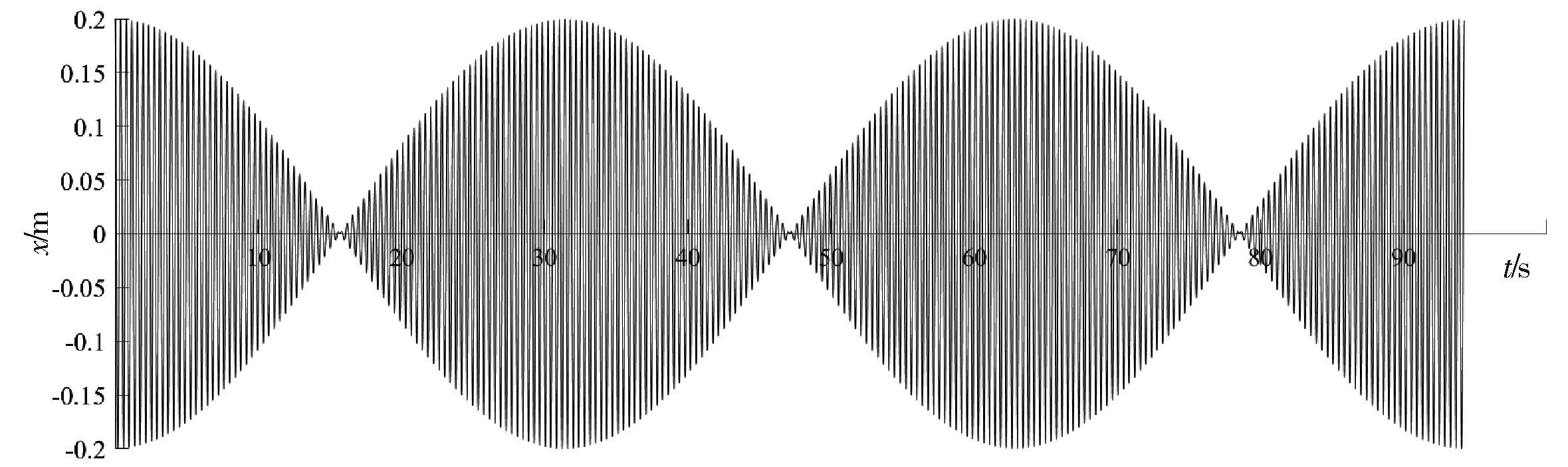
图4 升深7井合振动时间位移

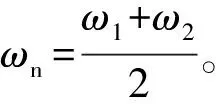
4 最大挠度计算

反转运动引起的弯曲应力造成了钻柱的横向振动，故可以通过最大弯曲挠度来分析横向振动。

1) 考虑单一反转的情况。由于两端固定，假设单根的钻柱是一个某一瞬间处于力平衡状态的简支梁，并已知其中点的最大挠度。在该钻柱上作用了2种载荷，一是由于偏心半径引起的离心载荷，二是单根钻杆产生正弦状弯曲变形而引起的正弦分布载荷[15]。按照材料力学，钻杆的最大弯曲挠度为

(17)

式中：ωn为钻杆的横向振动固有频率。

(18)

在只考虑反转的情况下，当反转运动角频率与该钻杆固有角频率相等时，钻柱发生共振，钻杆中部的挠度和弯曲应力会急剧增高。

2) 考虑既有反转也有自转的情况。与单一反转不同的情况是，正弦分布载荷是由角速度ωp+ωr引起的[16-17]。最大挠度为

(19)

所以，当弯曲应力波叠加处的反转角频率与自转角频率之和等于此处的钻柱横振固有角频率时，钻柱会发生共振。

以大庆油田升深7井为例，研究钻柱既有反转也有自转的情况，结合钻杆的固有横振角频率，可获得数据如表3所示。

表3 距中和点不同距离处横振固有角频率与最大挠度

从表3中可以看出，在钻柱所受静态轴向载荷由拉力作用时，中和点作为能量陷落点，距中和点越远，越接近井口处时，钻柱所受拉力越大，横振固有角频率越大。以大庆油田升深7井为例，当钻柱自转角频率达到85 r/min时，振动部位距中和点1 000 m的横向振动角频率达到15.21 rad/s，此时钻柱振动角频率接近横向振动固有角频率，容易发生共振现象。在钻井过程中，可以通过调节钻柱的自转转速或者使用加厚钻杆来有效的规避钻柱横向共振。

5 结论

1) 当环隙比小于2.25时，反转转速与自转转速呈线性关系，由此可将反转转速控制在合理范围内。

2) 钻柱的横向振动固有频率与钻柱所受静态轴向载荷有关。在中和点以上，钻柱所受静态轴向载荷为拉力，钻柱横向振动固有频率增大；在中和点以下，钻柱所受静态轴向载荷为压力，钻柱横向振动固有频率减小。

3) 反转引起的弯曲应力波沿钻杆传递，所以拍的现象遍布于整个钻杆上。钻柱的横向振动大都以拍的形式合理的表现出来。由合振动运动规律可知，钻柱的横向振动固有角频率也可以用拍现象叠加后的合振角频率表示。

4) 当合振角频率接近钻柱反转角频率与钻柱自转角频率之和时，则发生横向共振。当合振角频率与钻柱反转角频率与钻柱自转角频率之和相差较大时，可求出钻柱的最大弯曲挠度。