基于模糊控制的自适应虚拟同步发电机控制策略

周建萍，胡成奕，茅大钧，邓玉君，叶剑桥，方乐

(上海电力大学 自动化工程学院，上海 200090)

随着新能源的不断发展，电力系统规模日益壮大[1-4]。大多数新能源发电设备通过电力电子接口电路连接到电网，而逆变器接口的低惯性和无阻尼特性将对系统的稳定运行产生负面影响。

虚拟同步发电机(virtual synchronous generator，VSG)的概念最初由荷兰学者在VSYNC项目中提出[5]。当功率不平衡时，VSG可通过调节虚拟惯量和阻尼系数来抑制其自身频率和功率的波动，并在一定程度上抑制系统振荡；因此，灵活调整虚拟惯量和阻尼系数是研究的关键。结合同步发电机的振荡方程，文献[6]提出一种具有交变虚拟惯量的VSG。文献[7]通过分析VSG的角频率变化率及功角曲线，提出一种可变虚拟惯量的VSG控制策略。为克服上述固定虚拟惯量、交变惯量和可变惯量的缺点，文献[8]推导了自适应虚拟惯量的修正表达式。

以往研究主要集中在从VSG可控虚拟惯量的角度来削弱系统的振荡。实际上，阻尼系数对改善暂态响应也有显著影响，文献[9]研究使用VSG技术进行分布式发电的阻尼振荡方法。文献[10-11]提出一种基于VSG的虚拟惯性和阻尼协调自适应控制方法，但没有明确控制变量系数和优化模型边界条件阈值的选择原则，当参数选择不够理想时易影响控制结果。文献[12]根据小信号分析法得到虚拟惯量与阻尼系数和VSG频率绝对值变化率之间的关系式，但忽略了频率偏差的影响。文献[13-14]同时分析了角频率偏差、角频率变化率与虚拟惯量、阻尼系数之间的关系，但未考虑当扰动到达临界振荡时的情况。

为此，有相关文献提出使用模糊控制进行参数自适应调节。文献[15-18]采用模糊控制实现对VSG虚拟惯量的自适应调整，在系统扰动较小时，相较于其他自适应虚拟惯量控制方法更有效，但未考虑阻尼系数的影响。

为了对以上2个虚拟参数进行综合分析，本文提出一种基于模糊算法的VSG控制策略，可灵活调整虚拟惯量和阻尼系数。首先，VSG的控制原理参考同步发电机的转子运动方程和无功电压方程。然后，在VSG功角曲线进一步划分的各个区间内，通过分析同步发电机的虚拟惯量、阻尼系数与角频率偏差、角频率变化率之间的关系，设计模糊规则表，采用模糊算法实时控制虚拟惯量和阻尼系数的变化。最后，在MATLAB/Simulink仿真平台上构建自适应VSG控制模型，对该控制方法的有效性和优越性进行验证。

1 VSG控制策略

1.1 VSG控制原理

本文提出的自适应VSG控制策略的系统结构如图1所示，其中：Udc为直流侧电压；LC滤波器由电感(其值为Lf)和电容(其值为C)组成，Rf为滤波电阻；ifabc为逆变器输出电流，ifdq为其旋转坐标系下的分量；Lg为电网侧电感；uabc和iabc为滤波输出电压、电流，udq和idq分别为其旋转坐标系下的分量，二者经过功率计算得到有功功率P和无功功率Q；将有功功率、无功功率设定值Pref和Qref输入至VSG控制模块进行电网功率调控，输出VSG的虚拟电势幅值Em和相位θ，构成参考电势eabc，edq为其旋转坐标系下的分量；Δω为角频率偏差；dω/dt为角频率变化率；ΔJ为虚拟惯量的调节量；ΔD为阻尼系数的调节量。由于在远距离传输中线路电感远大于线路电阻，故忽略线路电阻。

首先，该控制结构模拟磁极对数为1的同步发电机模型，VSG的虚拟转子运动方程如式(1)所示，且VSG的电磁角速度等于机械角速度[11]。

(1)

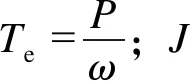
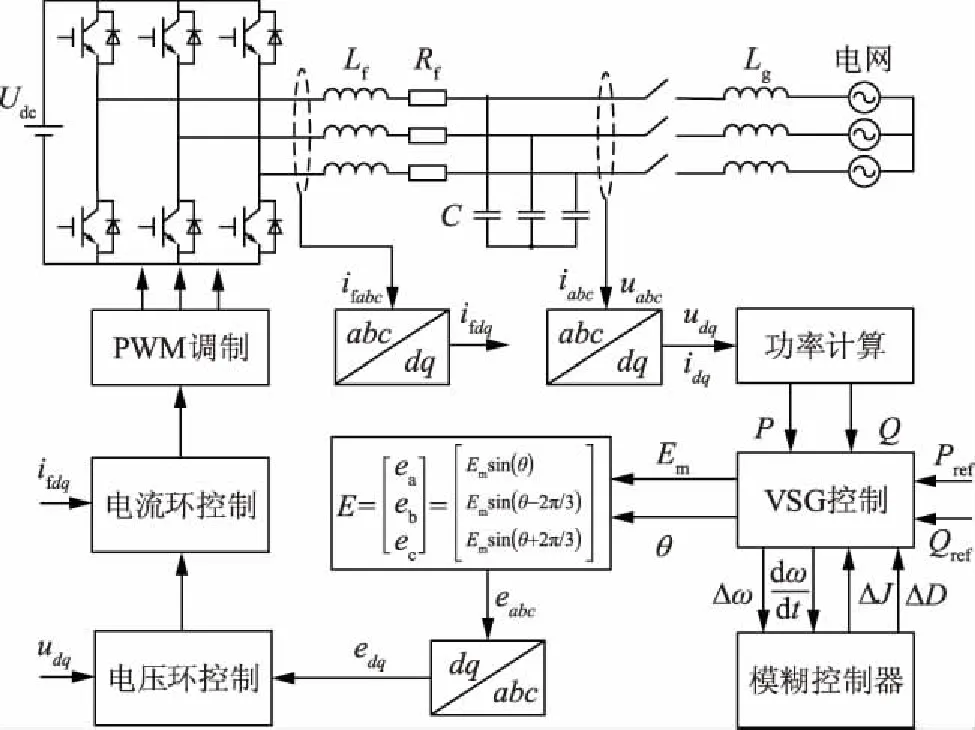
图1 VSG控制策略的系统结构Fig.1 System structure of VSG control strategy

其次，模拟同步发电机调节励磁的过程，以调节VSG中的虚拟电势Em。

Em=E0+ΔE，

(2)

(3)

式中：E0为VSG的空载电势；Q为无功功率实际值；Uref和U分别为VSG端电压的额定值和实际值；kq和kv分别为无功功率调节系数和电压调节系数。

图2 VSG控制的有功环和无功环Fig.2 Active and reactive power loops of VSG control

1.2 虚拟参数整定

参考文献[19]的相关方法，并根据VSG输出的有功和无功功率表达式，可得到自然振荡角频率ωn和阻尼比ξ：

(4)

式中SE为同步功率的标幺值。

此时，VSG特征根

(5)

2个闭环特征根均位于左半平面，在此基础上的一定范围内调节虚拟惯量和阻尼系数的大小，能保证系统的稳定性。

2 模糊控制器

2.1 模糊变量分析

通过分析VSG的模型，式(1)可以变换为：

(6)

(7)

若式(6)中dω/dt恒定，则可通过增加阻尼系数D来减小角频率偏差Δω；若式(7)中Td恒定，则可通过增加虚拟惯量J来减小角频率变化率dω/dt。然而，同时调节J和D来控制角频率偏差和角频率变化率可更大程度地保证频率稳定性。

VSG的功角曲线和角频率振荡曲线如图3所示。当有功出力从P1转变到P2时，系统的稳定工作点将从点a切换到点c，且功率和角频率的变化都是阻尼振荡的过程。由于每个区间内功率和角频率变化具有不同趋势，虚拟惯量和阻尼系数也将随之变化。

表1总结了在各个时间间隔内虚拟参数的变化趋势。大部分文献将振荡周期分为4个区间[13-14]，为了能在振荡过程中更准确地反映有功功率和角频率的变化，本文将区间进一步细分并进行如下改进：区间1和2的角频率偏差和角频率变化率均为正，

图3 VSG的模拟功角曲线和角频率振荡曲线Fig.3 Power angle curves and angular frequency oscillation curves of synchronous generator

但区间1的角频率偏差小于区间2的角频率偏差，区间1的角频率变化率大于区间2的角频率变化率；当振荡到达区间3时，角频率变化率为0；当振荡到达区间6时，角频率偏差为0，处于临界振荡，若此时角频率变化率不为0，仍然需要调节虚拟参数；同理，区间7和8的角频率偏差和角频率变化率均为负，但区间7的角频率偏差小于区间8的角频率偏差，区间8的角频率变化率大于区间7的角频率变化率。

表1 J和D的控制规律Tab.1 Control laws of J and D

在区间1中，由于输出角频率大于电网参考角频率，但角频率偏差值不大，因此需要适当增加虚拟惯量且增加阻尼系数以约束角频率的增加。在区间2中，角频率仍然大于电网参考角频率，但此时角频率变化率缓慢减小，因此持续增加虚拟惯量和阻尼系数进一步约束角频率的增加。直到区间5之前，VSG角频率变化进入减速状态，可适当减小虚拟惯量。在区间6中，输出角频率与电网参考频率相同，处于临界振荡，因此将虚拟惯量和阻尼系数恢复至初始值，并继续监测角频率变化率。以此类推，在后续区间中需要不同的虚拟惯量。随着VSG角频率的变化幅度减小，所需阻尼系数也随之减小并恢复到初始值，直到系统逐渐稳定。然而，区间不应划分得过于精细，否则在模糊过程中易缺失数据，并增加算法推理工作量。

2.2 模糊控制器设计

为了提高电网频率的精确控制，本节提出了一种基于模糊算法的自适应VSG控制策略，根据角频率的变化情况实时调节虚拟惯量和阻尼系数。

模糊控制器主要由模糊化，模糊推理和去模糊化组成，如图4所示，其中k1、k2为量化因子。

图4 模糊控制器结构
Fig.4 Fuzzy controller structure

a)模糊控制器提取角频率偏差Δω和角频率变化率dω/dt，具体输入变量如下：

(8)

b)通过模糊化将精确的输入值变为模糊值。使用量化因子对输入信号进行归一化处理[15]，量化因子k1=10，k2=1/100。

c)模糊控制器通过给定的模糊规则和去模糊化推理得到虚拟惯量ΔJ和阻尼系数ΔD。

d)通过式(9)获得实时虚拟参数：

(9)

式中J0、D0分别为J、D的初始值。

在模糊逻辑控制器中采用三角(trimf)隶属函数和梯形(trapmf)隶属函数。角频率偏差和角频率变化率的基本论域都设置为[-1,1]，虚拟惯量变化范围设置为[-0.1,0.1]，阻尼系数变化范围设置为[-5,5]。在对输入、输出信号进行量化之后，将输入量和输出量分别映射到相应的区间，对应模糊变量的集合范围是{负大(NL)，负小(NS)，零(ZO)，正小(PS)，加大(PL)}。相关隶属度函数如图5所示。

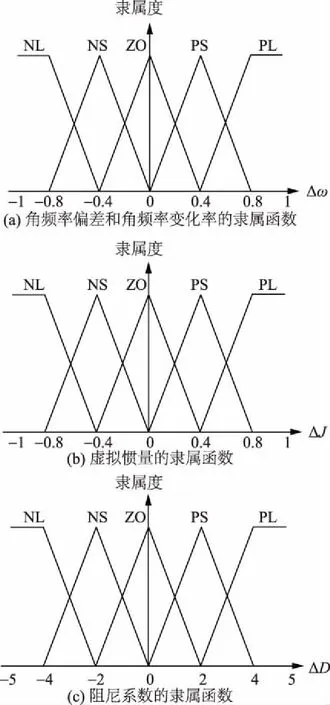
图5 输入和输出变量的隶属函数Fig.5 Membership functions of input signal and output signal

本文设计的模糊规则见表2和表3。由于输入确定，因此通过MAX-MIN方法推算得到输出模糊控制量。

表2 J的模糊规则Tab.2 Fuzzy rules of J

模糊控制的非线性优势在于：无需在控制中构建复杂的数学模型，并且具有灵活的适应能力。

2.3 模糊控制VSG

基于VSG控制的逆变器主要通过电压、电流双环控制产生PWM调制信号。

表3 D的模糊规则Tab.2 Fuzzy rules of D

如图2所示，在有功环中，模糊控制主要用于实时调节虚拟惯量J和阻尼系数D，进而实时调节虚拟电势的相位θ；在无功环中，通过比较逆变器输出电压U和参考值Uref，比较输出无功Q和参考值Qref，乘以各自的调节系数，进而得到虚拟电势的幅值Em。

图6 电压、电流双环控制Fig.6 Voltage and current double loop control

由此可见，根据角频率偏差和角频率变化率制订相应的模糊规则，实时调节虚拟惯量和阻尼系数的变化量，跟踪角频率ω的变化，以确定VSG输出参考电压的相位θ，可减小参考电压的畸变程度，从而减小并网点处谐波电流含量，提高VSG控制下的电能质量。

3 仿真与分析

3.1 仿真条件

为验证所提出的基于模糊算法的自适应VSG控制具有更好的动态响应能力，本文在MATLAB/Simulink平台搭建如图1所示的仿真结构并进行测试。比较了文献[10]自适应虚拟惯量与阻尼系数控制、文献[17]基于模糊算法的自适应虚拟惯量控制和本文基于模糊算法的自适应虚拟惯量与阻尼系数控制的仿真结果。主要仿真参数见表4。

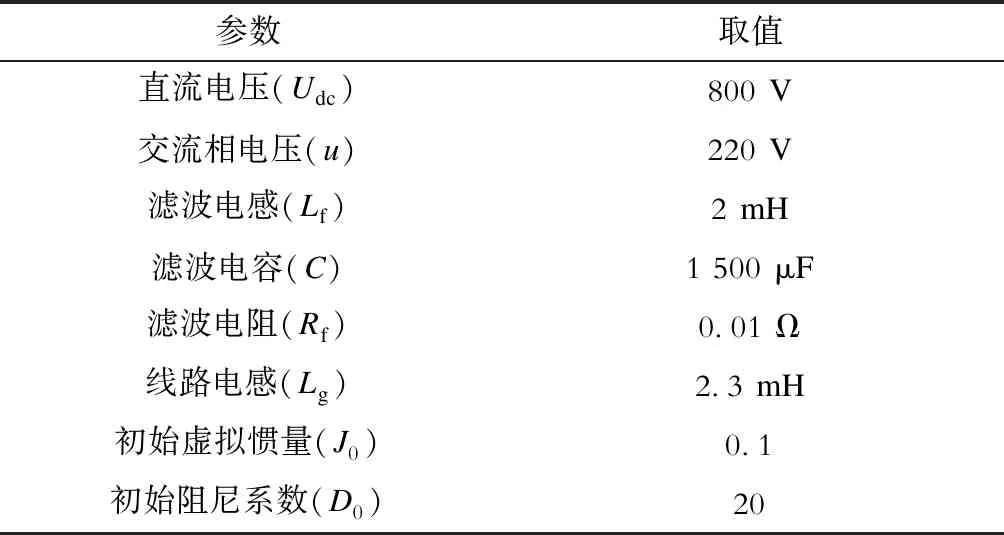
表4 主要参数Tab.4 Main parameters

仿真时长设置为1 s。仿真开始时，设置VSG输入有功出力为5 kW，无功出力为5 kvar。t=0.4 s时，有功功率突然增加至10 kW；t=0.7 s时，有功功率从10 kW降低至5 kW。考虑到系统启动时的状态不在模糊控制的执行范围内，模糊控制器在t=0.1 s时启动。

3.2 仿真结果比较

图 7和图8分别给出了上述3种控制方式下的VSG有功功率和频率的变化情况。

a)工况1：系统输入有功功率突增。

在系统启动0.1 s后，VSG输出有功功率由0增加至5 kW，采用基于模糊算法的自适应虚拟惯量控制方法时，暂态过程中有功功率出现严重超调，角频率也出现超调，且需要经过约0.2 s的振荡过程才能达到稳定；采用自适应虚拟惯量和阻尼系数控制方法时，暂态过程中有功功率振幅较大；采用本文提出的基于模糊算法的自适应虚拟惯量和阻尼系数控制策略时，暂态过程中有功功率变化平稳，角频率的波动限制在±1 rad/s范围内，瞬态过程也仅持续约0.1 s。

系统进入稳定运行状态，当输入有功功率由初始5 kW突增至10 kW，采用自适应虚拟惯量和阻尼系数控制方法或基于模糊算法的自适应虚拟惯量控制方法时，暂态过程中有功功率的振荡幅度有所减弱，其中：采用基于模糊算法的自适应虚拟惯量控制方法时，角频率波动变化较大；采用自适应虚拟惯量和阻尼系数控制方法时，角频率波动减小，但振荡持续时间仍持续约为0.2 s。采用本文提出的基于模糊算法的自适应虚拟参数控制策略时，角频率振荡时间约为0.1 s。

b)工况2：系统输入有功功率突降。

当输入有功功率由10 kW突降至5 kW时，进一步分析暂态过程的角频率变化情况，若采用本文提出的基于模糊算法的自适应虚拟参数控制策略，相较于自适应虚拟惯量和阻尼系数控制方法，能更快速响应，响应时间约为0.01 s。

另外，无功功率的变化主要受虚拟励磁系数的影响。

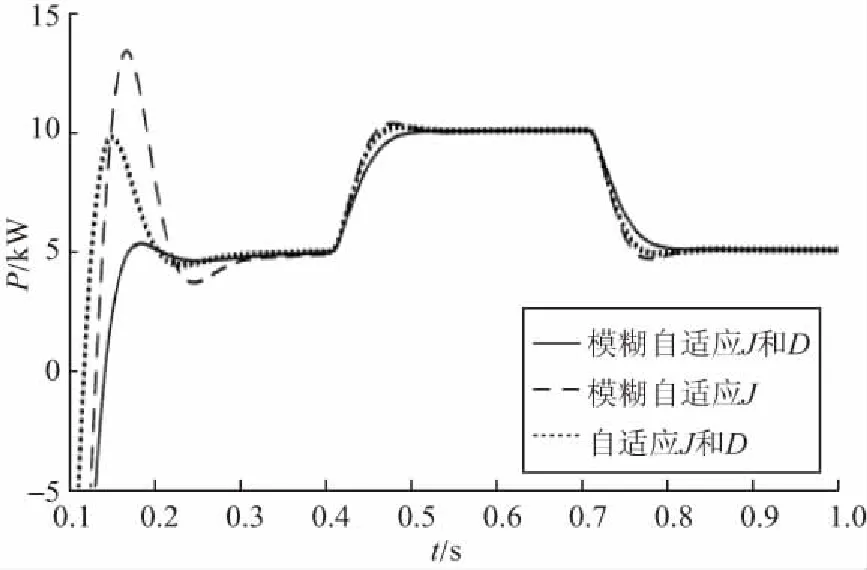
图7 VSG输出有功功率Fig.7 Output active power of VSG

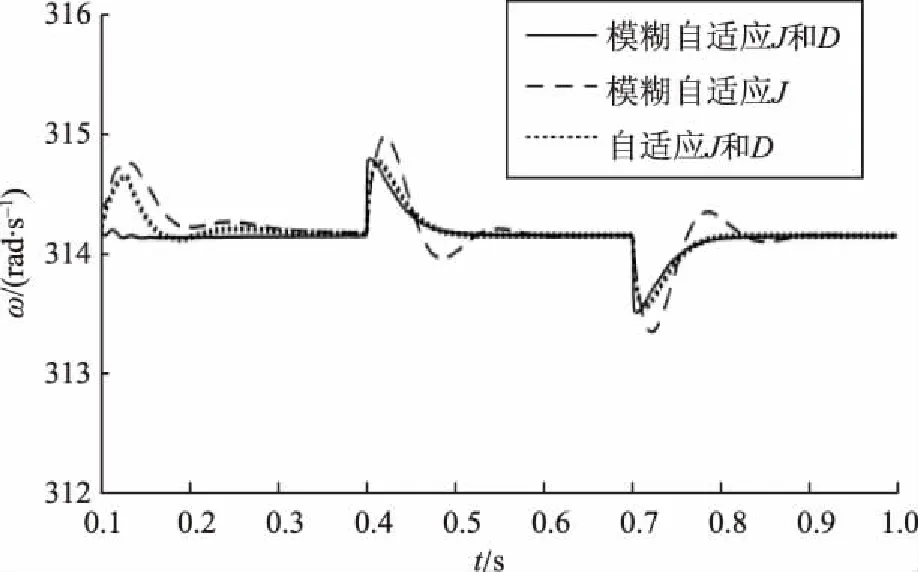
图8 VSG角频率Fig.8 Angular frequency of VSG

在t=0.1 s时截取系统FFT分析结果。当采用基于模糊控制的自适应虚拟惯量与阻尼系数控制策略时，如图9所示，并网点电流总谐波畸变率(total harmonic distortion，THD)仅为0.81%。当给定有功功率突增或突降时，该控制方式下的谐波含量较低，能够改善电能质量，从而维持电网的稳定运行。

基波幅值(50 Hz)为14.02，THD为0.81%。

图9 并网点电流FFT分析
Fig.9 FFT analysis of grid-connected current

图10和图11为暂态过程中自适应调节的虚拟参数变化。可以看出，当有功功率突然增大时，角频率增大；因此VSG的虚拟惯量迅速增大，加速了系统变化的加速度，阻尼系数也增大，协调抑制系统振荡。

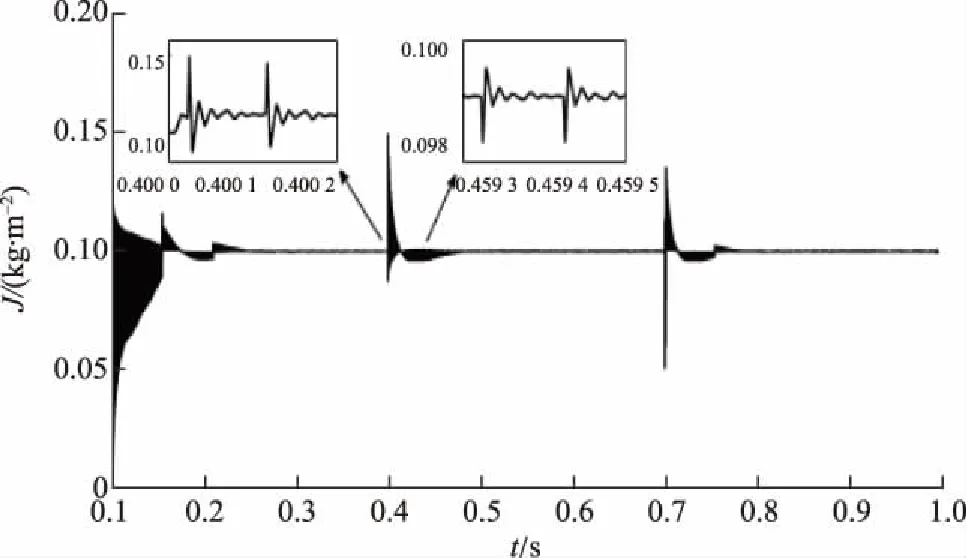
图10 自适应虚拟惯量变化Fig.10 Adaptive variable virtual inertia

图11 自适应阻尼系数变化Fig.11 Adaptive variable damping coefficient

另外，从局部放大图(t=0.400 0 s至t=0.400 2 s)看出，在系统加速变化的过程中，虚拟惯量和阻尼系数在模糊控制下处于波动状态，且振幅在逐渐减小，整体呈现下降趋势，随着角频率逐渐步入稳态值，虚拟惯量和阻尼系数也恢复至初始值。从局部放大图(t=0.459 3 s至t=0.459 5 s)可看出，由于角频率的变化率不为零，虚拟惯量的变化量为负值且缓慢减小，继续反方向抑制角频率振荡，而此时角频率振荡幅度减弱；因此阻尼系数保持在初始值状态，系统开始减速并迅速进入稳定状态。

从仿真结果可以看出，采用本文提出的策略时，系统可根据扰动自适应调节VSG的虚拟惯量和阻尼系数，从而显著提高动态响应特性和系统运行稳定性。

4 结论

随着新能源的发展，分布式发电装置的输出波动可能在暂态过程中引起频率和输出功率的长期振荡。如果振荡超出安全运行阈值，将不利于系统的稳定运行[20-25]。因此，本文提出一种基于模糊算法的参数自适应调节VSG控制策略，得出如下结论：

a)通过模拟同步发电机的转子运动方程推导出VSG控制方法，进一步分析了虚拟惯量和阻尼系数对VSG控制性能的影响，验证了这2个虚拟参数在系统动态运行中的协调控制效应。

b)在动态过程中将角频率响应曲线划分为更详细的区间，并根据角频率变化率和角频率偏差的变化趋势，给出各区间对应的虚拟惯量和阻尼系数的变化规律，重新设计模糊控制器。模糊控制可实时调整虚拟参数，达到快速响应，减少超调，从而提高动态响应性能。

c)基于模糊算法的自适应VSG控制策略能在一定程度上减少并网点处谐波含量，维持系统安全稳定运行。