基于分体解耦方法的变压器温度场模拟

张建瓴，周壮广，可欣荣

(华南农业大学 工程学院，广东 广州 510642)

油浸式电力变压器绕组热点的数值和位置计算对变压器的优化设计和可靠运行具有重要意义[1]。目前对变压器热点和温度场的计算方法主要有数值计算法和热路法[2-3]，其中，热路法使用热电类比模型，以顶层油温为主要参考依据来计算热点温度；数值方法〔如有限元法(finite element method，FEM)、有限体积法(finite volume method，FVM)、间断伽辽金法(discontinuous Galerkin method，DGM)等〕使用整体模型和简化模型。前者在场方程的计算域中包括变压器的散热器与油箱内部，后者的计算域只考虑油箱内部。

文献[4-5]使用FEM计算油浸式电力变压器温度场分布时采用简化模型，直接给定油箱入口处的油温和油速，并在出口处直接导出油流和热量。文献[6-10]采用FVM计算变压器温度场时同样以固定的入口油温作为边界条件进行分析；采用简化模型的数值方法计算简单方便，但误差较大，特别是将入口油温假设为接近环境温度的恒定值时，误差明显增加。文献[11-12]在使用FVM时采用整体模型，在数值计算域中同时考虑多组散热器和油箱内部。文献[13]在使用DGM时采用整体模型，计算得到的热点温度与实测值误差较小。对于广泛使用的片式散热器，因所用散热器组数多，单组片数较多且片体较薄，采用整体模型的数值方法在网格剖分时需要复杂的剖分技巧以及更精细的网格划分，使得网格数量大幅增大，计算迭代次数增加且收敛性较差。

为了解决整体模型计算复杂度和简化模型误差水平之间的矛盾，本文提出一种分体解耦方法，并以S9-1600/10/0.4型变压器温度场模拟为例，将散热器与油箱内部分离，对物理场计算进行解耦，同时提出一种油箱和散热器出入口油温互约束模型来描述温度场计算中散热器与油箱内部的耦合关系。具体计算中，首先使用Comsol软件建立散热器组的仿真模型，得到散热器出口油温和入口油温、油速的关系，以及油箱和散热器出入口油温的互约束关系式；然后在油箱温度场计算中不再对多个散热器组进行剖分模拟，而是直接使用前述关系式。该方法计及了散热器对流和辐射散热作用，在保证计算准确性的同时明显提高了计算效率。

1 变压器涡流场及损耗计算

变压器运行过程中，绕组、铁心和夹件等结构件的损耗是变压器的主要热源，直接影响变压器的温度分布[14]。使用A-V-A方法[15-16]计算变压器的涡流场时，在复频域中，铁心、夹件和油箱为导电涡流区，绕组和变压器油为非涡流区。各计算域的控制方程如下[17]：

涡流区

(1)

变压器油

×μ-1(×A)=0;

(2)

绕组

×μ-1(×A)=Je.

(3)

式中：μ为磁导率，H/m；σ为电导率，S/m；ω为角频率，rad/s；Je为线圈电流密度，A/m2；A为矢量磁位，Wb/m；V为标量电位，V。

铁心采用均匀化材料模型，设y轴垂直于硅钢片轧制方向，x和z轴沿硅钢片轧制方向，则等效电导率及磁导率张量[18-19]分别为：

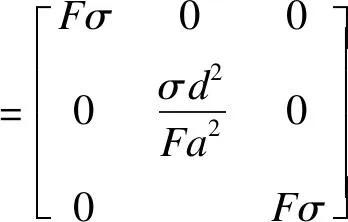
(4)

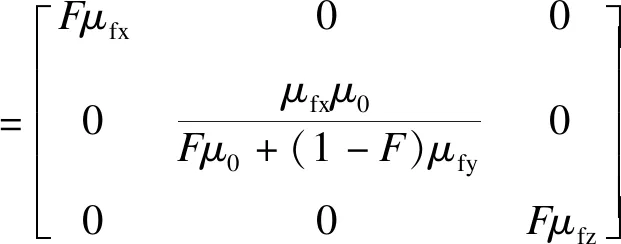
(5)

式中：F为铁心叠积系数；a为叠片宽度，mm；d为叠片厚度，mm；μfx、μfy和μfz为分别为沿x、y和z方向的磁导率，H/m；μ0为真空磁导率，H/m。

仿真计算时，采用A-V-A法计算变压器的漏磁场，得到各结构件的体积损耗密度分布后，再积分得到绕组、铁心和夹件的损耗，计算结果见表1，以此得到各结构件的发热功率。

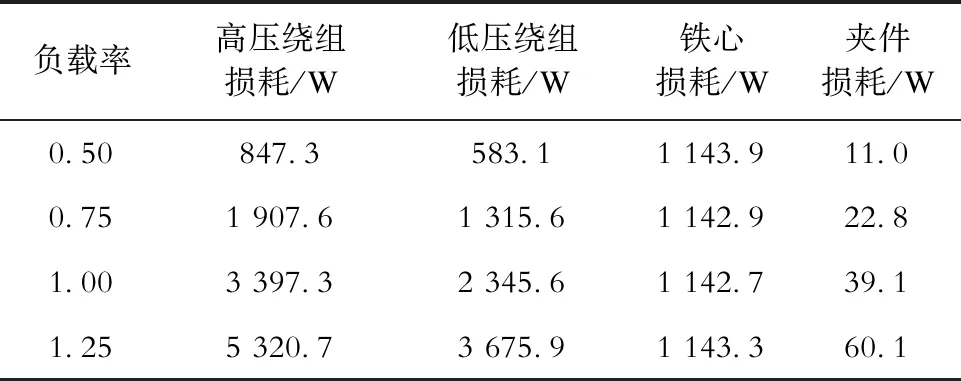
表1 各结构件损耗计算结果Tab.1 Calculation results of loss of transformer structural parts

2 散热器温度特性计算

2.1 散热器材料模型及网格划分

根据文献[20]和S9-1600/10/0.4型变压器的容量和实际尺寸、参数，选取可拆卸式片式散热器组成6个散热器组，前后对称布置，每边并列安装3个。忽略散热器的壁厚影响，建立单个散热器组的几何模型，模型中主要材料为变压器油，油道之间由隔离体相互隔绝，隔离体使用合金钢。变压器材料物性参数见表2。

对单个片式散热器组采用物理场控制网格进行剖分，单元尺寸为常规。网格单元总数为1 204 839，平均单元质量为0.527 1。

表2 变压器材料物性参数Tab.2 Physical property parameters of transformer material

注：T为变压器油温度。

2.2 流体传热模型

流体稳态对流传热的物理场方程可表示为

ρCpu·T+·(-λT)=Q.

(6)

式中：r为材料密度，kg/m3；Cp为恒压热容，J/(kg·K)；u为流体速度场，m/s；λ为导热系数，W/(m·K)；Q为热源，W/m3；T为温度场变量，K。仿真计算时，油为流体传热，隔离体为固体传热。式(6)中当u为0时即为固体的热传导方程。

散热器热量散失的主要途径为对流和辐射散热。对流散热时，散热器外表面设置为传热学第3类边界条件，对流换热系数在自然对流时取10，在强制风冷时取20[12]；辐射散热时主要考虑散热器外表面对环境的辐射，忽略其内部表面的热辐射，表面辐射率取为0.9。散热器对流和辐射散热计算时，环境温度取293.15 K(摄氏温度20 ℃)，入口油温可预先设定，出口热流为自由流出。

将变压器油的流动简化为不可压缩层流，流体的动量方程和质量方程为[21]

(7)

式中：p为油的压力，Pa；rref为参考密度，kg/m3；g为重力加速度，m/s2；I为单位张量。流体的能量方程退化为对流传热方程式(6)。

模拟计算时，使用P1+P1分段线性插值对流体进行离散化处理。壁面无滑移，设置散热器入口油速(指入口处油的法向速度，以下同)，散热器出口处使用压力边界条件[22]，并在多物理场模块中设置温度耦合和流动耦合。

2.3 散热器温度计算结果及分析

假设变压器6个散热器组的降温效果相同，取其中1个进行模拟。以散热器组入口油温和油速为控制变量，分别考虑自然对流和强制风冷2种情况进行计算。

图 1所示为自然对流情况下，散热器组入口油温为348.15 K、油速为0.05 m/s时集油管、散热器组入口处第1片单元盒和单个散热器组的温度分布。由图1(c)可知，散热器组的温度从上到下逐渐降低，散热器组的出口油温为335.59 K，出入口油温相差12.56 K；集油管上表面的散热条件较好，其温度比下表面低〔如图1(a)〕；油流通过油道后汇集于下集油管中，因中间油道受到两边油道的热相互作用，中间油道的油温高于两边油道油温〔如图1(b)〕。

图1 散热器温度分布Fig.1 Radiator temperature distribution

图2和3分别为自然对流冷却和强制风冷2种情况下不同入口油速时，散热器出入口油温的关系曲线。由图2和3可以看出，当散热器入口油速vrin一定时，自然对流冷却和强制风冷2种情况下散热器的出口油温Trout与入口油温Trin均近似为线性关系，即

Trout=kTrin+b.

(8)

式中斜率k和截距b只与油速vrin有关，k值反映了降温效率，k值越大，散热器出口油温越高，降温效果越差，反之，k值越小，降温效果越好。当散热器的入口油温一定时，入口油速越大，出口油温越高。但随着散热器入口油速增大，同一入口油温时散热器出口油温增加变缓，即k值增加程度变小并逐渐趋于一个极限值。

图2 自然对流时散热器出入口温度特性Fig.2 Relationship between oil temperatures at radiator outlet and inlet in natural convection condition

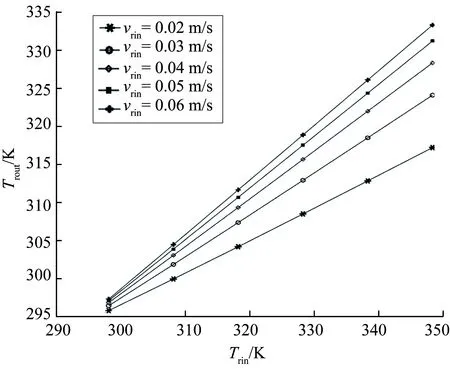
图3 强制风冷时散热器出入口温度特性Fig.3 Relationship between oil temperatures at radiator outlet and inlet in forced air-cooling condition

为了进一步探讨散热器出口油温与入口油温、油速的关系，在图2和图3中针对不同入口油速下的k值和b值进行拟合，自然对流时有

(9)

式中k(vrin)和b(vrin)表示k和b为vrin的函数。

强制风冷时有

(10)

根据式(7)、(8)可以将散热器出口油温与入口油温、油速的关系统一为

Trout=k(vrin)Trin+b(vrin).

(11)

3 变压器油箱温度场及热点计算

3.1 物理场设置及油箱网格剖分

模拟计算油箱温度场时，只考虑油箱内的传热过程，将绕组、铁心和夹件作为主要热源，金属结构件设为固体传热，变压器油为流体传热；油的流动设置为层流，油箱入口油速(入口处油的法向速度，以下同)取为固定值，出口为开放边界；油箱中间剖面为流体对称面，外表面为热通量边界，对流换热系数对垂直外表面取10，对上表面取8，对下表面取6。

建模时取变压器油箱几何模型的一半，如图4所示。进行网格剖分时，变压器油域的剖分为流体动力学较粗化，流固交界面为流体动力学常规，同时生成两层边界层，绕组最大单元大小为15 mm，其余为普通物理常规剖分。油箱网格单元总数为1 535 700，平均单元质量为0.659 3。

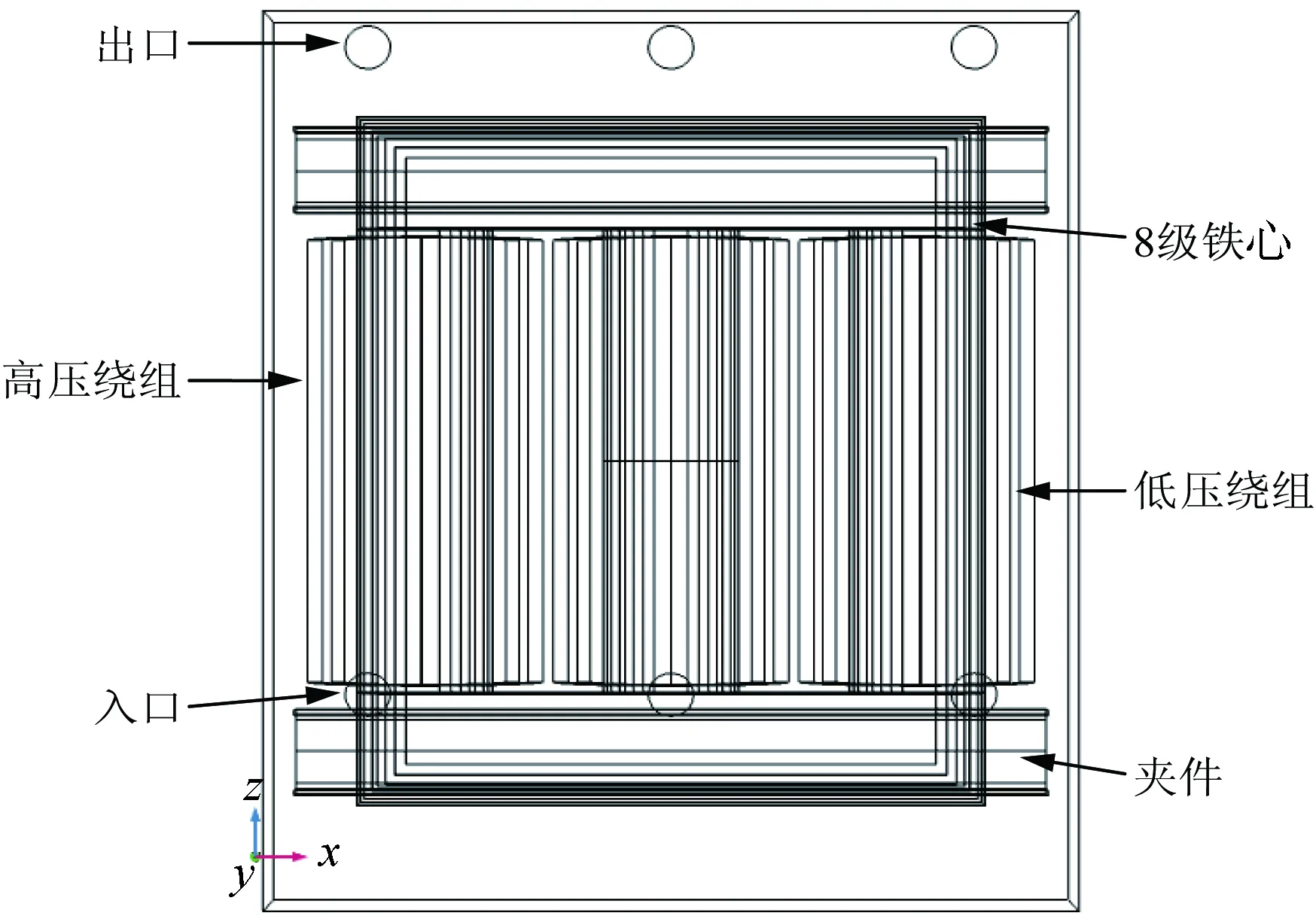
图4 变压器油箱几何模型Fig.4 Geometry model of transformer oil tank

3.2 油箱和散热器出入口油温互约束模型

油箱的模拟计算域中包括3个出口和3个入口，为简化计算，假设油箱3个入口油温和油速相同，油箱出口油温和油速取3个出口油温和油速的平均值。

变压器实际运行时，散热器与油箱相连接，油箱出入口油温、油速和散热器出入口油温、油速之间须满足一定的约束关系，即：油箱入口油温Ttin等于散热器出口油温Trout，散热器入口油温Trin等于油箱出口油温Ttout；油箱入口油速vtin等于散热器出口油速vrout，散热器入口油速vrin等于油箱出口油速vtout。由于建模误差等原因，在变压器温度场模拟计算中完全满足上述约束关系会使得计算很难收敛，本文在计算中取：Ttin=Trout、Trin=Ttout和vrin=vtout，并设置油箱入口油速vtin为固定值，则式(11)可以写成

Ttin=k(vtout)Ttout+b(vtout).

(12)

式中k(vtout)和b(vtout)表示k和b是vtout的函数。式(12)在本质上体现了油箱和散热器出入口油温的相互约束关系，本文称之为“油箱和散热器出入口油温的互约束模型”。

模拟计算时，先进行初始化，设定油箱入口油温和出口油速的初始值Tt0和vtout0，并将油箱入口油速vtin设为固定值。利用Comsol软件进行分离式求解：首先，计算油箱温度场得到出口油温Ttout，然后计算油箱内油的速度场和压力得到油箱出口油速vtout；随后利用式(12)计算油箱入口油温Ttin，再次求解油箱内部热流场得到油箱出口油温Ttout和油速vtout，循环计算直到油箱内部热流场变化满足误差设置要求，计算结束。由式(12)计算Ttin时，注意到vrin=vtout，则k(vtout)和b(vtout)可由式(9)和式(10)求得。在Comsol软件中利用探针变量进行编程即可实现上述方法。

3.3 油箱温度场和热点计算结果及分析

图5为散热器自然对流情况下，油箱入口油速vtin固定为0.05 m/s时，不同负载率的油箱温度场分布。由图5中的速度场的矢量方向可以看出：油箱内存在4个油的涡流区，分布在铁心的4个外顶角处，旋涡方向对角相同，上下及左右相反；当负载率大于0.75后B相入口下方油流在x轴方向的反向；油箱上方出口处的涡流油温较高，热量主要从这里导出；当负载率为0.50时〔如图5(a)〕，由于变压器油的导热系数较小，油与铁心的温差较大；当负载率增大到1.25时〔如图5(d)〕，油箱出口油温升高，油箱入口油温也升高，油与铁心的温差减少。

由图5可知，随着负载率增大，油箱内的温度快速上升，绕组的热耗率开始高于铁心，温度最大值逐渐从铁心转移到绕组上，负载率大于0.75后〔如图5(b)〕，最热点位于低压绕组的上端，且由于中间相冷油注入有利于散热，热点出现在低压绕组A相和C相靠近铁心内框一侧。

图6为强制风冷情况下，油箱入口油速vtin固定为0.05 m/s时，不同负载率的变压器热点分布。由于变压器绕组的温度场呈左右近似对称分布，图6中只给出了B、C两相的热点分布，取热点温度

图5 自然对流时不同负载率下油箱对称面温度分布Fig.5 Temperature distribution on symmetry plane of oil tank at different load rates in natural convection condition

低1 K为温度显示最低值。由图6可以看出：热点位置始终在低压绕组上端，与相关文献[4-5，11]的结论相同，同时，热点在绕组上的高度也随负载率的增加而下移；当负载率为0.50时，热点位于低压绕组高度的100%处〔如图6(a)〕；负载率为0.75时，热点位于绕组高度的98.16%处〔如图6(b)〕；负载率为1.00时，热点位于绕组高度的90.18%处〔如图6(c)〕；负载率1.25时，热点位于绕组高度的80.98%处〔如图6(d)〕。这一结论与相关文献[11-13]一致。由图6可知，热点温度值随负载率的增加快速增大，当负载率为1.25时，热点温度接近临界值98 ℃。

表3为自然对流冷却和强制风冷情况下，不同负载率时油箱入口油温由设定的初始值293.15 K(20 ℃)经迭代计算后得到的稳态值，可以看出，随着负载率的增加，油箱入口油温也快速升高。而对于相同的负载率，强制风冷时油箱入口的油温要小于自然对流冷却时油箱入口的油温，且负载率越大，差距越明显。

使用分体解耦方法对变压器的温度场进行模拟计算时无须考虑多个散热器组的剖分，只针对多个散热器组中的1个进行网格细分，避免了大量重复性网格划分和计算工作；将散热器组和油箱分开建模和计算，解决了变压器整体剖分时单元尺寸差异较大导致的计算精度和收敛性差的问题，计算量和迭代次数明显减少。前述算例中，分离式求解器循环次数最多为45次，最少为32次(相对容差0.000 1、油箱入口油温初始值293.15 K)，与文献[11]的循环次数(达到104次)相比，计算量和迭代次数显著减少。

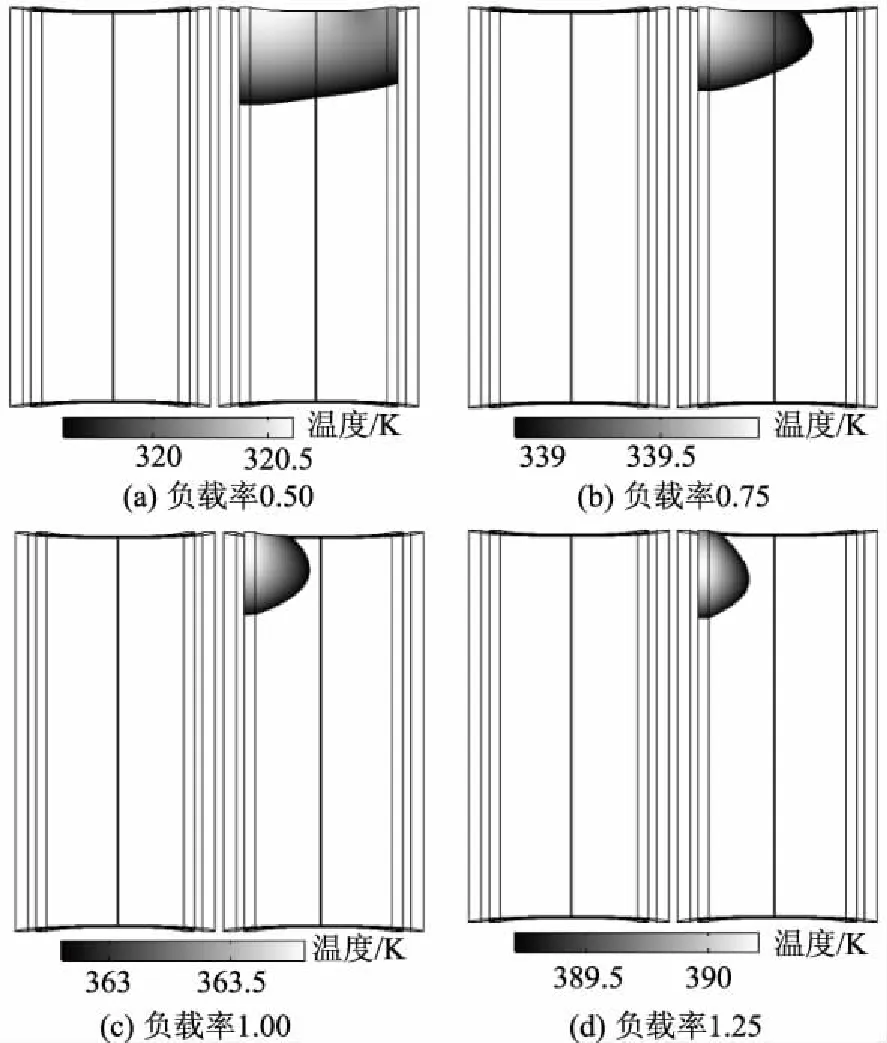
图6 强制风冷时不同负载率下的热点分布Fig.6 Hotspot distribution at different load rates in forced air-cooling condition

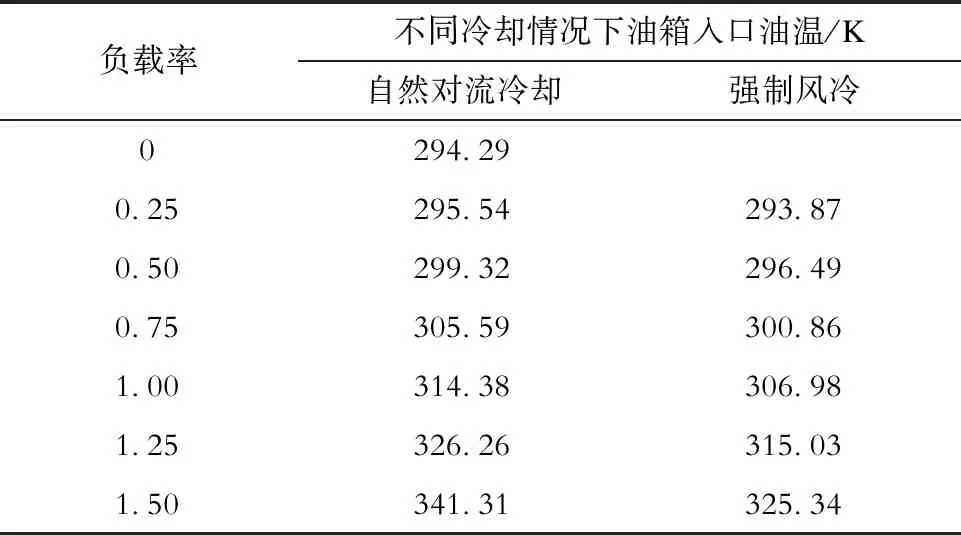
表3 不同负载率时油箱入口油温稳态值Tab.3 Steady-state values of inlet oil temperatures of oil tank at different load rates

为验证本文计算方法的准确性，与采用文献[23](负载导则)给出的计算公式在散热器自然对流情况下，对S9-1600/10/0.4型变压器在不同负载率时的热点值进行比较，结果见表4，可以看出，本文的模拟计算值与导则计算值较为接近。

表4 本文热点计算值和负载导则计算值对比 Tab.4 Comparisons of hotspot calculation results by the method in this paper and by loading guide

4 结论

本文针对变压器温度场模拟中整体模型计算复杂度和简化模型误差水平之间的矛盾，提出一种分体解耦的计算方法，并利用油箱和散热器出入口油温互约束模型对不同工况下的变压器温度场进行模拟，得出以下结论：

a)算例模拟结果表明，采用基于油箱和散热器出入口油温互约束模型的分体解耦计算方法时，变压器在不同负载率下的温度场、热点值等均符合相关理论分析结果，且具有较高的准确性；同时提高了计算效率，减少了计算量和计算迭代次数。

b)分体解耦方法允许不同组件采用不同的数值方法或热路法，对可以简化计算的组件采用简单的算法，对需要精确分析的组件可以采用精度更高的算法或较细的网格，从而实现优化计算资源分配的目的。