孤岛微电网的分布式有限时间事件触发二次协调控制

周建萍，张 健，茅大钧，葛祥一，叶剑桥，方 乐

（上海电力大学 自动化工程学院，上海 200090）

0 引言

近年来，随着分布式电源（DG）的广泛应用，集成大量DG 的微电网系统得以迅速发展。微电网是可运行在并网模式或者孤岛模式下［1］，具有DG、能量储存和本地负载的低压网络。并网模式下，微电网电压和角频率参考值可由主网提供，通过联络线实现与主网的功率交换。孤岛模式下，微电网将面临更严峻的问题，既要求微电网系统自行维持角频率和电压的稳定以及实现有功和无功分配，又必须随时保持供需平衡，否则会导致系统稳态角频率和电压偏移额定值。因此，合理的角频率和电压控制策略是实现其自身稳定运行的关键。为了补偿传统下垂控制导致孤岛微电网系统的稳态角频率和电压偏差，提出了二次协调控制［1］。

孤岛微电网二次协调控制是通过电压和角频率的给定参考值计算得到相应的调整量，反馈给初次控制并进行补偿。二次协调控制分为集中式控制结构和分布式控制结构。集中式控制结构是利用中央处理器检测系统的电压和角频率，使用比例积分控制器为初次控制设置参考值，而分布式控制结构则不需要建立中央控制器来收集所有本地控制器的信息，只需要和相邻控制器之间交换信息即可，并且可以进行并行数据处理以提高响应速度。因此文献［2-3］将分布式多智能体系统MAS（Multi Agent System）结构用于孤岛微电网的二次协调控制中，将孤岛微电网二次协调控制问题转化为MAS 追踪同步问题，即视微电网中的DG为MAS中的智能体，同时将电压和角频率期望值设置为虚拟领航者，只需小部分DG直接访问领航者，电压和角频率可以通过相邻DG之间的通信来准确恢复到参考值。文献［2］和文献［3］分别提出了分布式固定时间控制方法和分布式均值法来实现电压和角频率的二次协调控制。进一步地，文献［3］利用内模设计方法，保证了功率按下垂系数分配。文献［4］则是从离散化角度来设计角频率、电压二次协调控制。

大多数二次协调控制策略只能达到渐近一致性，这意味着收敛速度至多呈指数型增加。但是，在某些工程应用中，要求在有限时间内收敛才能达成一致性（例如当控制精度至关重要时）。因此，研究微电网有限时间下的二次协调控制具有十分重大的实际意义。文献［5］在有限时间内实现了电压和角频率恢复控制以及准确的有功功率分配。文献［6］提出了一种鲁棒的有限时间控制算法对孤岛微电网进行二次协调控制，对于各种干扰和参数扰动下，其收敛性可以得到保持。文献［7］和文献［8］分别提出了具有无界控制输入和有界控制输入的有限时间二次协调控制策略。相比文献［7］，文献［8］采用饱和功能避免超出控制输入范围以实现有界控制输入的有限时间二次协调控制，通过这种控制算法，可以在有限时间内实现系统角频率恢复至额定角频率以及精确的有功功率分配，并抑制了瞬态过冲。

上述方法均是基于周期性采样控制策略，这意味着各DG 之间的通信负担大，然而在实践中，通信带宽往往是有限的。因此，为了减轻通信负担，提出了基于事件触发控制机制的孤岛微电网二次协调控制［9］。事件触发控制机制是指控制任务按需执行，在保证控制性能的前提下，减少通信主体之间的通信次数，避免了大量的冗余信息传输。事件触发控制不仅需要设计事件触发函数，还需证明其具有正的最小事件间隔时间（排除Zeno 现象）。文献［10］采用分布式事件触发控制策略用于孤岛微电网二次电压控制。进一步地，文献［11］将分布式事件触发控制策略用于电压和角频率的二次协调控制以及实现准确的有功功率比例分配，由于对于电压-无功平衡中的无功功率采用的是滤波前后的差值，这使得电压的控制更加准确。文献［12］将事件触发控制应用于多混合储能的孤岛微电网的分层协调控制中。

基于上述研究成果，为了加快孤岛微电网二次协调控制在事件触发下的响应速度，增强系统抗干扰能力以及提升系统的即插即用性能，设计了一种基于有限时间下的分布式事件触发控制算法。该算法是以一致性收敛速度为突破口，通过设计有限的时间上限来提高收敛速度。同时所提策略既能使微电网实现电压、角频率二次协调控制以及功率均分控制，又解决了传统二次协调控制中连续通信导致通信耗能大的问题。李雅普诺夫稳定理论和仿真实例验证了所提策略的可行性和有效性。

1 孤岛微电网的分布式控制结构和图论

1.1 孤岛微电网的分布式控制结构

图1 为孤岛微电网基于电压源变换器（VSC）的分布式控制结构图，由能量源、VSC、串联LC 滤波器、RL 输出连接器和局部控制器组成，其中，局部控制器包含功率、电压和电流控制回路。图中，p′、q′分别为线性化前有功功率和无功功率；P、Q分别为线性化后有功功率和无功功率；ix（x=a，b，c）为三相电流；igx为滤波后三相电流；Vdc为直流源的直流电压；md、mq分别为电压、电流控制环输出调制比的d轴和q轴分量；Vdref、Vqref分别为输入电压d轴、q轴分量的参考值；ω为输出角频率；ω0为二次控制角频率输出值；v0为二次控制电压输出值；DP、DQ分别为有功功率下垂系数和无功功率下垂系数。

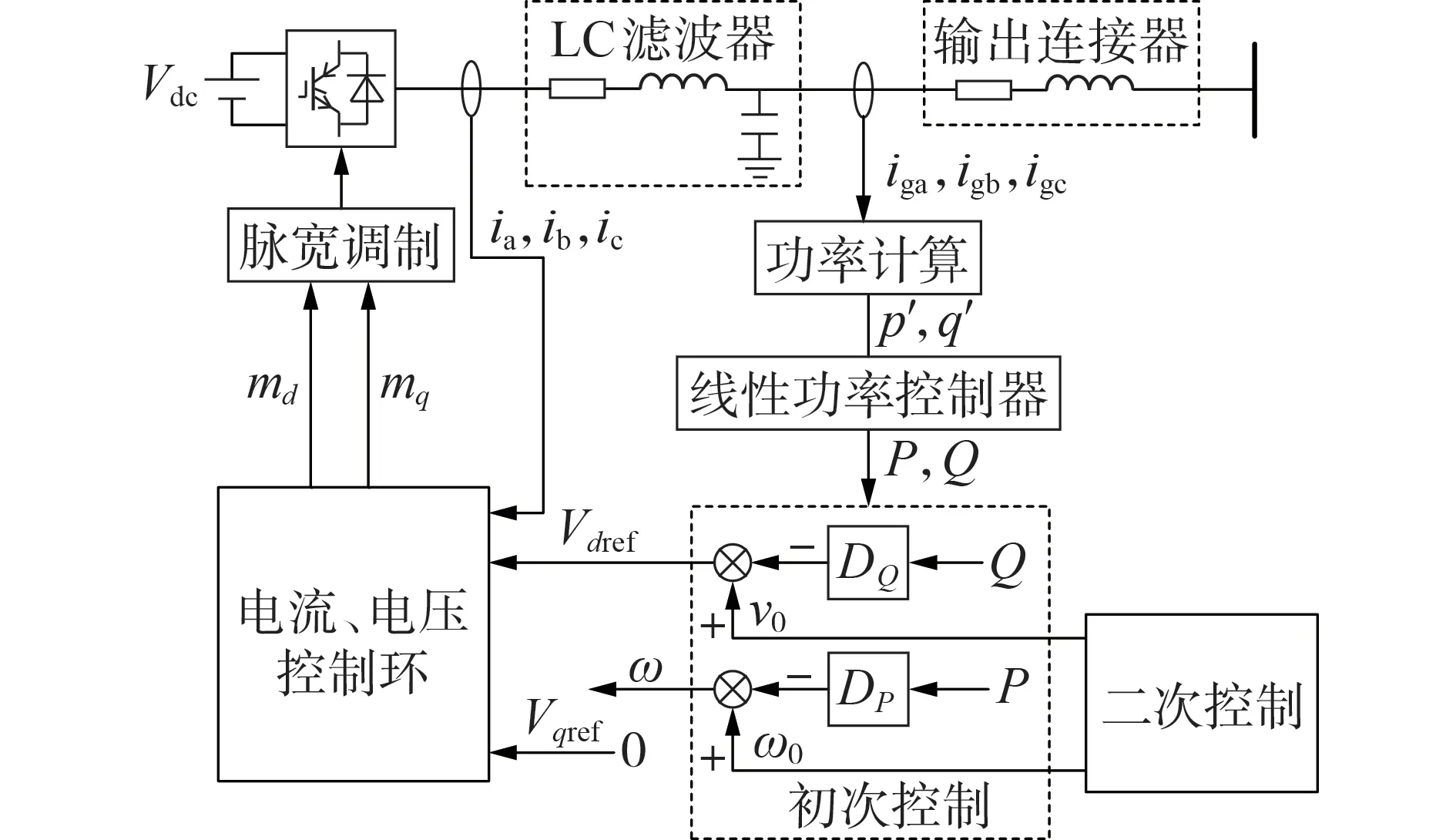
图1 孤岛微电网分布式控制结构Fig.1 Distributed control structure of islanded microgrid

下垂控制广泛应用于孤岛微电网初次控制，初次控制通常可利用P-ω和Q-V下垂控制实现［13］，分别如式（1）、（2）所示。

式中：ωi、vi分别为DGi的输出角频率和电压幅值；ωni、vni分别为DGi的ωi、vi的参考值，由二次协调控制给定；Pi、Qi分别为DGi的有功功率、无功功率输出值；DPi、DQi分别为DGi的有功功率下垂系数、无功功率下垂系数。通常，可以分别通过式（3）、（4）所示的一阶低通滤波器来获得Pi和Qi［14］，其中p′i和q′i由式（5）、（6）所示的功率计算模块计算得出［15］。

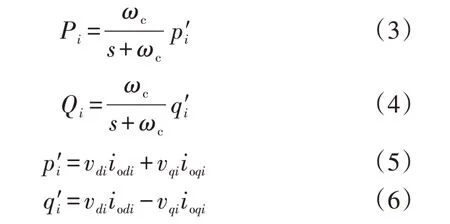
式中：ωc为低通滤波器截止角频率，取31.25 rad／s；vdi、vqi分别为vi的d轴、q轴分量；iodi、ioqi分别为ix的d轴、q轴分量。下垂控制器在dq坐标系下进行设计，电压参考值基于d轴定向，即vdi=vi和vqi=0。

为了补偿下垂控制所导致的角频率和电压偏离额定值，本文采用分布式有限时间事件触发二次协调控制来设计新的参考值ωni和vni，使得DGi输出ωi和vi恢复至所设计的额定值以补偿偏差。

1.2 图论

2 有限时间事件触发二次协调控制设计

在大多数二次协调控制的收敛方法中，收敛时间都是未知的，并且是在无限时间范围内实现DG系统的一致性收敛。在本节中，设计有限时间事件触发二次协调控制算法，以消除角频率和电压偏差以及实现精准的有功功率比例分配，同时根据李雅普诺夫函数从给定初始衰减到0 的时间来估算收敛时间，以及给出事件触发函数来确定事件触发时刻。有限时间事件触发二次协调控制算法中，收敛时间大幅缩短，这在快速操作中是理想的，结合事件触发机制则可以减少DG 之间的通信次数以达到节约硬件资源的目的。有限时间事件触发二次协调控制具有如下的期望。

1）角频率二次协调控制及有功功率分配。存在角频率恢复时间Tf、有功功率恢复时间TP使各个DG下垂控制的ωni都满足式（7）、（8）所示关系式。

式（7）—（10）表示所设计策略使系统在对应的有限时间实现恢复控制，式（11）表示避免所设计事件触发策略在某段时间内发生无限次事件触发。

2.1 角频率二次协调控制及有功功率分配设计

角频率二次协调控制及有功功率分配的目的是设计初次控制输出角频率参考值ωni，使各个DG 的输出角频率ωi恢复到额定值。通过使用输入输出反馈线性化方法，对式（1）求导获得ωni的动态系统为：

式中：αωi、αPi分别为DGi的角频率控制增益和有功功率控制增益，αωi，αPi∈（0，1）；βωi、βPi分别为DGi的角频率放大系数和有功功率放大系数，且βωi，βPi>0；bi为领导者连接系数，若DGi与虚拟领导者相连，则bi=1，否则bi=0；sig｛·｝=sign（·）| |· ，sign（·）为符号函数。

为了降低DG 之间对通信网络的依赖程度，将角频率和有功功率状态估计值代替式（14）中的实际值。则uωi和uPi可进一步改写为：

式中：上标“^”表示相应变量的估计值；lωi、lPi分别表示DGi的角频率控制器、有功功率控制器发生第l次事件触发。定义角频率测量误差eωi(t)和有功功率测量误差ePi（t）分别为：

图2 事件触发机制Fig.2 Event-tiggered generation mechanism

针对角频率二次协调控制与有功功率分配的分布式有限时间事件触发函数设计和证明如下。

结合式（16）和式（17），则式（15）可写成：

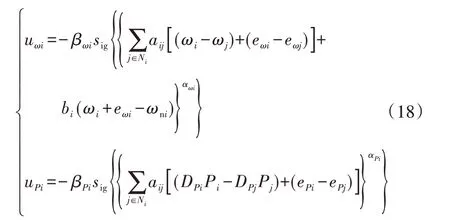
定义角频率误差εωi(t)=ωi(t)-ωni，则式（18）可写成：

考虑DG 间的无向通信拓扑是连通的，且至少1个DG 能够获取参考角频率信息，则在辅助控制器式（15）的作用下，采用如式（13）所示的一次角频率控制参考值，使系统能在有限时间内实现角频率二次协调控制和有功功率的比例分配。本文设计了如式（22）所示事件触发函数。

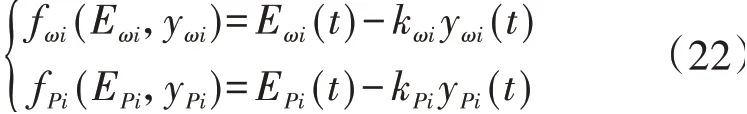
式中：以角频率事件触发为例，非负序数kωi规定了Eωi/yωi的上界，将Eωi/yωi=kωi作为事件触发时刻，DGi传输信息，初始化角频率状态估计器输出为实际角频率值ωi(tlωi)，同时Eωi/yωi复归0。而当Eωi/yωi0，kPi>0，详细推导及李雅普诺夫稳定性证明见附录A［16］。

式中：λmax(L+D)表示矩阵L+D的最大特征值；ki为任意DGi所对应的kωi、kPi或者kVi。

经过上述分析，角频率二次协调控制和有功功率比例分配的分布式有限时间事件触发二次协调控制设计见附录C图C1。

2.2 电压二次协调控制设计

电压二次协调控制的目的是设计初次控制输出电压参考值vni，使各个DG的输出电压幅值恢复到额定值。对式（2）求导以获得vni的动态系统为：

式中：非负系数kvi>0。

电压二次协调控制的分布式有限时间事件触发二次协调控制见附录C 图C2。分布式有限时间事件触发二次协调控制框架见附录C图C3。

3 仿真算法分析

为验证本文提出的孤岛微电网的分布式有限时间事件触发二次协调控制策略的有效性，在MATLAB／Simulink 中搭建包含4 个DG、额定输出电压幅值为380 V 且额定角频率为50 Hz 的孤岛微电网模型，如附录C 图C4 所示，相关参数见附录C表C1—C3。

为测试所提策略的动态响应特性，仿真过程分成2个阶段：［0，3）s采用初次控制，即仅采用下垂控制；第3 s加入所设计的分布式有限时间事件触发二次协调控制。

3.1 所提策略的响应实验

分布式有限时间事件触发二次协调控制的输出波形见附录D图D1—D4。由图可知：在3 s之前，仅靠下垂控制可使系统的角频率达到稳定，但不能稳定在100π rad／s，输出电压达到稳定，但无法稳定在380 V，所以下垂控制会使系统产生稳态偏移；在3 s 时，加入二次协调控制后，使得系统角频率逐渐稳定至额定值，输出电压也稳定至额定值。可以看出，DG 输出的有功功率反比于下垂系数，实现了有功功率比例分配。这说明所提策略能有效实现无静差控制，同时实现有功功率比例分配。

针对所提策略的事件触发时刻，以3～4 s为例（其中具体事件触发次数见附录D 表D1，平均通信时间间隔见附录D表D2，可知有限时间事件触发控制，角频率、电压和有功功率在分布式事件触发控制的离散通信行为下可实现信息交换，因此减少了信息交换量，同时降低了对通信网络的要求。

3.2 所提策略与传统策略对比实验

图3为采用3种不同策略下角频率、电压幅值对比图。本文分别选择DG3的角频率和DG1的电压进行对比。由图可知，所提出的分布式有限时间事件触发二次协调控制取得了最快的收敛速度。

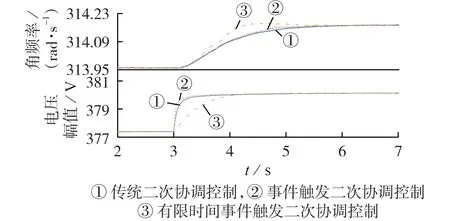
图3 3种不同策略的实验结果对比Fig.3 Comparison of experimental results among three different strategies

3.3 负荷切换测试实验

所提策略在7 s 时负荷切换的波形响应图见附录E 图E1。由图可知，负荷切换电压幅值、角频率、有功功率和有功功率分配在经过小的波动后稳定在所期望的稳态，说明在所提策略下，系统切换负荷后，经过小波动能保持稳定。

3.4 即插即用测试实验

本节测试所提策略的即插即用能力。在7 s 时断开DG4与系统的连接，并在9 s 时重新连接。由附录C 图C4 可知，当断开DG4时，DG1—DG3与期望值仍能组成一个完整系统，依旧可以从虚拟领导节点接收信息。因此，DG1—DG3仍可以实现二次协调控制的目的。实验结果如图4 所示，当重新连接DG4时，系统将承受严重的振荡，这是因为未实现预同步。但是，系统角频率波动范围保持在［311，316］rad／s，说明即使在这种情况下，系统仍然可以保持稳定。

4 结论

为了解决传统下垂控制电压和角频率偏移以及通信负担大等问题，本文基于DG 自身信息和其相邻DG 信息，设计了分布式有限时间事件触发二次协调控制。所设计方案在有限时间内解决角频率和电压偏移问题，且实现了有功功率比例分配，在提高收敛速度的同时，利用李雅普诺夫稳定理论设计事件触发函数以减少系统的通信次数，节约通信资源。基于仿真实验结果可得如下结论。

1）所提策略能补偿传统下垂控制引起的角频率和电压偏移，使角频率和电压恢复至额定值，且实现有功功率比例分配，保证孤岛微电网的稳定运行。

2）所设计的分布式有限时间事件触发控制机制，能在保证系统稳态性能的前提下，减少系统的通信次数，节约通信资源。负荷切换时，能快速协调控制角频率和电压达到期望值，具有即插即用的功能。

3）采用分布式有限时间事件触发二次协调控制能够更有效地加快微电网的角频率和电压的响应特性，提高收敛速度。

附录见本刊网络版（http：//www.epae.cn）。