趣味数学：“数与形”教学的应然追求

梁求玉 郑祥旦

摘要：“数与形”源自趣味数学，“数与形”一课可上成趣味数学课。其教学流程可以是先明确“数”与“形”的概念，再用不同的“单子”把平方数排列成正方形图案，让学生反思图案之间的关系并把平方数用加法算式表达出来，最后仿照排列“四角数”的方法排列出“三角数”“五角数”“六角数”。在这样的课堂中，学生像毕达哥拉斯及其弟子一样安安心心地“玩了一把”，从中感悟到了数学的奇妙，体会到了学习数学的乐趣，进而对数学充满了好奇心。

关键词：“数与形”;趣味数学;教学原本;玩中学

人教版《义务教育教科书·数学》六年级上册“数学广角”中的例1“数与形”源自于毕达哥拉斯学派对趣味数学的贡献。据说，毕达哥拉斯及其弟子非常重视数与图形之间的关系，他们用一种名叫“单子”的符号●排列成优美的图形来表达一个数。用“单子”排列成三角图形的数叫做“三角数”，排列成正方形的数叫做“四角数”。也许就是他们对数字的崇拜，促使他们在数字的探索中发现了大量的奥妙，其中许多是对后来影响很大的趣味数学问题。

如果把“数与形”这一课上成趣味数学课，还原知识产生的本原，让学生安安心心地“玩一把”，在玩中深刻地体会到“数”与“形”之间的“两依倚”，那么学生在解决问题时就不会出现或少出现“两边飞”的情形。为了使教学的进程是可视的，本课的教学目标可以定位为：学生用“单子”把平方数排列成正方形图案，反思图案之间的关系把“四角数”用加法算式表达出来;仿照“四角数”，排列出“三角数”“五角数”“六角数”;感悟数学的奇妙，体会学习数学的乐趣，对数学充满好奇心。

应该如何上这节课呢？有很多教师把教学目标定位为“发现图形中隐藏着数的规律”，或者以形助数，或者以数解形，或者数形结合，一节课在寻找规律、发现规律、运用规律，从思维的角度上说，这与一年级“找规律”教学没有太多的区别，只注重知识的教与学，就没上出“趣味数学”的味道。

毕达哥拉斯学派信奉“万物皆数”，他们认为，“一切事物都按数来安排”，他们最先把自然数分成奇数和偶数，研究发现了完全数、友数、毕达哥拉斯数，等等。因此，学生首先要明确“数”是指整数，是一列整数。

形数原意为“石子”，毕达哥拉斯和他的学生们很可能是在沙滩上用石子作为“单子”摆出优美的图形。如果有学生把“单子”理解为正方形，那就错了。“单子”除了是正方形外，还可以石子、圆形、三角形、星形、点子，等等。

假设学生已经阅读了本课的教材内容，不同的学生对“四角数”及相关的习题有不同的理解掌握，那么，教学的导入环节可以这样设计。

出示课题“数与形”。引导学生用说词解字、互动交流的方式说一说“数”和“形”的意思：“形”是用正方形、小石子、星形等物体摆出来的图形;“数”是一个或一列整数。

“百数表”是整数数列的初始部分，在数学研究、数学教学中都占有十分重要的地位，可以这样说，如果学生学会了“百数表”中的相关知识，那么他们学习这部分知识就不会有太大的困难，至少不会成为潜能生。因此，教学的动手操作互环节可以从“百数表”入手，教学可以如下设计。

教师出示“百数表”，提醒学生“数”就藏在这个“百数表”里。让学生先数数：1，2，3，…;写出每一整数的平方并计算它们的值：1=1，2=4.3=9……

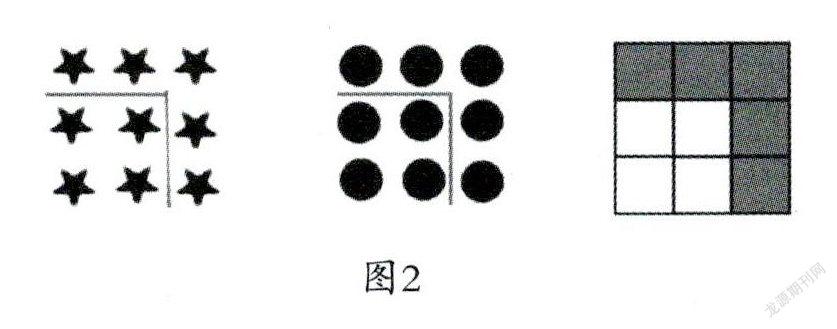
引导学生独立思考，并各自用不同的“单子”把1、3、9等平方数依次排列出优美的图案，动手操作后在小组内组织学生之间的互相观察并欣赏自己的作品，教师选择部分作品投影出来供全班学生点评。学生创造出来的图案可能如图1。

教師要引导学生找出图案的共性，即从整体上看这些图案都有正方形的外形。可以向学生介绍“形数”产生的历史：最先排列出这些图案的人是古希腊的毕达哥拉斯和他的学生，他们还把这些平方数叫做“四角数”。由于语言的不同，有的外国人把正方形叫做四角形，所以“四角数”其实就是“正方形数”。

首先，教师提示学生在这些图形里蕴藏着许多数学的奥秘，现在需要他们通过自己的眼睛和大脑把这些奥秘给挖掘出来。可以引导学生先观察自己摆出的第3个图，用反向思考的方法回顾前面的动手操作过程，画图表示出它与前一幅图之间所具有的包含与被包含逻辑关系做口图2）。

再次，引导学生观察算式：4+5=9，1+3=4，得到：1+3+5=9。推想并验证：1+3+5+7=16，4×2-1=7，其图形是n=4的正方形;1+3+5+7+9=25，5×2-1=9，其图形是n=5的正方形。运用规律解决问题：1+3+5+7+…+（）=100，其图形是n=10的正方形。

然后，引导学生在“百数表”中观察每个算式的数，得到：1+3+5=32，1+3=22。推理得出：1=1。学生主动改写其余的算式。再观察得到：每个算式的加法是连续的奇数，概括其数学发现：从1起，n个奇数的和等于n;算式的最后一个加数是2n-1。有学生还可能表示他对n2和2n的联系与区别有新的理解。

最后，引导学生反思：学习本课之前，你发现了奇数与平方数之间奇妙的关系了吗？学习时你是用什么方法发现的？回顾上述的学习过程：先把平方数转化图形，再把图形转化为奇数的和。通过教师适时地概括：在数学上，把这种方法叫做“数形结合”，学生就能够在头脑中牢固地建立“数形结合”的印象。

学习活动的本质是“自由”，学习的发展是有层次的，即自己学、自觉学、自主学。学生的自主学习从某个角度上来说是一个“美丽的谎言”，因为严格意义上的自主学习是成人的事。Holec认为，自主学习是“能够就学习过程中所遇到的各种问题进行决策的能力，包括确定学习目标、内容和进度，选择学习方法和技巧，监控严格意义上的语言习得过程（包括学习的节奏、时间、地点等），评估已掌握的知识”。因此，教育意义上的自主学习是可能存在的。课堂上，首先必须扎实做好“自己学”和“自觉学”。在上述的教学活动中，在教师的指导下，学生进行了很大程度上的“自己学”，接下来，要引导学生进行“自觉学”，可以如下教学设计。

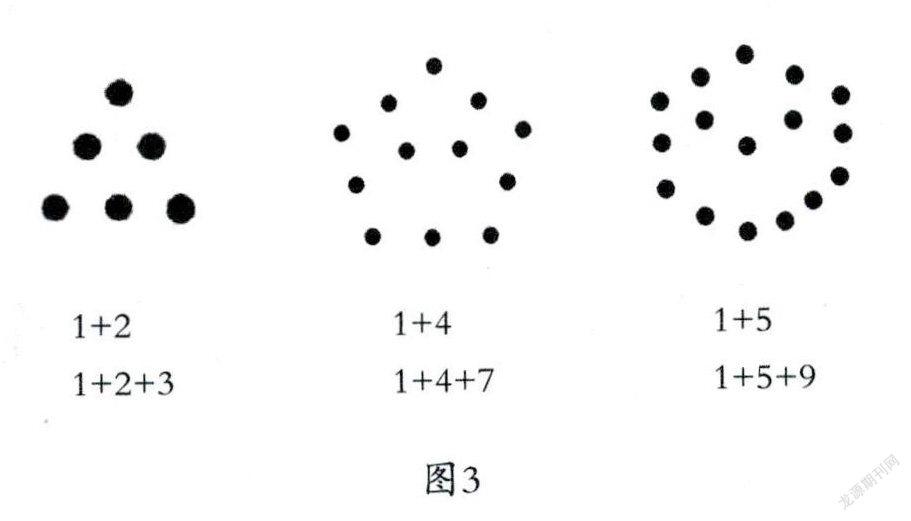
首先，要引导学生质疑，学生可能说：“用‘单子’排列了“四角数”，还能排列‘三角数“五角数“六角数’吗？”教师鼓励学生用“单子”排列一个三角形、五角形、六角形，再把边进行扩大，用算式表示图形。（如图3）如果学生没有这种质疑能力，也可用师生互动的方式进行教学。

說明：这些算式只是例子，以写5个加数为宜，可不要求进行求和计算。

此外，可以引导学生对是否存在“七角数”“八角数”进行猜想;也可以把这些“三角数”“四角数”“五角数”“六角数”写成数列，引导学生根据“百数表”写出别的数列;总之，可以把有限的学习引向无限的探索。

综上所述，自主学习是通过“自己学、自觉学、自主学”有层次地发展起来的，在本课中学生先“自己学”“四角数”，动手玩，用“单子”排列平方数把“数”转化为“形”，“解剖”图形把“形”转化为“数”，归纳出平方数与奇数的关系，感悟图形在转化过程所起的作用：形成元认知—数形结合。接着，运用数形结合的方法自觉学“三角数”“五角数”“六角数”形成了“形数”的知识体系。

进一步来讲，趣味数学是别样的数学，它集知识性与趣味性为一体，用权威的数学理念与独特的思维方式引导学生学数学。趣味数学课是让学生感受别样的数学，重在引导学生自我探索、自主表达、激发兴趣、持续创新等，目的是真正培养学生的多元思维和解决问题的能力，让学生走近数学、爱上数学，在趣味中学习，在快乐中进步。