拓展思维空间 彰显课堂活力

朱雪平

[摘  要] 数学是一门发展思维能力的学科，数学教学是拓展学生思维空间的教学. 笔者结合教学实际，在思維训练拓展课程与活力课堂的碰撞中发现，可以通过巧置悬念、激发触动、纵横联想、另辟蹊径四个方面有效地组织学生进行思维活动，拓宽学生的思维空间，彰显课堂活力.

[关键词] 拓展课程;思维训练;活力课堂

开展数学拓展性课程，是对现有初中数学教材的有力补充，能丰富教学内容，丰富校园文化建设，促进学校发展. 而对于很多农村学校的初中生来说，由于基础比较薄弱，所以学习数学是一件相当困难的挑战. 数学教学的核心是进行思维训练，由于课堂时间有限，导致课堂中很多的生成资源得不到有效利用，学生的思维受到限制. 那如何在新课改的理念下把思维训练拓展课程与活力课堂有效地结合起来呢？笔者以为可以从以下几个方面着手.

巧置悬念，启迪思维

在数学课堂教学过程中，教师要精心设计一系列问题，产生悬念，从而有效地激发学生的好奇心，引导并鼓励学生提出质疑，因为提出问题比解决问题更重要. 有疑问才会有思考，才会深入探究，才会触动思维，然后在教师的智慧点拨下，释疑解惑. 在这个过程中，学生可能一开始感到有些费力，而后就会感到柳暗花明又一村，这才是我们所追求的富有灵动性的活力课堂.

如教学人教版九年级上册“二次函数专题复习课”时，笔者设计了一节以数形结合思想为主线的复习课. 由于数形结合思想在解决函数的问题上应用非常普遍，所以笔者就这一问题专门在拓展课上进行深入探讨，以下是教学片段.

拓展习题：在实数范围内，方程x2+4=的解有几个？这道题的本质不是考查我们解方程，而是用数形结合思想解决. 于是需要我们抓住本题的本质，悟出出题者的本意，即在平面直角坐标系中分别作出函数y=x2+4和y=的图像，这两个图像的交点个数即为原方程的实数根个数.

这道题充分体现了“数缺形时少直观，形少数时难入微”这句话的真谛. 如果直观地看，学生容易发现这个方程可以化为一个一元三次方程. 在初中阶段，学生还没有学过怎样解一元三次方程，这会使学生产生疑问. 在这种心理状态下，学生开始讨论解决疑问的方法，此时的课堂充满了思维的张力，能让原本“难产”的疑问随着好奇心自然流淌，灵动生长.

激发兴趣，触动思维

课堂中能否调动学生学习的积极性、激发学生的学习兴趣、触动学生的思维是关键. 只有学生对数学学习产生浓厚的兴趣，才会积极地思考，才会快乐地学习，才会提升学生的学力，才会提高学生探索数学世界的主观能动性. 那么在数学教学过程中，如何激发学生的学习兴趣呢？笔者以为可以通过引用故事的方式来激发学生的兴趣.

如教学“函数的概念”时，由于课堂时间比较紧迫，所以教师往往注重知识的传授，而忽视了数学史. 既然拓展课程是课堂教育的延伸，于是笔者把函数概念的历史教学放到拓展课上来进行.

教学中，教师可以列举一些实际问题，得出函数的概念：

一般地，在一个变化过程中，如果有两个变量x，y，并且对于x的每一个确定的值，y都有唯一确定的值与它对应，那么我们就说x是自变量，y是x的函数.

像s=60t，y=50x-0.1这样，用关于自变量的数学式子表示函数与自变量之间的关系，是描述函数的常用方法. 这种式子叫函数解析式.

17世纪，数学家将一个变量x的不同次幂称为x的函数.

1718年，约翰·伯努利首次明确提出函数的新定义：一个变量与一些常数的和、积、商、幂、方根的代数式，称为这个变量的函数.

1748年，欧拉首次用“解析式”定义函数：一个变量的函数是由该变量和一些常量组成的解析式.

在数学课堂教学过程中，结合故事来激发学生的学习兴趣、触动学生的思维，是一种有效的方法. 这种引用历史故事的方式代替了讲授法，能让学生穿越时空，与历史上的数学家“对话”，从而拉近他们与数学之间的距离，让原本难以“下咽”的函数概念灵动，定格在学生的脑海中，镶嵌在学生的思维里，从而更好地培养学生的数学素养.

纵横联想，拓宽思路

在数学教学中，培养学生的思维能力关键在于教给学生思维方法. 教师应善于选择典型例题，善于发现问题的本质，鼓励学生运用多种方法解决问题，这样既有利于培养学生的发散思维能力，又能激发学生的学习兴趣. 教师要善于采用变式题进行教学，这样既能开阔学生的视野，又能让学生的数学思维有生长点和发展点，从而培养学生的数学思维能力.

如教学“圆和相似三角形的复习课”时，由于课堂时间有限，所以学生的多种思路没有办法在课堂上一一呈现，于是笔者就这一问题专门上了一节拓展课，解题成果如下.

如图1，已知A，P，B，C是☉O上的四点，∠APC=∠BPC=60°，AB与PC交于点Q.

（1）判断△ABC的形状，并证明你的结论;

（2）直接写出所有与△APQ相似的三角形;

（3）若AP=6，=，求PB的长.

对于第（1）问，只要运用圆周角的性质，学生很快就能解决;第（2）问也相对比较简单，而第（3）问有很多解决方法，具体呈现如下.

设AQ=3x，则BQ=5x，BC=AB=8x.

方法一，因为△APQ ∽△CBQ，所以=，解得PQ=. 又△APQ ∽△CPB，所以=，解得PB=10.

方法二，因为△APQ∽△CPB，所以=，解得PC=16. 又△BCQ ∽△PCB，所以=，解得PB=10.

方法三，因为△APQ ∽△CBQ，所以=，解得CQ=4x2. 又△PBQ ∽△ACQ，所以=，解得PB=10.

方法四，如图2，过点A作AM⊥PC于点M，过点B作BN⊥PC于点N. 因为△AMQ∽△BNQ，所以==. 又△APM ∽△BPN，所以==. 所以PB=10.

方法五，因为△AMQ ∽△BNQ，所以 ==. 容易求得AM=APsin60°，BN=BPsin60°，所以=. 所以PB=10.

方法六，如圖3，运用面积方法建立比例求解. 过点Q分别作QE⊥PA于点E，QF⊥PB于点F. 因为∠APC=∠BPC=60°，所以QE=QF. 所以===，即=，解得PB=10.

在数学教学过程中，变式教学和一题多解显得尤为重要. 教学中，我们应让学生在变式中抓住问题的本质，洞察问题的结构，追求“做一题，会一类，通一片”. 一题多解属于发散性思维的范畴，如果教师善于选题，善于启发，善于捕捉学生思维的“星星之火”，那么课堂的气氛就会引发为“燎原之势”，这样就会使课堂教学产生一种吸引人的魅力.

另辟蹊径，激活思维

在数学课堂教学中，学生常常会陷入一种思维怪圈，也就是我们经常所说的思维定式，即在头脑中用一种固定的思维模式去思考问题. 每当呈现给学生的问题跟他们的已有认知水平发生冲突时，学生就会感到束手无策. 在这一关键时刻，教师应启示一条全新的思维路子，使学生燃起新的希望，让希望在数学课堂上落地生根，在数学的天地里播撒思维种子.

在初中阶段，几何学习是一个基础，一道好的几何试题可以涉及很多的知识点，包括三角形、四边形、圆，甚至包括考查知识迁移能力和知识整合能力. 对于学生来说，几何是一种对思维深度和梯度的考验，而且几何题往往解题思路比较多，所以能充分激活学生的思维. 下面是一节拓展课的教学片段.

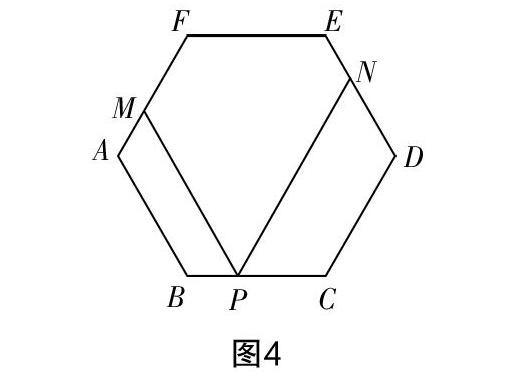
如图4，正六边形ABCDEF的边长为a，P是BC边上一动点，过点P作PM∥AB交AF于点M，作PN∥CD交DE于点N.

（1）∠MPN=______;

（2）求证：PM+PN=3a.

此题的第（1）问比较简单，学生自己便可以解决. 第（2）问的证法比较多，在拓展课上，笔者展示了常规思维的证法和巧妙独到的证法. 第（2）问的普遍证法如下：

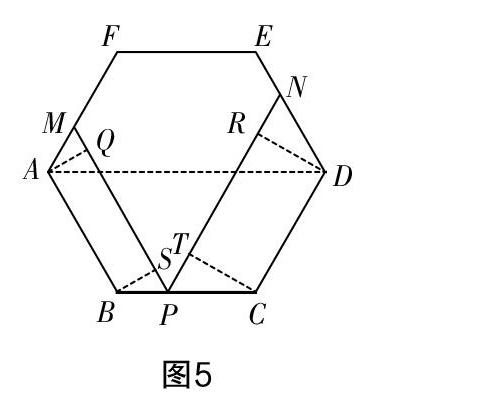
如图5，分别过A，B两点作PM的垂线，垂足分别为Q，S，分别过C，D两点作PN的垂线，垂足分别为T，R. 因为∠BPS=∠CPT=60°，所以SP=BP，PT=CP. 所以SP+PT=. 又四边形ABPM和四边形CDNP都是等腰梯形，所以MQ=PS，NR=PT，QS=AB，RT=CD. 所以PM+PN=3a.

教师引导学生走另外一种思路：能不能在六边形的外面作辅助线来解决？学生通过思考和合作交流，马上想到了形外连线的方法.

新颖的证法：（形外连线）如图6，延长FA，CB交于点I，延长BC，ED交于点J，则△ABI，△DCJ，△PMI，△PNJ均为等边三角形. 所以PM+PN=PI+PJ=BI+BC+CJ=3a.

“拓展课程”是“基础课程”的补充，重要的不是开发，而是转变教师的教学方式，丰富学生的学习方式. 我们要以课堂教学为主阵地，以加强学生的思维训练为突破口，全面提高学生的数学素养，拓宽学生的思维空间，使课堂焕发出无限的精彩和活力.