持续有界路面激励下的车辆主动悬架可靠L1干抗抑制控制

王 刚，陈海虹，周知进

（贵州理工学院 机械工程学院，贵阳550003）

悬架系统是汽车底盘的重要机械部件，其功能为支撑车身重量并提供必要的舒适性、平顺性。随着传感技术、控制技术的发展，开发智能可控的主动悬架是当前的发展趋势[1–4]。

在主动悬架控制算法的研究中，H∞控制是一个有效的控制方法，已经取得了大量的研究成果[5–18]。由于悬架性能的多样性，研究主动悬架的多目标控制是有效的解决方案。在现有的H∞控制或H∞/GH2控制中，以L2增益来衡量舒适性的好坏，同时以GH2性能来保证悬架行程和轮胎动载荷不超过给定的界限。该方案由于便于处理多目标控制问题，得到了广泛的关注，如采样的H∞控制[5–6]、有限频域H∞控制[7–8]、状态微分和时延容错的H∞控制等[9–18]。另一方面，执行器可能因为老化、部件磨损、外部干扰等因素导致出现输入效率损失，即执行器错误[12]。

然而，值得注意的是在主动悬架的H∞或GH2控制中，路面激励假设为能量有界的外部干扰（L2空间）。由于持续的随机白噪声路面激励是一类能量无界但是幅值有界的信号，L2增益控制理论上无法应用于干扰为能量无界的情况[11]。如文献[20]研究了持续有界干扰下的二维系统的l∞-增益（L1）问题，在时变时延和持续有界干扰下，取得了良好的控制效果。文献[21]应用l∞-增益理论研究了持续有界干扰下的模糊控制问题。

当前，L1干扰抑制控制得到了一定的关注[19–22]。由于L1干扰抑制能处理幅值有界的持续随机信号，无需假设路面干扰能量有界，能应用于更广泛的路面工况。研究主动悬架的L1干扰抑制控制具有一定的新颖性。

基于上述分析，提出车辆主动悬架的可靠L1干抗抑制控制。给出控制器设计的充分条件，能应用于含执行器错误和持续有界的路面情况。最后，通过3 类典型的持续有界路况验证所提方法的有效性。在不同类型的路面激励下，所提方法具有较好的减振性能。

1 主动悬架模型

研究图1所示的1/4主动悬架模型，图中ms表示簧载质量，mu表示非簧载质量。主动悬架部分由弹簧、阻尼器和主动执行器构成，其中ks和cs表示弹簧刚度和阻尼器阻尼系数，u(t) 表示主动控制力。将轮胎简化为弹簧和阻尼形式，可压缩系数为ku，阻尼系数为cu。定义zs为车身垂直位移，zu为非簧载质量垂直位移，zr为路面垂直干扰。

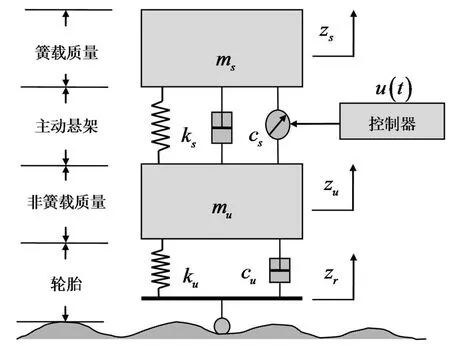
图1 1/4车主动悬架模型

根据图1可得悬架的动力学方程同文献[2]。选择系统的状态矢量为

其中：

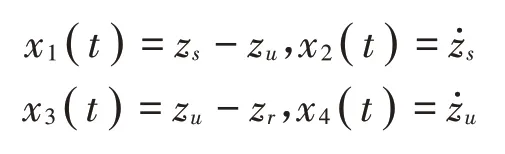
其中：zmax为最大的悬架行程，(ms+mu)g 为整车静载，umax为最大输出力。

为了满足上述要求，定义被控输出及归一化的时域约束为

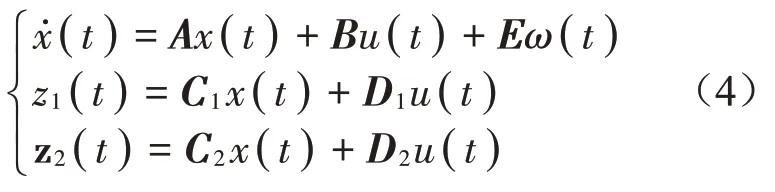
其中：ω(t)表示持续的有界干扰，即ω(t)并不随时间收敛到零点。

对于上述持续的有界外部干扰，定义一个二次型Lyapunov函数和一个L1干扰抑制控制器

其中：F 表示一个1×4 的一般矩阵，P 表示一个4×4的对称正定矩阵。

备注1：H∞及GH2性能指标分别表示如下

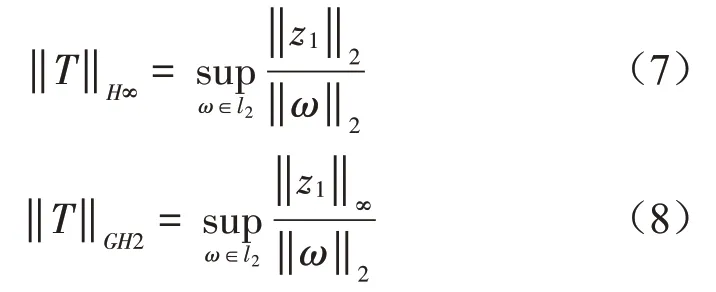
其中：

从式（7）和式（8）可看出，两者都要求路面干扰满足能量有界。因此，并非适用所有路面情况。

在本文中，控制目标为

(1)当ω(t)=0，系统满足指数稳定性。

(2)在零初始条件下满足如下的L1性能

值得注意的是，在设计目标中，仅要求外部干扰是幅值有界的，这符合实际的路面情况。

为了便于证明，引进如下引理。

引理1（Tseng[21]）：给定标量α、β，可微的实标量函数以及干扰若有则如下不等式成立

2 可靠L1干扰抑制控制

如下定理以LFMIs形式给出了可靠L1干扰抑制控制器的存在条件，主要结果如下。

定理1（L1干扰抑制控制）：考虑闭环系统(4)，给定正标量α、β、ϑ、ρ，则系统在无摄动时满足指数稳定性，且在零初始条件及最大干扰幅值ωmax=ρ下满足悬架硬约束（2）及L1性能指标（9）。若存在对称矩阵P>0和一般矩阵F满足

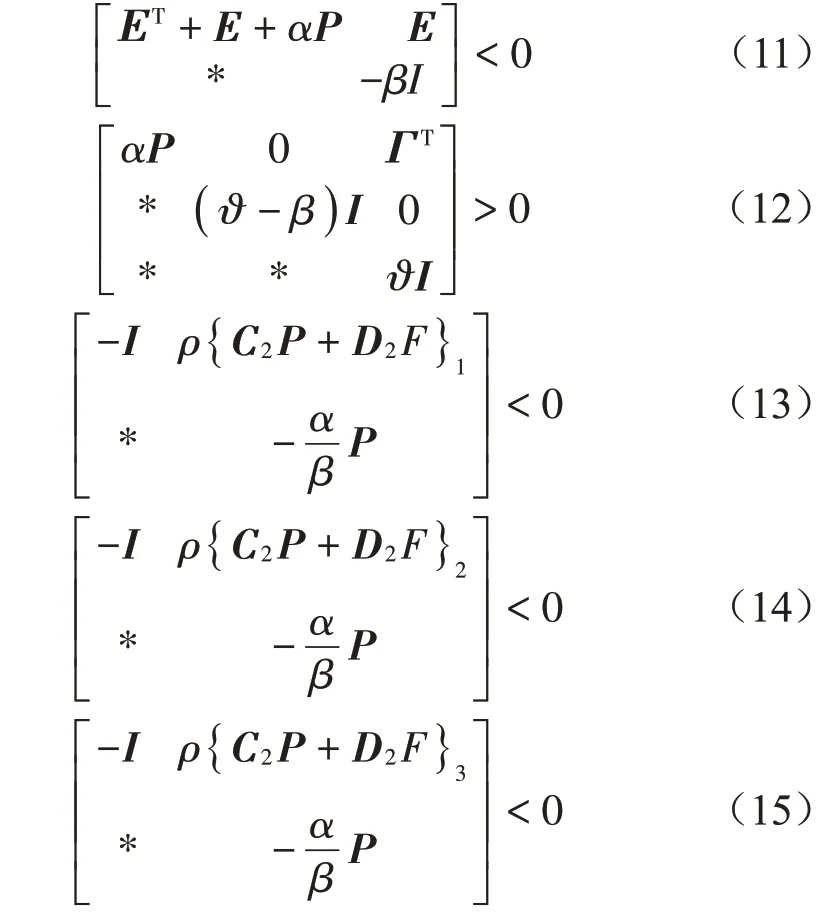
其中：Ε=AP+BF，Γ=C1P+D1F，*表示对角对称项。

证明：对二次型Lyapunov函数式（5）求导可得

进一步代入系统微分方程及L1干扰抑制控制器可得

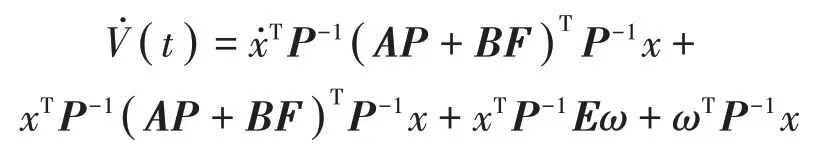
上式可改写为

在上式两边加上αxTP-1x-βωTω可得

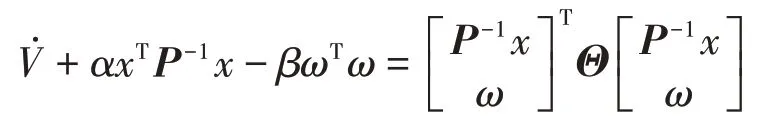
其中：

若满足式（11），可保证Θ负定，则有

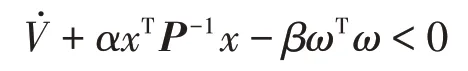
在无干扰下，由Lyapunov 不等式V+αV <0 可知系统满足指数稳定性。

在持续的有界干扰下，根据引理1可知

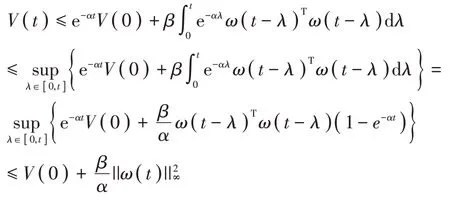
在零初始条件下可得

其中：ωmax=ρ2。

为了满足系统的L1干扰抑制性能，考虑如下不等式

根据上式可得

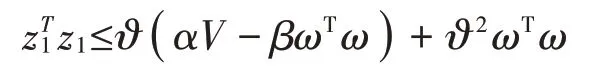
结合式（4），将式（17）改写为

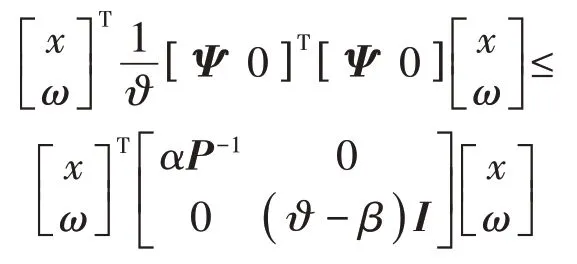
其中：Ψ =C1+D1FP-1。因此，可得

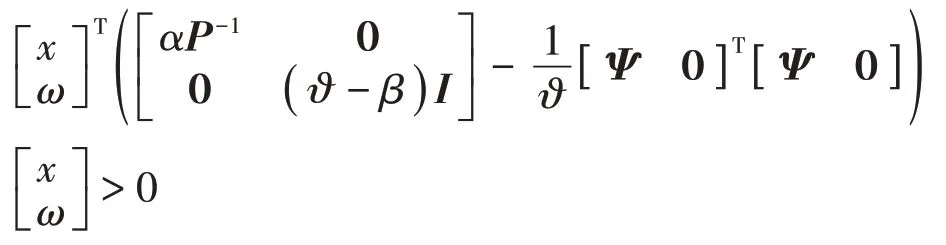
应用Schur-补可得

将悬架硬约束性能写为

应用Schur-补可知上式等于

若满足式（13）、式（14）、式（15），可保证系统在有界的持续干扰下，即ωmax=ρ2时，满足悬架硬约束条件。故证明完成。

备注2：定理1 仅考虑了完美的执行器，即无控制错误。然而在实际控制中，执行器可能因为老化、部件磨损、外部干扰等因素导致出现输入效率损失，即执行器错误[12]。

考虑可能出现的执行器错误，则实际的控制器为

定义

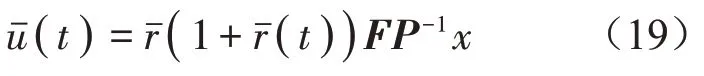
为了设计一个可靠的L1干扰抑制控制器，提出了以下定理。

定理2（可靠L1干扰抑制控制）：考虑闭环系统(4)，给定正标量α、β、ϑ、ρ、ε，则系统在无摄动时满足指数稳定性，且在零初始条件及最大干扰幅值ωmax=ρ 下满足悬架硬约束（2）及L1性能指标（9）。若存在对称矩阵P>0和一般矩阵F满足：

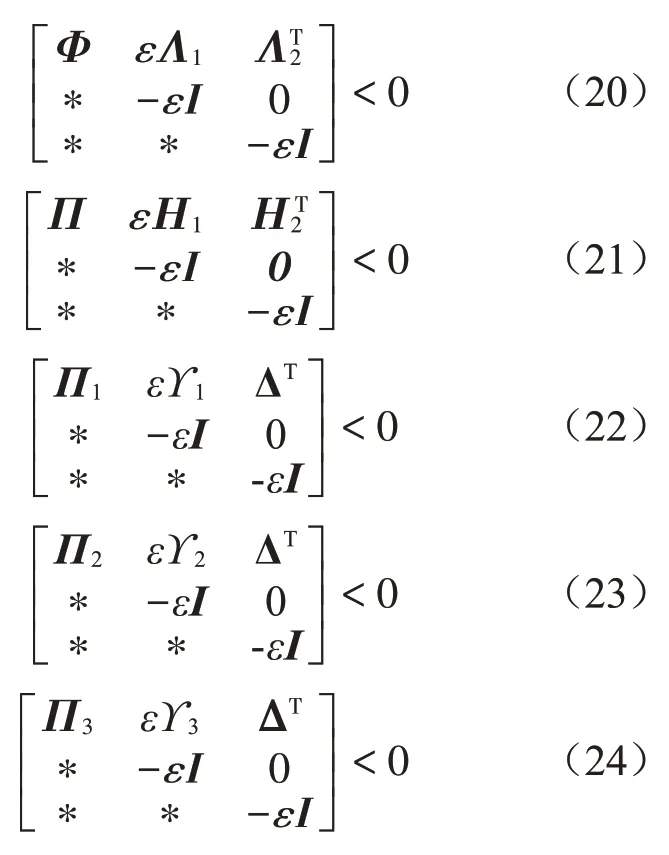
其中：

类似地，可得式（21）至式（24），故得证。

3 车辆主动悬架可靠L1控制研究

本小节研究车辆主动悬架L1干扰抑制性能，在simulink软件里建立主动悬架的控制模型，悬架的参数如表1 所示[23]。悬架行程约束选为zmax=0.1m，最大控制力为umax=2 500 N。

假设执行器存在部分失效，执行器错误满足rm=0.8，rM=1。r(t)在rm和rM之间随机变化。由于定理2 含有线性-分数矩阵不等式，需要对控制参数进行线性搜索来寻找最优解。参数的搜索范围为0<α<10，0<β<10，搜索间隔为0.1。优化的控制参数为α=2.9，β=7。假设路面激励的最大幅值的平方为ωmax=0.01，故可取ρ=0.1。

表1 1/4车模型参数

为了评估闭环系统的干扰抑制性能，以3 类典型的持续有界的路面轮廓进行验证。

第一类持续的路面轮廓为如下凸起的干扰激励[23]

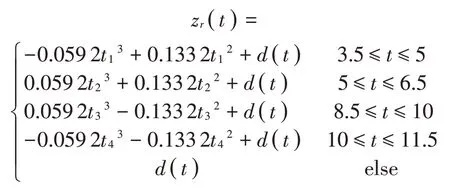
其中：

图2为主动悬架系统在连续包块激励下车身加速度的时域响应曲线。

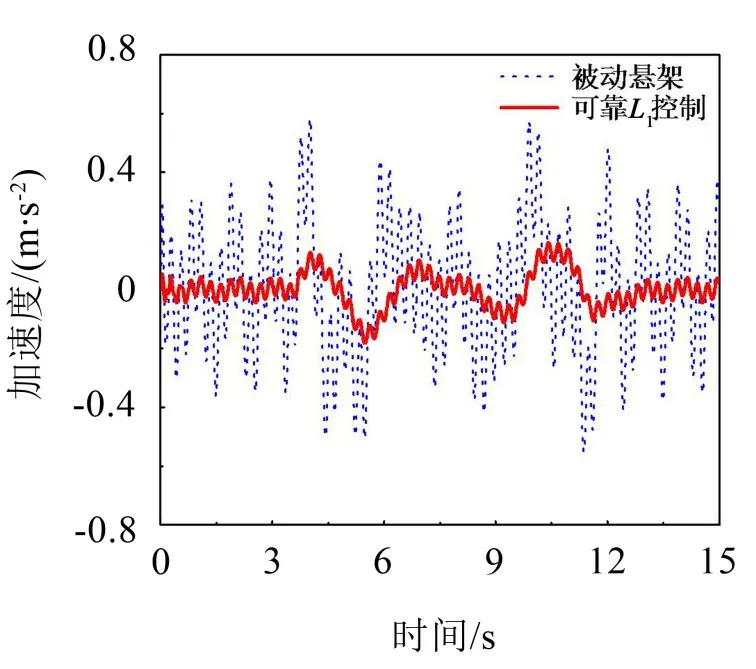
图2 包块轮廓工况下车身加速度响应

图3 包块轮廓工况下悬架约束响应

图3为主动悬架时域硬约束条件下的响应情况。

从图中可看出，在设计的L1干扰抑制控制器作用下，悬架加速度明显小于无控的情况。其中主动控制的车身加速度均方根值为0.06，而被动悬架的车身加速度均方根值为0.229。在进行主动控制时，车身加速度均方根值下降76%。显然，驾驶舒适性能提高了。

第二类持续的路面轮廓为如下正弦型干扰激励[23]

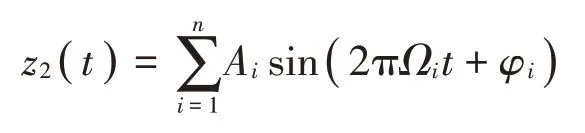
其中：Ai、Ωi和φi分别表示幅值、波数和相位。

在本小节，路面仿真参数取

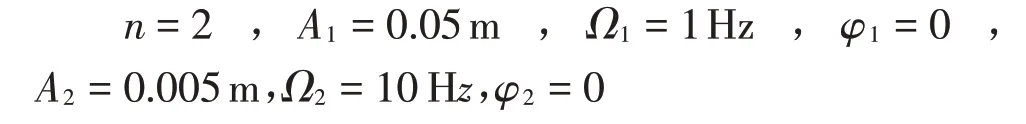
在这种路况下，设置优化的控制参数为：α=2.9，β=7，ρ=0.2。图4 为主动悬架系统在正弦型道路激励下车身加速度的时域响应曲线。

图4 正弦型路面轮廓工况下车身加速度响应

图5为主动悬架时域硬约束条件下的响应情况。从图中可看出，在正弦型道路激励下，悬架加速度明显小于无控的情况。其中主动控制的车身加速度均方根值为1.289，而被动悬架的车身加速度均方根值为2.996。在主动控制条件下，车身加速度均方根值下降57%。显然，驾驶舒适性能提高了。在正弦型道路激励下，最大的干扰界限ωmax<ρ2，故悬架动行程、轮胎动载荷和控制力均小于给定的极限值，而被动悬架的悬架动行程超出了规定的范围。

图5 正弦型路面轮廓工况下悬架约束响应

第三类持续的路面轮廓为如下随机干扰激励[2]

具体符号定义可详见文献[2]。w(t)表示单位功率谱密度的零均值白噪声，其余参数为

图6为主动悬架系统在连续随机激励下车身加速度的时域响应曲线。

图7 为主动悬架时域硬约束条件下的响应情况。由于持续的随机白噪声路面干扰不满足能量有界条件，故L2（H∞/GH2）干扰抑制控制器理论上无法应用。而本文提议的L1干扰抑制控制器能够处理能量无穷的持续随机白噪声路面。

图6 随机路面轮廓工况下车身加速度响应

图7 随机路面轮廓工况下悬架约束响应

从图中可看出，在设计的L1干扰抑制控制器作用下，悬架加速度明显小于无控的情况。

其中主动控制的车身加速度均方根值为0.132 3，而被动悬架的车身加速度均方根值为0.514 2。在主动控制时，车身加速度均方根值下降75%。显然，驾驶舒适性能提高了。同时，悬架约束性能也能得到满足。

图8 为悬架加速度的频域响应曲线，从图中可知L1控制在0.1 Hz～100 Hz范围内能有效抑制外部干扰的影响，且ρ越小，干扰抑制效果越好。

表2 为ρ 不同时的车身加速度均方根值，由于ρ反映最大的干扰幅值，故可根据路面情况进行设定。当路面等级较大时，选择较大的ρ 值。当路面等级较小时，可选择较小的ρ。为了保证悬架硬约束，有时需要较大的ρ。同时注意到参数α 和β 也会影响系统的干扰抑制性能，故可预先进行控制参数线性搜索来寻找最小的L∞范数。

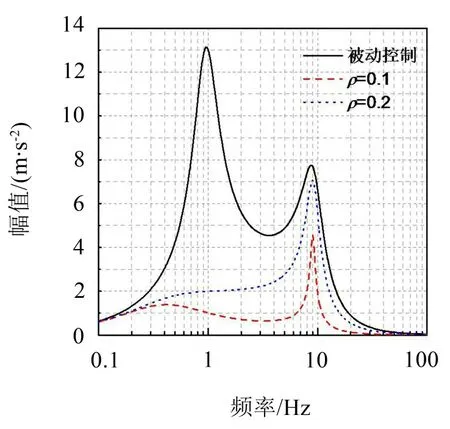
图8 悬架加速度频域响应

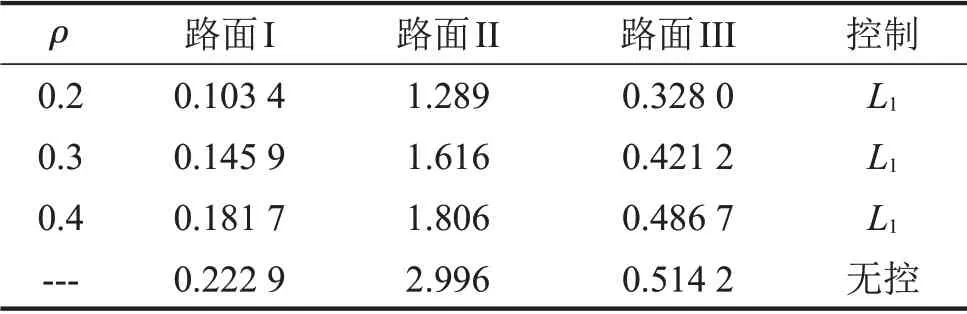
表2 ρ不同时的车身加速度均方根值

4 结语

提出可靠的L1干扰抑制控制器设计方法，用于车辆主动悬架的多目标控制。相对于基于H∞/GH2的控制方法而言，所提方法的优点在于移除了路面干扰能量有界的假设，可适用于持续有界的路面干扰。在控制中，将设计条件归结为一个广义特征值问题，可方便应用标准的数值软件进行求解。

数值结果验证了设计方法的有效性，在持续有界的路面干扰和执行器部分失效工况下，可靠的L1控制方法能明显提高驾驶舒适性能，且保证时域硬约束性能。研究结果能够为主动悬架的L1控制提供一定的理论参考依据，在后续的研究中，可进一步将结果推广到考虑参数摄动及含执行器时延的可靠的L1控制。