基于频响函数的结构损伤识别模型修正方法

殷 红，马静静，董小圆，彭珍瑞，白 钰

（兰州交通大学 机电工程学院，兰州730070）

模型修正在复杂工程结构的损伤识别中有着非常重要的作用。目前设计参数型有限元模型修正（Finite element model updating，FEMU）方法应用广泛，主要有基于频响函数（Frequency Response Function，FRF）的模型修正和基于模态参数的模型修正[1]。和后者相比，基于FRF 的FEMU 不需要模态识别，避免了在模型修正过程中引入识别误差，并且FRF能够提供更多的数据，适用范围更广[2]。

在模型修正中建立灵敏度方程时，要求实测自由度数等于有限元模型的自由度数，而通常实测自由度数远远少于有限元模型的自由度数，这就导致有限元模型与试验所测的自由度数目不匹配。通常用试验模态扩展方法[3]和有限元模型缩聚方法[4]来解决此问题，然而这些方法往往会让有限元模型修正变成非线性优化问题[5]。为了得到准确的结果，建立线性灵敏度方程是非常需要的。文献[6]用损伤结构的固有频率近似计算未测量的FRF 数据。此外，目前把模型修正与损伤识别相结合的方法引起了学者的广泛关注。文献[7]用模型修正理论对桥墩进行损伤定位与定量评估。文献[8]提出了一种基于FRF 模式置信准则的改进模型修正方法，用以识别结构的损伤指数。

FEMU 的结果往往受多种因素影响，除了建立准确的灵敏度方程外，测点位置的选择也是FEMU必须解决的关键问题，而且，选择合适的频率范围也对FEMU 的结果有着重要影响。基于此，本文用FRF 摄动分析法建立FRF 灵敏度方程，研究如何选择频率范围以及解决测试信息不完备问题，然后提出针对于频响函数模型修正的传感器优化布置方法，确定传感器的数目和位置，最后通过给桁架结构设定损伤工况来验证该模型修正方法的有效性。

1 基于频响函数的模型修正方法

1.1 位移频响函数

一个具有比例阻尼的多自由度系统，激励向量为f，位移响应向量为x。在外部激励作用下的运动微分方程可以表示为

式中：M、K和C分别表示质量矩阵、阻尼矩阵和刚度矩阵。对式(1)进行傅里叶变换，可得

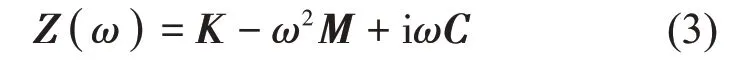
Z(ω)的逆矩阵即为位移频响函数矩阵

则位移频响函数即为响应与激励傅氏变换之比

位移频响函数可以写成如下模态叠加的形式，从而可以通过系统模态参数来计算频响函数。

式中：ωg为第g阶无阻尼固有频率；ξg为模态阻尼系数；ϕgp和ϕgq分别为第g 阶模态在节点p 和节点q 的振型幅值；Hpq(ω)为频响矩阵H 的第(p,q)元素，表示在第q自由度施加简谐激励时，第p自由度上的位移响应；r表示模态数目。

1.2 基于频响函数摄动分析的模型修正

利用结构实测频响函数和有限元计算得到频响函数间的差值构造如下目标函数

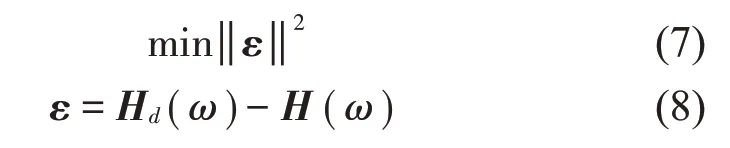
式中：ε 和Hd(ω)分别为测量得到的结构位移频响函数和根据有限元分析得到的位移频响函数；ε 为频响函数残差向量。

当结构出现损伤时，结构特性和响应会随之发生改变，为了避免由对频响函数的求导和运用1 阶泰勒级数所引起的复杂运算，用摄动法建立灵敏度方程，损伤结构位移响应的傅里叶变换为

损伤结构的频响函数矩阵为

式中：δM、δC 和δK 分别表示损伤结构质量、阻尼和刚度矩阵相对于完好结构的摄动量。

将式(10)代入式(9)可得

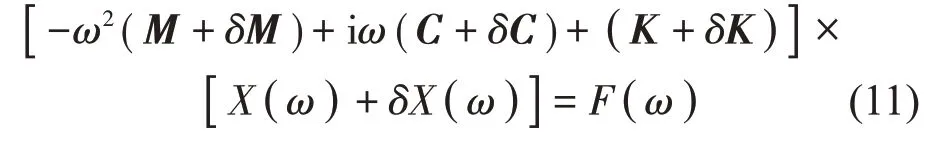
将上式展开并从中求出δX(ω)，得到

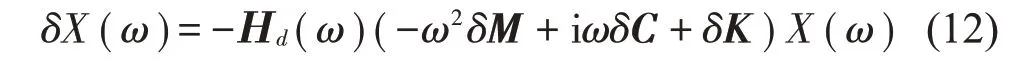
将式(5)和式(9)代入式(12)，并消去F(ω) ，可得

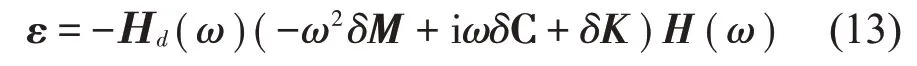
式(13)可准确地修正结构质量和刚度参数，因为它实质上是一个关于结构参数变化量的线性函数。目前大多数阻尼模型不能很准确地去模拟实际阻尼效应，反而会增加模型误差，影响模型修正结果，所以本文中不对阻尼参数进行修正。

其中，结构总体刚度矩阵的变化可由各刚度修正单元的偏微分之和来表示

同理，结构总体质量矩阵的变化表示如下

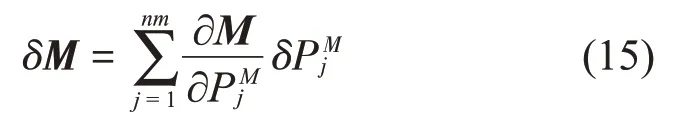
将式(14)、式(15)代入式(13)，并忽略对阻尼参数的修正，即δC=0，可得

式(16)可以改写为如下矩阵相乘的形式

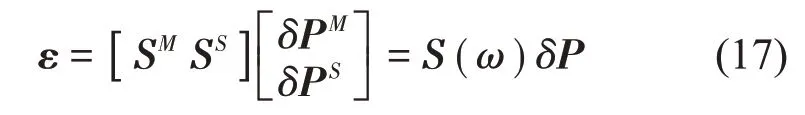
式中：δPM为质量参数灵敏度矩阵，δPS为刚度参数灵敏度矩阵。δPM和δPS分别为质量参数和刚度参数的变化量，δP 为所有修正参数的变化量。S(ω)表示总体灵敏度矩阵。

在实际测试中，方程组(17)通常是不适定的，其最小二乘解为

式中：S+=[S(ω)TS(ω)]-1S(ω)T。最小二乘法的解主要由数值系数较大的部分方程决定，也就是说有些方程可能会掩盖其他方程的信息。所以，通常选用适当的正则化方法来减小灵敏度矩阵的条件数[9]，进而降低灵敏度矩阵的病态性，减少其对模型修正结果的影响。本文中采用相应行的2-范数对灵敏度矩阵的每一个行向量进行归一化。

1.3 估计损伤结构的FRF

由式(13)建立模型修正的灵敏度方程时，要求实测自由度数等于有限元模型的自由度数，而通常实测的自由度数远远少于有限元模型的自由度数。

图1 是结构在完好和损伤状态下的FRF 曲线，从图中可看出当激励频率位于结构的共振区周围时，损伤将导致FRF沿着坐标轴有一定的移动，但形状并没有发生明显的改变。分析表明，在不同的共振区完好状态FRF曲线与损伤状态FRF曲线的平移距离不同。因而可以先测量各共振区内的平移量，再将完好状态FRF曲线通过平移得到损伤状态FRF曲线的近似估计。

因此，在共振区附近Hd(ω)的近似估计可表示为

其中

式中：Ωdn和Ωn分别为完好结构和损伤结构的第n阶固有频率，δΩn表示完好结构和损伤结构间的频率变化量，m表示测量得到的损伤结构固有频率的阶数。图1显示了这种估计的过程。

建立灵敏度矩阵时用的是无阻尼的H(ω)和估计得到的Hd(ω)，但是为了模拟阻尼对算法的影响，用有阻尼的Hd(ω)和无阻尼的H(ω)来计算残差向量ε。在之后的迭代计算中，完好结构的结构参数将不断地更新，逐渐趋近于损伤结构的参数，因而，式(19)和式(20)中，初始Ωn和H(ω)将不断迭代更新，向损伤结构的固有频率和频响函数不断收敛。

图1 结构在完好和损伤状态时第n阶固有频率附近的FRF

2 模型修正频率范围选择

频率的合理选择能提高有限元模型修正的精度和收敛性。图2 是在整个频率范围内，结构受到激励时所有测点自由度响应的灵敏度矩阵的2-范数图。范数的值越大，表明结构参数发生变化时，其FRF的灵敏度越高。

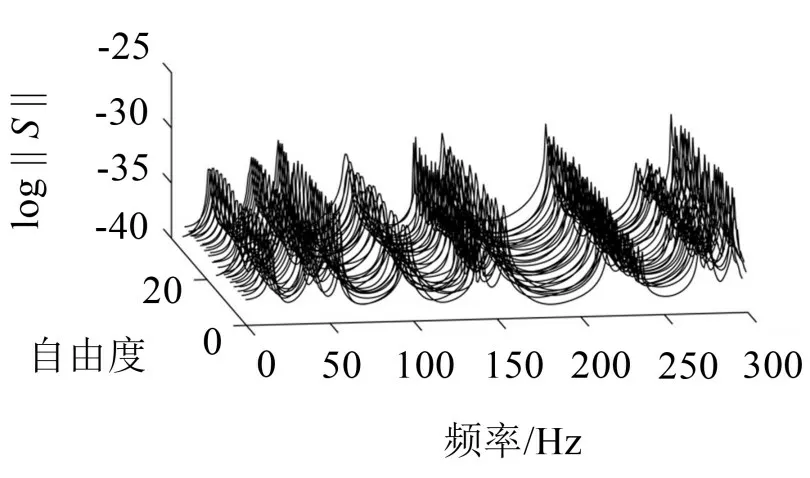
图2 完整频率范围内结构单点激励时所有测量点灵敏度矩阵的2-范数

从图2 可以看出，结构的FRF 在远离共振频率时对结构参数的变化不敏感，而在共振频率附近具有良好的灵敏度，所以选共振频率附近的频率点进行模型修正。

本文没有对阻尼参数进行修正，所以要减小结构阻尼对模型修正结果的影响。由于阻尼在共振区内对振幅的影响很大，当远离共振区时影响迅速减小，因此所选择的频率范围应与共振点保持一定距离，在每次迭代中，始终排除共振点周围约4 Hz 以内的频率范围。

若2 个相邻的共振峰距离太近，则其之间的频段内不能保证FRF 的变动量在修正过程中单调下降，因而排除该区域，以避免振幅非线性问题[10]。在每次迭代时，频率范围还需根据共振点的变化进行调整。

3 模型修正测点选择

在模态测试及模型修正中，有效独立法（Effective independence，EFI）被广泛应用于确定传感器测点。后来，Kammer[11]提出了频率响应有效独立 法（Frequency effective independence，FEFI）。FEFI的主要步骤如下：

(1)在目标频率范围内，利用有限元分析得到结构固有频率和振型计算频响数据矩阵

式中：H(ωi)∈Cns×na为频率ωi处的频响矩阵，i=1，2，…，f 表示采样频率点，f 为频率点总数，ns和na为传感器数目和激励点数目。

(2)对频响数据矩阵进行奇异值(SVD)分解，对模型进行降维和去噪。D经SVD分解后表示为

式中：U 是一个ns×ns维的复正交矩阵，它相互正交的列向量也称为主方向；S 是由奇异值组成的对角矩阵；V是一个na×na维的复正交矩阵，它的行向量表示相应主方向上归一化的频率响应。频响矩阵的各主方向同时满足

式中：U∈Cns×na和V ∈Cns×na为酉矩阵，对角阵S 对角线上的元素即为奇异值。U相互正交的列向量也称为主方向；V 的行向量表示相应主方向上归一化的频率响应。频响矩阵的各个主方向满足关系。式中：上标*表示共轭转置。由于奇异值的大小反映了系统的总能量在相应主方向上的分布，因此，将奇异值按降序排列，去除接近于0的奇异值，进行主成分分析，保留占系统总能量95%～99%的主分量，实现降维和去噪，同时保留系统中的真实模态信息。

设 U=[u1,u2,…,uns]，V =[v1,v2,…vna]T，S=diag(σ1,σ2,…,σr,0,…,0)。其中，us∈Cns×1，σi是D的奇异值，若选前l 个分量进行重构，则H 可近似表示为

式中：DD为D的主分量。

(3)根据主成分分析，将U中保留主方向的列向量组成的矩阵记为ψ。参照EFI，频响数据矩阵可表示为主方向上的频率响应与独立同分布高斯白噪声的和。记高斯白噪声为N，则有

其中：ψ表示相应主方向上的频率响应。根据Fisher信息矩阵推导可得

以信息矩阵的行列式作为目标范数，计算有效独立分布向量

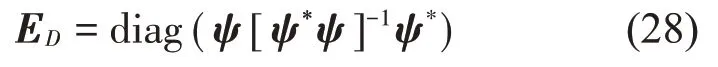
ED中越小的元素表示对应的候选测点对目标模态分量线性独立性的贡献越小，应该首先剔除，依次迭代，直至候选测点数目为所需要的传感器数目为止。

由文献[12]可知，采用EFI 选择测点时，若传感器数目大于目标模态数目，测点可能在局部聚集，从而导致信息冗余。由于FEFI 是EFI 在频域内的推广，具有与EFI 相同的性质，因此，分两步为模型修正选择测点位置。首先采用FEFI 确定与主方向相等数目的测点位置；然后采用文献[13]中的距离系数—有效独立法，确定传感器的数目。该方法以距离系数修正Fisher信息矩阵，避免了EFI中信息冗余的问题。迭代中以使修正后的Fisher信息矩阵行列式最大化来逐步增加传感器布置节点，直到布置的传感器采集的信息能够得到可靠的模型修正结果。

算法的流程如图3所示。

图3 模型修正流程图

4 数值模型试验

4.1 模型简介

图4 桁架结构的单元及尺寸/cm

图4所示的平面桁架结构由40 个杆单元组成。每个杆单元的密度为7 800 kg/m3，弹性模量为200 GPa。1－9号单元、10－18号单元、19－26号单元以及27－40号单元的横截面积分别为18 cm2、15 cm2、10 cm2和12 cm2。结构有18 个节点，33 个自由度，如图5所示。

图5 桁架结构的自由度

这里用0.5%的阻尼系数来模拟模型的实际阻尼，选择单元轴向刚度EA 作为待修正参数，E 为弹性模量，A为横截面积。设定2种损伤工况来验证模型修正方法的有效性，在工况1中，预设第7、10、17、23 和30 号单元为损伤单元，其刚度分别下降20%、20%、20%、30%和30%；工况2中，预设第15、25和38 号单元为损伤单元，轴向刚度分别下降30 %、40%和30%。假设结构受单点激励，激励点分别选择在第2、16、19、29 和33 自由度处。对以上2 种损伤工况进行有限元分析，得到损伤结构的固有频率和频响函数。

4.2 选择频率范围并估计损伤结构的FRF

分别对完好结构和损伤工况1 这2 种工况下的结构在第2 自由度处进行激励，第13 自由度上采集输出信号，分析得到无阻尼频响函数曲线如图6所示。

图6 结构在完好状态和损伤工况1对应的FRF

可以看出，在共振区完好结构和损伤结构的频响函数差异变大，再结合第2小节的规则，模型修正的频率选择为共振区附近的频率点。去除含有前3个共振区的低频段；为避免振幅非线性的问题，忽略第5和第6共振区之间以及第7和第8共振区之间的频率点。

选取结构的前8阶固有频率，根据以上分析，采样间隔为1 Hz，工况1和2中分别选择的频率范围如表1所示。

表1 用于模型修正的频率范围

根据上面选择的频率，采用1.3小节的方法对相应的FRF 进行估计。图7 为损伤工况1 下结构的精确FRF曲线以及在所选频段内估计的FRF图。从图7 中可以看出FRF 的估计值高度近似于FRF 的精确值。

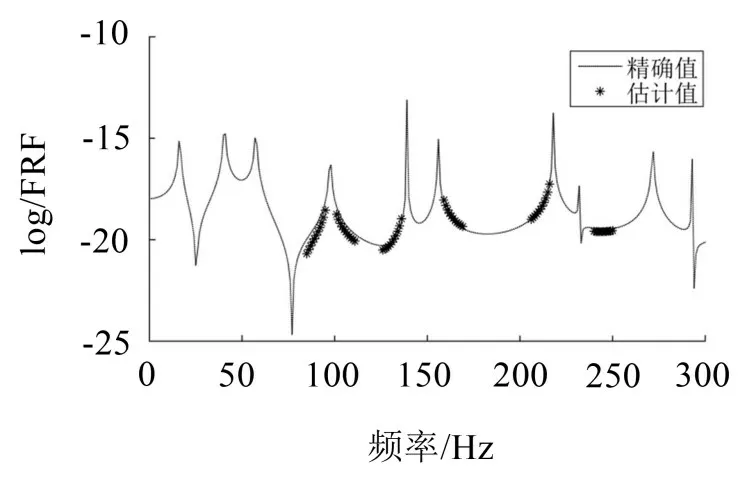
图7 工况1下精确的FRF以及在所选频段内估计的FRF

4.3 测点优选

根据FEFI的算法思想，分两步完成测点优选。

第一步，初选感器布置位置。

根据4.2 小节确定的频率范围计算频响数据矩阵D。对D 进行SVD 分解，降维后保留前5 个奇异值，让主方向上的能量占到系统总能量的95%。由式(28)计算有效独立分布向量,在迭代中逐次剔去其中最小元对应的候选测点，直至候选测点减少至5个时停止。迭代结束时确定初选测点为第3、10、17、19、33自由度。

为了和采用距离系数—有效独立法优化测点位置后的效果相比较，在进行下一步之前，在此先取初选测点进行模型修正，得到结构损伤识别结果。

针对工况1，在这5 个初选自由度上布置传感器，进行基于FRF 的FEMU，损伤识别结果如图8所示。

由图8 可看出，对第7、10、17、30 单元的损伤识别较准确，对第23 单元处的损伤程度识别较差，同时对第5、20、21、22、33 等单元处出现了损伤误判。说明在初选测点下直接进行模型修正虽然可以对大多数实际损伤位置进行识别，但同时会在其他位置上出现误判断和欠判断的情况。由于损伤识别结果不能很好地反映实际工况，在此不再对工况2 进行试验。

图8 布置5个传感器时模型修正识别的损伤和工况1实际损伤

第二步，采用距离系数—有效独立法增加测点位置。

为了改善损伤识别效果，可逐步增加结构中布置的传感器数目，并采用距离系数—有效独立法确定增加的测点位置，得出第6 个测点位置为第25 自由度。针对工况1和工况2，分别在第3、10、17、19、25、33自由度处布置传感器，进行基于FRF的FEMU，损伤识别结果如图9所示。

4.4 模型修正结果分析

从图9可以看出，布置6个传感器时获得的频响数据能识别出工况1和2的损伤程度和位置，且识别结果较为准确。虽然在一些位置出现了虚假损伤，但都很微小，可以忽略不计。这主要是受阻尼和模型修正中估计误差的影响而导致的。

表2 给出了弹性模量的修正结果。可看出，修正后损伤单元的弹性模量和真实值高度吻合，修正结果相对误差的最大值为2.58%。

表3给出了两种损伤工况下固有频率的修正结果。可以看出，修正后的结构前8 阶固有频率和通过有限元分析计算得到的精确值基本一致，最大相对误差仅为0.33%。说明采用本文方法能有效地识别出损伤结构的真实参数，可以提高结构动力学分析的准确性，为后续的优化设计提供依据。

5 结语

(1)建立数学模型时采用摄动法进行灵敏度分析，推导出质量和刚度参数变化与FRF 变化之间的线性关系。避免了使用泰勒展式以及对频响矩阵的求导运算，而且建立的模型修正方程没有截断误差，在参数修正过程中稳定性良好。

(2)分析完整频率范围内结构单点激励下所有测量点灵敏度矩阵的2-范数，合理确定用于模型修正的频率范围。利用测量得到的损伤结构的固有频率和完好结构的FRF 来重构未测量节点上的FRF，解决了测试信息的不完备问题。对灵敏度矩阵的每一个行向量采用相应行的范数进行归一化，提高了算法的稳定性。

图9 布置6个传感器时模型修正识别的损伤和实际损伤

表2 弹性模量修正结果

表3 2种损伤工况下结构固有频率的精确值及修正值

(3)测点的优选决定了损伤识别的精度。采用FEFI 与距离系数—有效独立法相结合的方法来确定传感器布置方案。数值模型试验分析表明，由该方法确定的少量传感器获得的FRF数据就能较为准确地识别损伤，模型修正结果与损伤结构真实参数高度吻合。

虽然数值算例中得到了较为理想的修正结果，但是实际试验中存在环境等不确定性因素，所以，需要进一步研究如何利用实测数据并考虑不确定因素进行模型修正。