磁流变半主动悬挂引入位置阈值的改进Bang-Bang控制

张耀辉，彭 虎，张进秋，孙宜权，张 建

（1.陆军装甲兵学院 装备保障与再制造系，北京100072；2.陆军装甲兵学院 车辆工程系，北京100072）

车辆悬挂系统用以支撑车体，缓和路面不平度激励，起到隔振的作用，其性能对车辆的乘坐舒适性、行驶安全性及操纵稳定性等具有重要影响。半主动悬挂是一类可通过调节执行器的阻尼，可实现以耗散悬挂振动能量为目的的可控悬挂[1]。其中，磁流变半主动悬挂通过改变线圈产生的磁场强度，调节悬挂阻尼，具有响应迅速、易于控制、可靠性好等优点，是一种较为理想的半主动控制执行器，而设计相应的半主动控制算法是提高磁流变半主动悬挂控制性能的关键之一[2]。

随着控制理论的发展，目前，车辆悬挂控制算法主要分为以下4类：

(1)基于车辆状态信息判定的控制算法，主要包括天棚控制、Bang-Bang控制等[3-4]；

(2)基于经典控制理论的控制算法，主要代表为PID控制[5]；

(3) 基于现代最优控制理论的控制算法，包括LQR、滑模控制及自抗扰控制等[6–8]；

(4)无需精确模型的智能控制算法，主要包括模糊控制及神经网络控制等[9–10]。

其中，第一类控制算法计算量小，意义明确，通过采集车辆状态信息进行相应的反馈控制，即可实现对车辆悬挂的控制。简单的Bang-Bang控制算法以判定被控对象位移和速度的方向作为控制依据，当目标偏离平衡位置时，施加大阻尼力以减小偏离的趋势；趋向平衡位置时，施加小阻尼，以减小回归平衡位置时对其的阻碍。该算法的缺点在于会使被控对象在过平衡位置时穿越速度过大，易出现往复振荡现象，影响悬挂性能。

为解决Bang-Bang控制算法使对象在穿越平衡位置时的穿越速度过大的问题，以车身为对象，以车身垂直速度及垂直加速度为输入判定依据，提出一种减小车身过平衡位置时的穿越速度的改进Bang-Bang控制算法。建立相应的综合性能评价指标，分析算法原理及取值方法，并对改进型Bang-Bang 控制算法的控制性能进行仿真及试验验证，探讨其对乘坐舒适性、行驶安全性及操纵稳定性等悬挂性能指标的影响。

1 悬挂模型及评价指标的建立

1.1 悬挂动力学模型

假设某独立悬挂车辆质量分配系数为1，建立被动悬挂及装有MRD的1/4车2自由度悬挂动力学模型如图1所示。

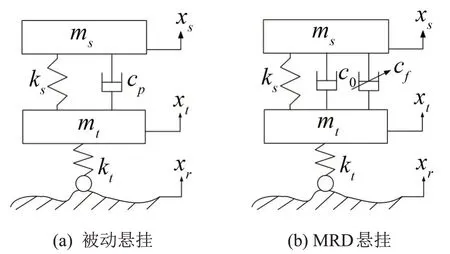
图1 1/4车2自由度悬挂动力学模型

根据牛顿第二定律，运动微分方程为

式中：ms为车身质量；mt为车轮质量；cp为被动悬挂阻尼系数；c0为MRD黏滞阻尼系数；Ff为MRD库仑阻尼力；ks为悬挂等效刚度；kt为车轮等效刚度；xs为车身垂直位移；xt为车轮垂直位移；xr为路面激励垂直位移，以垂直向上为正。

1.2 评价指标

1.2.1 单一指标统计方法

在考察车辆乘坐舒适性方面，ISO2631-1:1997(E)标准给出了车身垂直加速度均方根值与人体舒适性主观评价之间的对应关系[11]。考虑到1 Hz～80 Hz 振动频率范围内，人体对振动反应的界限不同，定义加速度均方根值与人体舒适性主观评价间的对应关系，如表1所示。

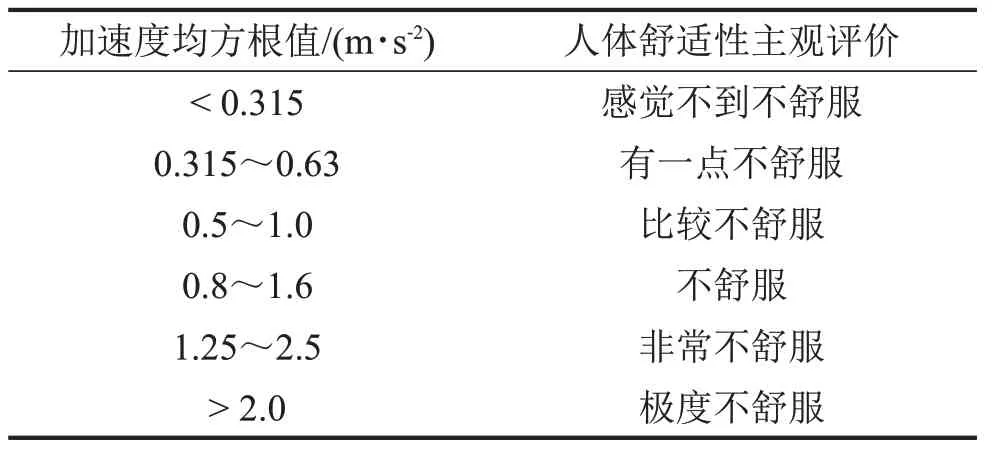
表1 振动量级与主观评价的关系

表1 中有部分重叠的值，为对乘坐舒适性进行较为准确的判断，分别以<0.315 m/s2、0.315 m/s2～0.63 m/s2、0.63 m/s2～1 m/s2、1 m/s2～1.6 m/s2、1.6 m/s2～2 m/s2和>2 m/s2作为主观评价的界定。该表并未涉及车身垂直位移与乘坐舒适性的对应关系，但位移是与加速度相关联的量，因此，可以利用位移与加速度的对应关系，结合表1，建立车身垂直位移与人体舒适性主观评价间的等价关系。

将式(1)中的c0换成cp，并令Ff=0，对其进行Laplace 变换，可得到4 个指标相对于路面输入速度的幅频特性分别为

式中：γ=kt/ks为刚度比；μ=ms/mt为质量比；λ=ω/ωs为频率比为阻尼比；Δ=((1-λ2)(1+γ-λ2/μ)-1)2+4λ2ζ2(γ-(1+1/μ)λ2)2。

分别将式(2)至式(5)表示成速度功率谱形式。由于性能指标的振动响应量均值为零，故性能指标的方差即为均方值。确定了路面不平度系数Gxr(n0)和车速v，即可统计各指标均方根值。从频域角度统计各指标均方根值，通用表达式为

式中：X 可分别表示ACC、DXC、DZH 及DIS。利用式(6)可求取不同路面等级及车速工况下各指标的均方根值。

1.2.2 综合性能评价指标

单一的性能指标仅从某一方面对悬挂性能进行评价，难以反映悬挂的综合性能，需要建立悬挂综合性能指标，以J 表示。以同等条件下的被动悬挂为参考，假设变量为xi(i=1,2,…,N)，其中N 为等份数，每一次计算时的xi均对应、fd(i)及D(i)，设被动悬挂指标为、fd_p(i)及Dp(i)，则可得ACC性能指标JACC为

JDXC与JDZH与JACC的计算方法一致。每个性能指标对应不同的行驶性能，由于不同的车辆及驾驶工况对各个指标的侧重有所不同，因此，考虑用不同的权重对综合性能指标进行加权。假设ACC、DXC及DZH 的权重分别为wj(j=1,2,3)，w1+w2+w3=1。文献[13]提出加权形式包括凹函数、凸函数及线性加权等多种形式，并给出了相应的示例及计算方法。为使指标的改善和恶化权重一致，在此采用线性加权的方式对各指标进行加权求和，综合性能指标J 表达式为

J的值越小，表示悬挂综合性能越优。

2 Bang-Bang控制算法及其改进

2.1 Bang-Bang控制算法

简单Bang-Bang 控制算法以平衡位置为基准，当对象偏离平衡位置时，施加相反方向的力，将其往平衡位置“拽”[14]。而MRD 阻尼只能在大小阻尼之间切换，当MRD可控制力方向与需要的力方向相反时，MRD 输出最小阻尼力以减少对系统运动的破坏；当MRD可提供的控制力方向与需要的控制力方向相同时，则提供最大的阻尼力。以改善车辆乘坐舒适性为目的，以车身为对象，以MRD为执行器，则简单Bang-Bang控制算法的控制逻辑为

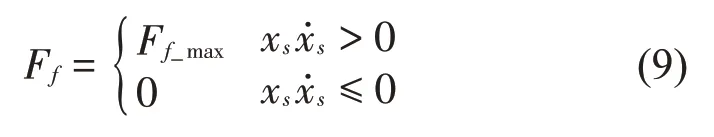
式中：Ff_max为MRD最大库仑阻尼力。

假设激励为正弦激励，xr=A sin(ωt)，简单Bang-Bang控制下MRD阻尼力与位移、阻尼力与速度的关系及正弦时域特征分别如图2、图3 及图4所示。

图2 阻尼力与位移的关系

图3 阻尼力与速度的关系

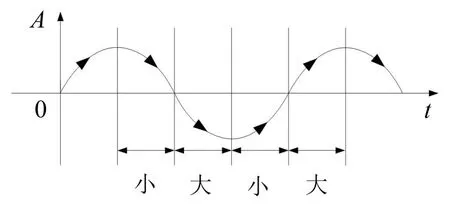
图4 正弦时域特征

由图2、图3及图4可知，在一个周期内，MRD会在大阻尼和小阻尼之间进行4次切换，横轴上xs=0时表示平衡位置，纵轴Fd表示MRD的阻尼力。图2中第一象限内，当xs逐渐沿正向增大，对应图3 的由趋向0，车身垂直向上偏离平衡位置，则施加大阻尼减小偏离的趋势；图2中第二象限内，车体从最上位置回归平衡位置，施加小阻尼，对应图3 内由0趋向；图2中第三象限内，车体向下偏离平衡位置，xs沿负方向增大，施加大阻尼，对应图3内由趋向0；图2中第四象限内，车体从最下位置回归平衡位置，施加小阻尼，对应图3 内由0 趋向根据xs和乘积的方向，即可判定大小阻尼切换的时机，图4 从时域的角度对车身偏离平衡位置的状态及施加大小阻尼的区域进行了描述。从图2 可以看出，大阻尼Fd_max与小阻尼Fd_min切换时，正好处于平衡位置速度最大点，穿越平衡位置时的速度达到最大值，这会形成较大的惯性，给下一阶段的减振减幅带来不利影响。当下一阶段车身偏离平衡位置运动时，阻尼需要克服该部分穿越速度带来的惯性，如果能减小车身过平衡位置时的穿越速度，即可减小惯性，从而改善乘坐舒适性。

2.2 改进Bang-Bang控制算法

2.2.1 改进Bang-Bang控制算法原理

基于2.1 小节的分析，提出如下设想：若能通过设定xs的阈值，在回归平衡位置之前的一小段距离ε以内，提前将MRD 切换到大阻尼状态，则可在该车身垂直位移阈值范围内起到缓冲作用，减小过平衡位置时的穿越速度。由于不同的路面激励、车速及悬挂参数会使车身垂直位移值不同，因此，确定ε的大小是需要解决的一个关键问题，ε 过大会使悬挂始终处于大阻尼状态，不利于车身回归平衡位置；ε过小，又起不到减小穿越速度的抑制作用。

改进Bang-Bang 控制在原Bang-Bang 控制的控制逻辑基础上，除xs区域外，添加位移阈值ε，在 ||xs<ε 区间内，将阻尼设置为大阻尼，以减小被控对象过平衡点时的穿越速度。改进Bang-Bang控制表达式为

式中：ε 为大于0 的小正数，由车身垂直位移均方根值而定。

改进Bang-Bang控制下MRD阻尼力与位移、阻尼力与速度的关系及正弦时域特征分别如图5、图6及图7所示。

由图5 可知，在需要大阻尼的区间，除第一、三象限外还包括第二、四象限xs=±ε区间内的部分，即相当于在车身回归到平衡位置之前，已经加载大阻尼来减小车身达到平衡位置时的速度了。从图6可以看出，简单Bang-Bang控制最大速度为改进Bang-Bang 控制最大速度有效地减小了穿越平衡位置时的速度。

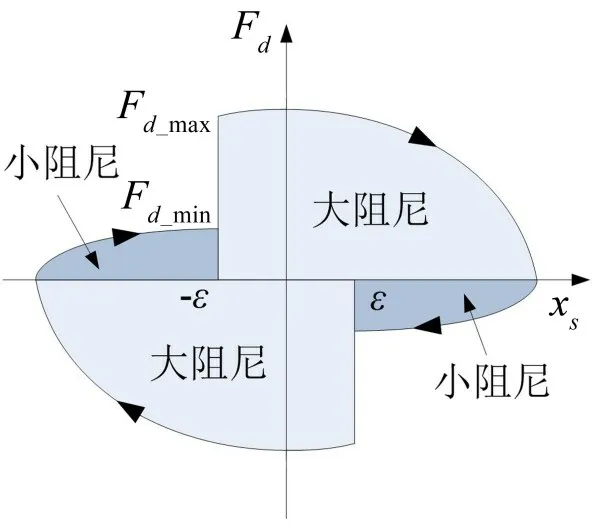
图5 阻尼力与位移的关系

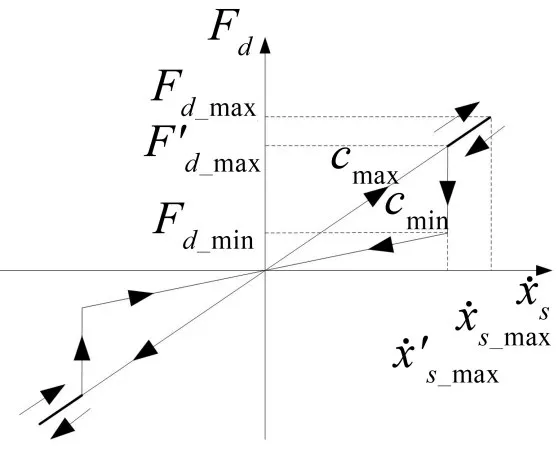
图6 阻尼力与速度的关系

图7 正弦时域特征

由做功公式W =Fd_maxxs可知，若要消耗等量的车身垂直振动功，改进Bang-Bang 控制增大了做功位 移xs，由 ||xs→ ||xs+ε ，等 效 而 言，所 需 的F′d_maxF′d_max，所以，实际的车身垂直位移振动幅度x′s就小于xs，有效地降低了车身垂直振动位移，从而减小车身垂直振动加速度，提高了乘坐舒适性。

实际的车身垂直位移难以直接测量，加速度易于测量，而位移与加速度相位相差π，故在表达式中用替换xs，则式(9)、式(10)分别转化为

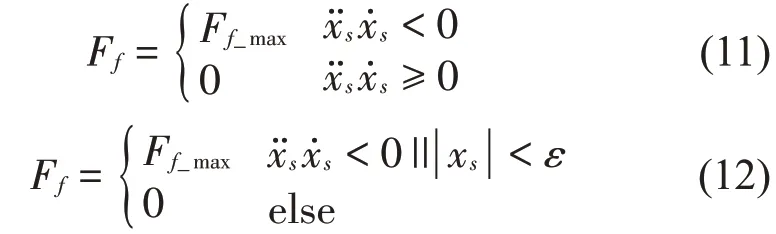
2.2.2 ε的确定方法

1/4车悬挂参数如表2所示。

随机路面激励采用谐波叠加法生成，表达式为

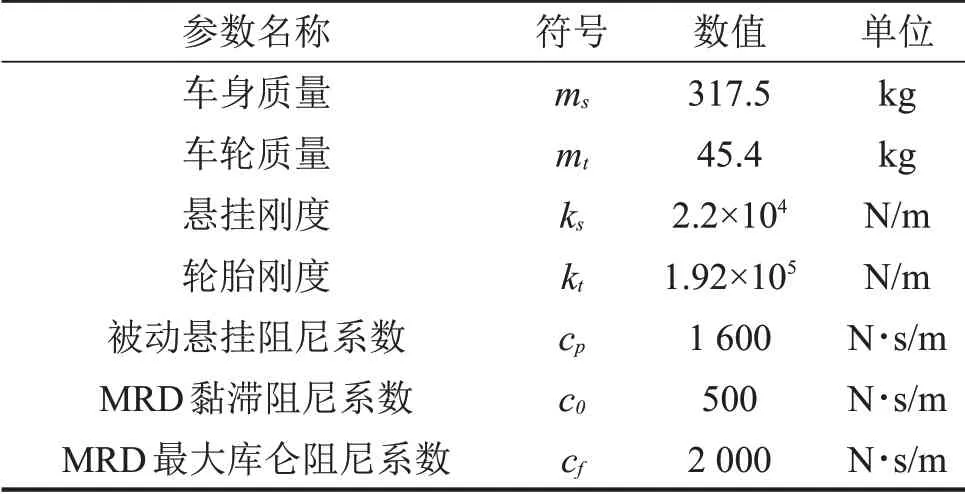
表2 1/4车悬挂参数

式中：φk为[ ]0,2π 上的随机数，且满足均匀分布；fmid_k为频率区间(f1,f2)上第k 个离散区间的中心频率，当车速为v时，fmid_k=nmid_kv；Gxr(fmid_k)为fmid_k处的谱密度值，Gxr(fmid_k)=Gxr(nmid_k)/v。

不失一般性，取D级路面v ∈[0,10]m/s，该路面条件及速度区间包含的各指标值区分明显，但不限于该路面及车速条件。得到ACC及DIS与车速v的关系如图8所示。

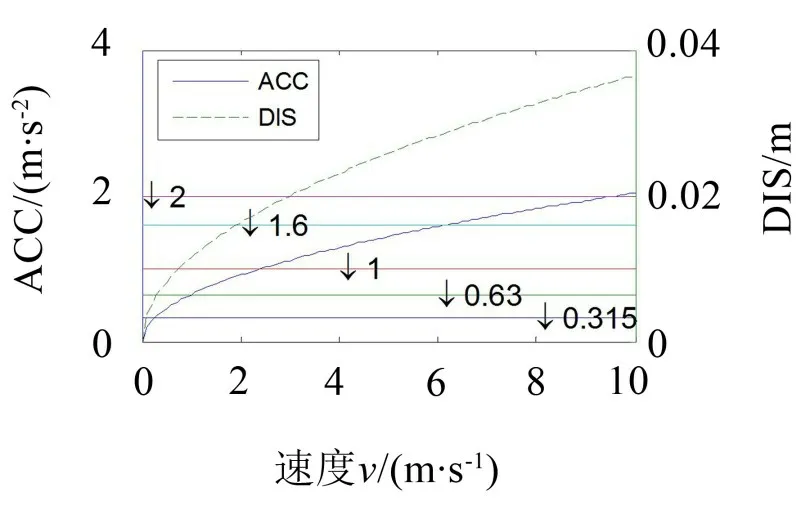
图8 ACC及DIS与车速v的关系

由图8 可得ACC 对应的DIS 值，调整后振动量级与主观评价的关系如表3所示。

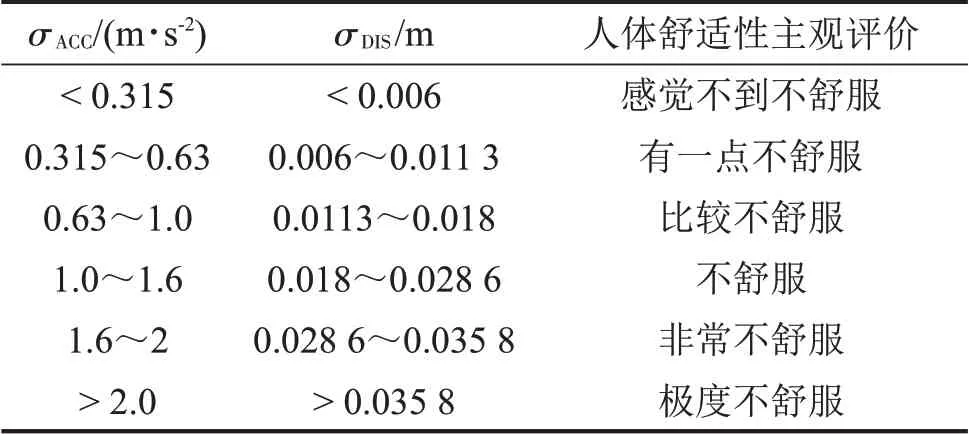
表3 调整后振动量级与主观评价的关系

车身垂直位移阈值ε应当小于位移的均方根值σDIS，不同ε 的取值大小对改进Bang-Bang 控制算法性能的影响不同。为了描述ε与σDIS的关系，引入比例系数λ，表示阈值ε与车身垂直位移均方根值σDIS的取值比例关系，λ的取值影响着改进Bang-Bang控制算法的控制性能，ε=λσDIS，λ ∈[0,1]，λ=0时表示简单Bang-Bang控制。

3 算例分析

以σACC=1m/s2时人体舒适性主观评价“比较不舒服”和“不舒服”为例，对应的σDIS=0.018 m，由图8 可知，σACC=1m/s2时对应条件为D 级路面车速2.4 m/s。分别取λ=0、λ=0.2、λ=0.4、λ=0.6、λ=0.8和λ=1，由于更重视乘坐舒适性（对应ACC），对行驶安全性（对应DXC）及操纵稳定性（对应DZH）的重视程度一样，因此，设定w1=0.6、w2=0.2、w3=0.2。相比于被动悬挂，简单Bang-Bang控制及改进Bang-Bang控制下，对ACC、DXC及DZH的性能提高比率以及综合性能指标J 与λ(同lamda)的关系进行统计，结果如图9所示。

图9 指标性能提高比率及J与lmada的关系

由图9可知，增大λ的值，MRD加载大阻尼的时间占比增大，悬挂变“硬”的时间加长，可使ACC 性能改善幅度逐渐增大，由于ACC、DXC及DZH相互间的矛盾关系，降低ACC 会使DXC 及DZH 均有一定程度的恶化，恶化程度随λ 的增大而增大。综合性能J先减小后增大，在λ=0.6附近取得最小值，因此，在该条件下，选取λ=0.6作为综合性能最优值对应的λ值。

3.1 仿真分析

对该值下的简单Bang-Bang 控制及改进Bang-Bang 控制性能进行时域分析，取悬挂参数如表2 所示，时域分析如图10 所示，指标统计结果如表4所示。

结合图10 及表4 可知，Bang-Bang 控制及改进Bang-Bang 控 制 可 分 别 使ACC 降 低14.11% 和19.72 %，但同时会使DXC 及DZH 有所恶化，改进Bang-Bang 控制的恶化比DXC 及DZH 略大。由于更重视乘坐舒适性，因此，从综合性能指标J 来看，改进Bang-Bang控制优于Bang-Bang控制，人体舒适性主观评价由“不舒服”降为“比较不舒服”，达到了改进优化的目的，该结论与图9分析结果一致。

图10 时域分析

表4 指标统计结果

车身垂直速度如图11所示。

图11 车身垂直速度

相比被动悬挂，Bang-Bang 控制对车身垂直速度并未起到明显抑制作用，改进Bang-Bang 控制有效地降低了车身垂直速度，一定程度上达到了间接抑制ACC、改善乘坐舒适性的目的。

3.2 台架试验

为检验算法的有效性，基于路面谱激励实验台搭建MRD振动控制试验系统，试验系统框图及试验系统分别如图12、图13所示。

位移传感器及车身垂直加速度传感器分别用以采集车辆状态信息xs及xs，将xs微分后即可得到xs；数据采集、控制及MRD电流驱动集成模块组将数据采集板卡、控制板卡和MRD 电流驱动板卡集成，兼具数据采集、控制及MRD 供电的功能；控制上位机用于控制集成模块组，并存储传感器采集的信号；供电电源为各个模块和传感器供电；路面谱激励实验台控制上位机用以对液压激振台进行控制。

图12 MRD振动控制试验系统框图

取与仿真相同的试验参数，指标统计结果如表5所示。

结合表5，对比对应指标的仿真结果可知，Bang-Bang 控制及改进Bang-Bang 控制对ACC 及车身垂直速度的抑制幅度比仿真值略小，总评价指标J 分别 为0.956 8 及0.942 4，改 进Bang-Bang 控 制 比Bang-Bang控制小，综合性能更优。相比之下，DXC及DZH恶化程度也略有增加，这主要是由于仿真模型相比实物做了些许简化以及信号测量及传输存在误差等。但从总体趋势可以看出，改进Bang-Bang控制比Bang-Bang控制具有更好的控制效果。后续将在提高建模、控制精度及数据传输效率方面进行研究，进一步增强工程实用状况下的控制效果。

表5 指标统计结果

图13 MRD振动控制试验系统

4 结语

(1) 通过对ACC、DXC 及DZH 指标的加权，综合性能评价指标J 可根据对3 个指标对应的车辆行驶性能指标的侧重，实现对悬挂性能的综合评价，相比单一的性能指标，综合性能指标更为科学；

(2)随着比例系数λ的增大，ACC性能改善幅度逐步增大，但DXC 及DZH的恶化也逐步增加，综合性能指标先减小后增大，在λ=0.6处取得最优值；

(3) 仿真及试验时域分析结果显示，虽然DXC和DZH 有部分恶化，但对于ACC，改进Bang-Bang控制优于Bang-Bang 控制。从车身垂直速度来看，改进Bang-Bang 控制可显著降低车身垂直速度，改善Bang-Bang 控制穿越平衡位置时速度过大的问题。该改进算法简单易行，适用于车辆工程领域。