自由空间中集群式有源噪声控制系统布放对稳定性的影响分析

玉昊昕，陈克安

(西北工业大学 航海学院 环境工程系，西安710072)

一般来说，集中式多通道有源噪声控制系统在计算馈给次级源的控制信号时，需要使用所有次级通路传递函数的信息和所有误差传感器的信号[1]。集中式多通道有源降噪系统有利于提高降噪量和扩展降噪区域，目前已经广泛运用在各种有源降噪工程中[2]。然而随着次级源和误差传感器数量的增多，实现集中式系统所需要的计算量和成本随之成指数级增长。在实际工程中，可以采用分散式控制策略来降低大规模有源噪声系统的实现难度和成本，分散式系统将集中式系统拆分为多个独立的单通道子系统，每个子系统只有一个次级源和误差传感器，各个子系统独立运行，而不考虑各个子系统之间的声耦合[3]。然而忽略子系统之间声耦合作用将导致系统整体性能的下降并可能导致系统不稳定[4–5]。

集群式系统是一种新的系统实现策略，它介于集中式系统和分散式系统之间，如图1所示。

图1 集群式系统示意图

集群式系统包含多个规模不一的子系统，各个子系统之间虽然互相独立，但子系统本身是一个小规模的集中式系统。

类似的系统在振动或振声控制中也称为分布式（distributed）控制系统。在振声控制的研究中发现某些代价函数下，分散式系统性能显著差于集中式系统，而当使用模块优化和局部代价函数时，分布式系统性能与集中系统一致[6]。而在平板结构的振动控制中，分散式控制虽然能达到与集中式控制相近的性能，但是并不能保证收敛[7]。

与分散式系统相比，集群式系统由于各个子系统更多地考虑了自身次级源和误差传感器之间的声耦合，因此有更好的稳定性[6]；与集中式系统相比，由于子系统规模减小，又大大降低了系统实现难度和成本，是介于集中式和分散式系统之间的折衷形式。

由于常见的噪声可以在频域分解为各个频率，因此本文通过建立集群式系统在单个频率噪声下的理论模型，并将控制迭代公式转换为线性时不变系统传递函数[8]，分析系统布放对传递函数零极点的影响，得出使集群式系统在自由空间中保持稳定的系统布放原则。

1 理论分析

1.1 控制算法

考虑有I个子系统的集群式系统，每个子系统包含的次级源和误差传感器数均为N，使用多通道FxLMS 算法。显然当I=1 时，集群式系统等效为集中式系统，当N=1 时等效为分散式系统。为了简化分析，假设每个误差传感器处的初级噪声均为由一个正弦信号经过初级通路模型产生的单频信号。所有子系统均使用该正弦信号作为参考输入，如式(1)所示，式中ω为信号的数字频率，n采样时间。

这样，整个系统的次级源和误差传感器总数均为NI，从第j个次级源到第k个误差传感器的次级通路传递函数在频率ω处的响应为

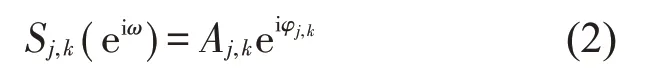
因此相应的滤波x信号为

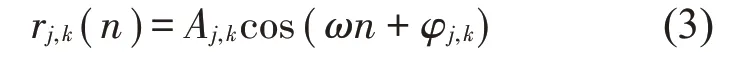
假设所有的子系统有相同的控制滤波器长度L与迭代系数μ，并在同一时刻开始控制，则误差信号和控制器系数迭代公式分别为

式中：e(n)为各个误差传感器接收到的误差信号矢量，d(n)为各个误差传感器处的初级噪声信号矢量，R(n)和为如式(6)和式(7)所示的滤波x 信号矩阵。由于子系统之间在物理上的互相影响是实际存在的，因此R(n)是所有元素均不为0的方块矩阵；而子系统之间互相独立，每个子系统只有自身的次级通路和误差信号信息，在进行系数迭代时无法考虑其它子系统的影响，因此是对角方块矩阵。

式(6)和式(7)中的Rp,q(n)表示第p 个子系统的传感器到第q个子系统的次级源之间的次级通路脉冲响应，如式(8)所示。

式中：w(n)为自适应滤波器控制系数矢量，如式(10)到式(12)所示。

式(12)中：wj,l(n)表示与第j 个次级源相关的自适应滤波器的第l个系数。如果用w(p-1)N+j,l(n)来表示第p 个子系统中第j 个滤波器的第l 个系数，则式(5)中单个系数的迭代公式如式(13)所示。

1.2 等效传递函数

对式(4)等号两侧做Z变换，整理得式(14)，在此式中，上标H 表示厄米特共轭，S 为如式(15)所示的次级通路响应矩阵。

式(15)中：Sp,q表示第p个子系统的次级源到第q个子系统的误差传感器之间的次级通路响应矩阵，如式(16)所示。

对式(13)做Z 变换，并代入式(14)中的Wl(z)可得

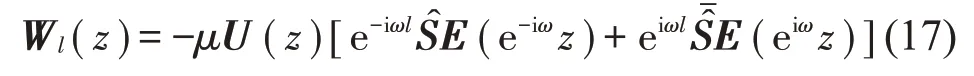
式中

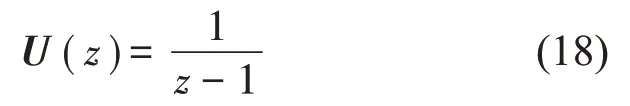
将式(17)代入式(14)，即可得到整个系统Z 变换后的方程，如式(20)所示。

式(20)中的求和部分包含的E(e±i2ωz)部分导致整个系统的传递函数无法直接得出。因此这里可以进一步假设参考信号为同步采样信号，且每L 个采样点对应参考信号整数个信号周期[9]。在这一前提下，Lω就等于π的整数倍，因此有

这样就去掉了式(21)中包含E(e±i2ωz)的部分，系统方程就化为

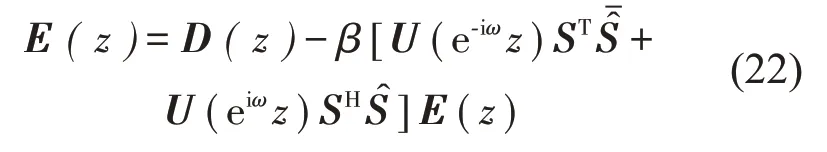
式中β称为归一化迭代系数，有

将式(18)代入式(22)，得到系统传递函数为

H(z)为NI×NI 传递函数矩阵，表示了每个误差传感器信号与所有初级噪声之间的关系。式(24)表示集群式系统的收敛过程等价于一个反馈系统，G(z)为开环传递函数矩阵，β为反馈增益。

2 算例

2.1 单个子系统

首先考虑单个子系统在自由空间中的情况，假设子系统本身为一个小型的集中式系统，有2 个次级源、2 个误差传感器，其空间位置如图2 所示。图中尺寸为与波数k 相关的归一化尺寸，即kd=1，即次级源和误差传感器分布在大小为1的正方形的四个顶角上。如果声速为344 m/s，对于频率100 Hz的信号，图中距离1实际表示约548 mm。

图2 集群式系统2通道子系统

自由空间中距离为l 的2 点之间的声耦合系数为

如果进一步假设扬声器和传感器电路的传递函数为1，则自由场中的次级通路响应矩阵为

此时传递函数矩阵H(z)为2×2矩阵，包含了4个传递函数。β 从0 变化到0.1 时，H(z)零点的变化轨迹如图3所示，根轨迹如图4所示，图中“○”表示β=0时的位置，“+”表示β=0.1时的位置。

注意到，在零点图中，随着β的变化有共轭零点始终保持在角度±ω处的单位圆上，说明H(e-iω)=0，也就是误差传感器处的信号为0，这与自适应系统的稳态性能一致。

图3 单个子系统的零点轨迹

在根轨迹图中，随着β的变化，极点从角度±ω处的单位圆上向圆内移动，根轨迹落在单位圆内。

说明当β=0时，极点与零点重合，H(e-iω)=1，也即误差传感器处的信号等于初级噪声，系统不起控制作用，对应μ=0时自适应系统不进行迭代。当β>0时，系统极点落在单位圆内，系统处于稳定状态。

图4 单个子系统的根轨迹

2.2 两个子系统

假设集群式系统包含2 个2.1 小节所述的子系统，子系统在自由空间中对称布置，子系统之间的距离为d1，如图5所示。

图5 对称布置的集群式系统

系统在不同d1下的稳定性如表1 所示，d1分别为-0.1、0、0.1和1时的误差迭代曲线如图6所示。

表1 集群式系统在d1不同时的稳定性

图6 d1不同时的收敛曲线

可以看到，当d1=-0.1时两个子系统的空间区域互相重叠，此时系统处于不稳定状态，这种情况下系统根轨迹如图7所示。

可以看到当β>0时，有根轨迹落在单位圆外，这解释了在这种情况下系统不稳定的原因。

图7 d1=-0.1时系统根轨迹分布

当d1=0时，系统处于临界稳定状态，此时系统传递函数H(z)在ω 处的响应如式(28)所示。可以看到式中矩阵每行有2个传递函数的幅度响应为0.5，这使得每个误差传感器的总响应均为1，即系统既不收敛，也不发散，处于临界稳定状态。

如图8 所示，在d1>0 时随着β 从0 改变到0.1，d1取值0.1和1时系统的根轨迹均落在单位圆内，因此此时系统均是稳定的，且图8(a)所示d1=0.1的根轨迹比图8(b)d1=1的根轨迹更靠近单位圆，这解释了d1=1时系统误差收敛的速度快于d1=0.1时的原因。

不同d1取值对收敛速度的影响如图9所示。结合图6 来看，随着d1从0 开始增加，系统误差的收敛速度不断增加，同时收敛速度的增加速度不断降低，当d1>0.5时，收敛速度的增加已经可以忽略了。

当d1很大时（如100），整个系统的零极点已经和第2.1小节的单个子系统保持一致，也就是说由于子系统之间距离很大，子系统之间的相互影响与自身次级源对误差传感器的影响相比已经可以忽略不计。

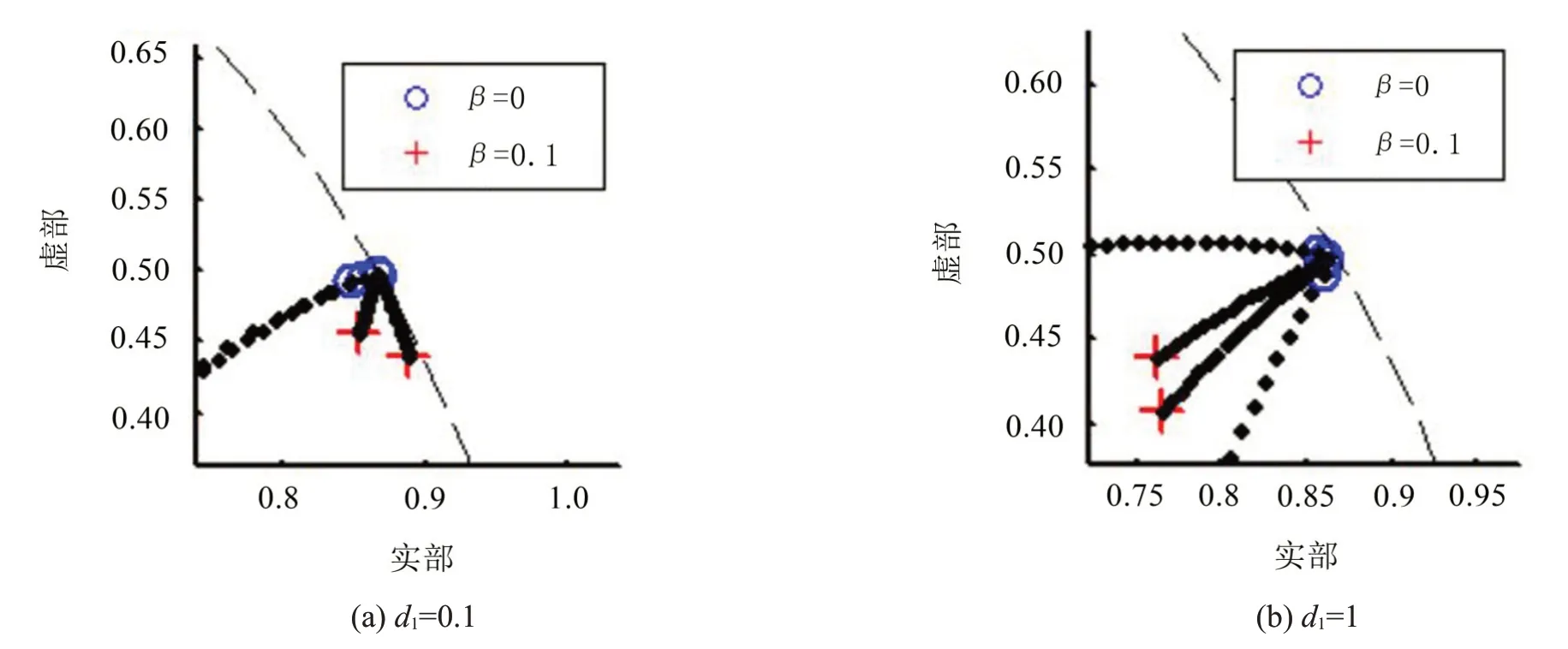
图8 d1>0时系统的根轨迹分布

图9 随着d1增大系统收敛曲线的变化

3 结语

本文对集群式有源噪声控制系统在控制单频噪声时的迭代公式进行Z 变换，推导得到等效传递函数。对系统等效传递函数的零极点图进行分析能预测系统稳定性和稳态误差，后续对单个子系统的仿真验证了理论推导的正确性。

考虑最简单的情况，假设集群式系统包含2 个对称放置的子系统。仿真结果表明，当2 个子系统的空间区域互相重叠，也就是距离小于0时，由于根轨迹分布在单位圆外，系统处于不稳定状态；当距离0时，系统处于临界稳定状态，此时等效传递函数中每个误差传感器的幅度响应为1，也就是说系统无效。如果要集群式系统有效，两个子系统之间的距离应至少大于0.5。因为如果距离小于0.5，此时系统虽然仍能保持稳定，但子系统之间的互相影响将强到导致误差收敛速度显著减慢，而相反地，如果距离大于0.5，子系统之间的互相影响就减弱到可以接受的程度，此时系统必定处于稳定状态，且有最佳的误差收敛速度。

由上述分析可以得出结论，集群式系统子系统的空间布放对系统稳定性有重要影响，子系统之间的互相影响越大，系统越接近不稳定状态，误差收敛速度越慢，反之亦然。总的来说，集群式系统的空间布放应满足以下两个原则：

(1)子系统的次级源和误差传感器应紧密布放，增大自身次级源对自身误差传感器的影响能力；

(2)尽可能减少子系统之间的互相影响，至少应使其至少小于子系统自身次级源对误差传感器的影响。