“车体-多边形化车轮-轨道”耦合系统动力分析及多边形车轮识别
雷晓燕,杨 天,刘庆杰
(华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌330013)
为满足社会发展的需要和人民日益增长的运输需求,现代铁路的运载量和运输速度不断提升,从而导致车轮与钢轨之间的关系变得复杂,轮轨磨耗严重。其中,车轮多边形化是车轮磨耗的主要形式,具体表现为沿车轮圆周方向上出现周期性磨损。车轮多边形化将严重影响轨道各部件和车体本身的稳定性,甚至会威胁到行车安全,为保障行车安全,排除运营过程中的安全隐患,列车车轮多边形问题亟待解决。
国内外研究人员对车轮多边形化的研究已经取得了一定成绩。B.Soua[1]等为研究车轮周期性磨耗问题,以数值仿真方法建立了车轮多边形化模型。仿真结果表明,轮轴扭转和车轮之间的横移会导致车轮多边形化,对车轮和轨道构成不利影响。我国学者王科[2]等为研究车轮多边形化的形成机理,建立了包含轨枕的“车轮-轨道”有限元仿真模型。仿真结果表明,轮轨系统的低频粘滑振动是导致车轮多边形磨损的主要因素,选择合适的扣件参数和轮轨之间的摩擦系数可以减少或者避免车轮多边形化的出现。
1 “车体-多边形化车轮-钢轨”耦合系统有限元模型
文中研究的车轮-轨道耦合属于状态非线性接触过程问题。当具有多边形形状的车轮在轨道上旋转时,车轮和轨道的接触状态改变,从而影响轨道状态和车轮与轨道的接触力。对于复杂的接触问题,ABAQUS有限元仿真软件有单独的分析模块,可以较好地处理非线性接触问题。利用ABAQUS 软件建立“车体-多边形化车轮-轨道”动力学仿真模型,为了提升计算效率,建模时取1/4车体、1/2转向架和单个车轮进行分析,轨道长度为15 m。选用基于Newmark 积分法的隐式动力分析模块进行求解,有限元模型如图1所示。

图1 有限元模型图
模型中列车车轮为实体模型,车轮半径为标准半径,通过编写ABAQUS可以直接读取的Python语言实现车轮多边形化,通过施加重力场代替直接作用力。模型中各部件参数选自CRH3型车体,如表1所示。

表1 车体模型参数表
文中重点研究“车体-多边形化车轮-轨道”耦合系统的垂向振动,使用“点对点”弹簧模拟列车一、二系悬挂,且只考虑垂向作用。在模型中,一、二系悬挂的连接点分别设置在车轮、转向架和车体的参考点处。悬挂系统参数如表2所示。

表2 悬挂系统参数表
在有限元计算中,计算结果的准确性受网格划分的影响。为了获得精确性更高的计算结果,特别是车轮与轨道之间的垂向作用力和钢轨应变,在有限元模型中用弹簧模拟扣件,其刚度为3×107N/m,阻尼为2.385×104N·s/m。模型中轨道结构包含钢轨和轨枕,为三维实体单元。钢轨和轨枕的参数如表3所示。
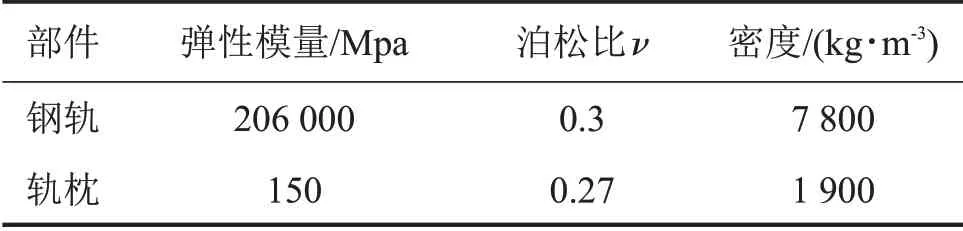
表3 模型参数表
在有限元计算中,计算结果的准确性受到网格划分的影响。为了获得精确性更高的计算结果,特别是车轮与轨道之间的垂向作用力和钢轨应变,模型各部分需要选取合适的单元类型及精确的网格尺寸,建立的模型中选取的单元类型为C3D8R,网格尺寸为20 mm。在进行有限元分析时,考虑了系统各部件的自重及载重。
2 仿真结果分析
输入模型参数,对“车体-多边形车轮-轨道”耦合系统进行动力学计算。仿真分析输出指标包括轮轨垂向接触力和钢轨垂向位移。

图2 轮轨垂向力及钢轨应变时程曲线
图2(a)为模型在有效运行时间内的轮轨垂向力时程曲线。从图中能够看到,具有多边形化的车轮在钢轨上转动时,轮轨垂向力随时间发生变化,在车速为200 km/h、波深为0.1 mm、在20 阶多边形条件下轮轨垂向力达到1.472×106N。按照剪力法的原理提取钢轨连续应变信号如图2(b)所示,从图中能够看到,多边形车轮转动过测点时,应变信号发生大小相等、方向相反的瞬时变化。
输入不同的模型参数,可分析得到不同车轮速度、多边形阶数和波深对轨道结构动力响应的影响。图3 为波深同为0.1 mm 时,不同车速和多边形阶数工况下轮轨垂向作用力的分布结果。从图3能够看出,1~5 阶多边形化车轮的轮轨垂向作用力随车速的改变不发生明显变化。6~20 阶多边形化车轮的轮轨垂向作用力随车速的升高不断变大,在相同速度条件下,当车轮多边形化阶数增加时,轮轨垂向作用力变大。

图3 波深为0.1 mm时车轮不圆对轮轨垂向力的影响
列车在实际运营时,列车车轮经常出现低阶多边形化。这种现象与低阶车轮失圆的形成机理密切相关,列车车轮在安装过程中如果发生偏心现象,在后续运行时车轮就会形成1 阶多边形化,三爪卡盘定位不准确则会使车轮形成3阶多边形化。为进一步分析低阶车轮不圆的影响,将输入参数固定为波深为0.1 mm,车速为200 km/h,提取1~5 阶多边形化车轮的垂向作用力和钢轨位移进行对比,结果如表4所示。

表4 不同阶数下轮轨垂向力及钢轨位移
从表4可以看出,对于低阶车轮多边形,在相同的速度和波深工况下,车轮多边形阶数为2阶时,轮轨间垂向作用力达到峰值126.8 kN,同时钢轨位移达到峰值0.884 4 mm。可以看出,低阶车轮多边形与高阶车轮多边形对轮轨垂向力的影响规律不同,不随不圆顺阶数的增大而增大。为了深入研究1~5阶车轮不圆作用下钢轨垂向力的变化,选取车速分别是200 km/h、250 km/h、300 km/h和350 km/h时的轮轨垂向力进行比较,如图4所示。

图4 低阶车轮不圆对轮轨垂向作用力的影响
为研究低阶多边形化车轮对轮轨垂向力和钢轨位移的影响,以3阶车轮多边形、200 km/h的速度工况为例,分别分析波深为0.1 mm、0.2 mm、0.3 mm、0.4 mm、0.5 mm 时5 种车轮多边形对轨道结构动力响应的影响。不同波深下轮轨垂向力和钢轨位移如表5所示。
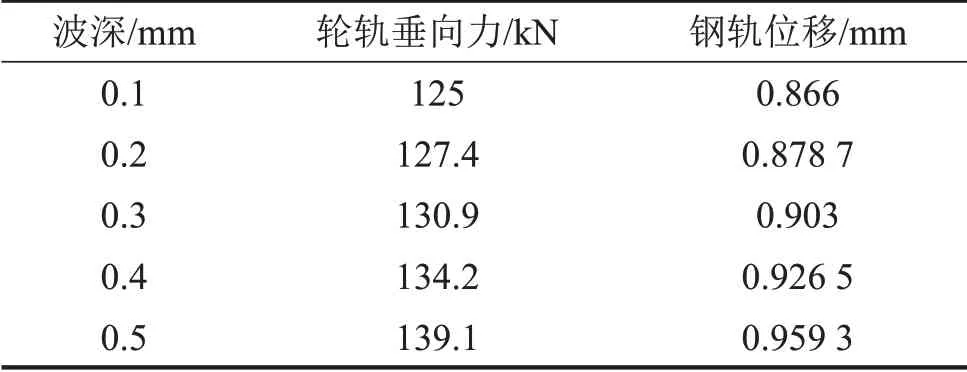
表5 3阶车轮多边形在不同波深工况下轮轨垂向力及钢轨位移
从表5 中能够看到,当车轮多边形化波深增大时,其引起的轮轨垂向力和钢轨位移随之增大。其中轮轨垂向作用力最大变化值为14.1 kN,钢轨位移最大变化值为0.093 3 mm,由此可见,波深对低阶车轮多边形引起的轮轨垂向力及钢轨位移无显著影响。为研究高阶多边形化车轮对轮轨垂向力和钢轨位移的影响,以11 阶车轮多边形、200 km/h 的速度工况为例进行分析,结果如表6所示。
从表6 能够看到,高阶车轮多边形引起的轮轨垂向力和钢轨位移同样随波深的增大而增大。其中轮轨垂向作用力最大变化值为56.9 kN,钢轨位移最大变化值为0.381 3 mm,通过对比可得,相对于低阶车轮多边形化,波深对高阶车轮多边形引起的轮轨垂向力及钢轨位移影响更为明显。
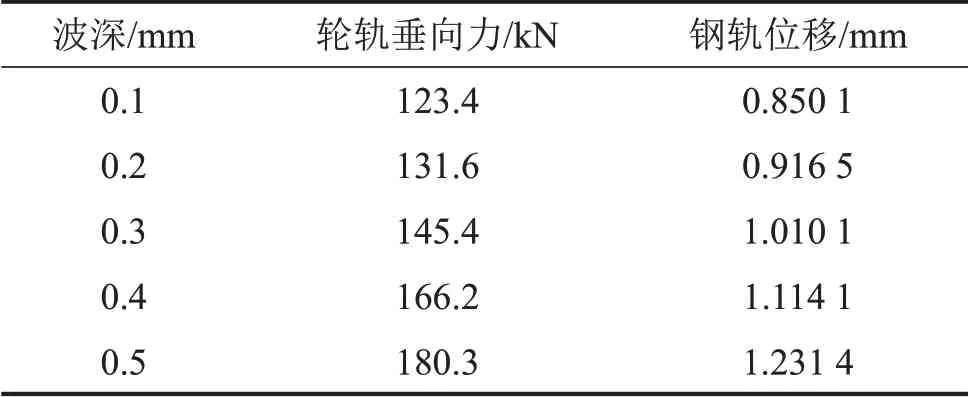
表6 11阶车轮多边形在不同波深工况下轮轨垂向力和位移
3 现场试验
为了验证动力学仿真模型的正确性,选择在某轨道试验中心进行现场测试。现场试验线路为直线段无砟轨道,采用60 kg/m 钢轨、混凝土III 型枕,轨枕间距为600 mm。主要试验装置有:动力牵引机车、配重转向架、电阻应变片等。试验现场如图5所示。

图5 试验现场图
现场试验中,应用剪力法测试轮轨垂向力,在距离跨中200 mm的两侧轨腰中和轴处粘贴应变片,应变片与钢轨中和轴纵向呈45°。贴片位置如图6所示。

图6 贴片位置图

图7 钢轨应变信号
启动试验设备,牵引机车匀速通过测试区间,采集到如图7(a)所示的应变信号。因为牵引车共有4个导向轮和4 个正常车轮,所以采集到的应变信号有多个波峰。提取采集结果,提取对象为单个转向架车轮,转向架车轮单通道应变信号如图7(b)所示。
由图7可以看出当车轮经过测点时应变方向发生改变,应变信号具有对称性,对比动力学仿真模型中钢轨应变信号,发现两种应变信号具有相同变化规律和趋势,验证了仿真模型的正确性。
提取实测得到的信号,通过数据拟合得到与实测应变信号相似的锯齿波函数,该函数有利于静力标定及车轮多边形识别。拟合锯齿波函数与原始数据对比如图8所示。
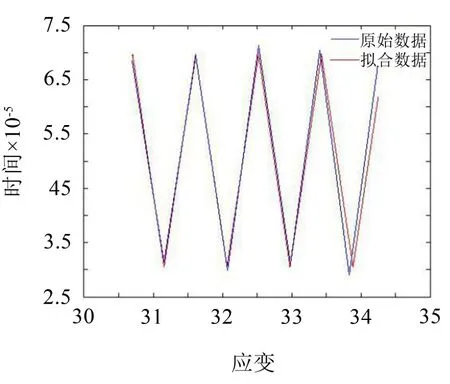
图8 拟合函数对比图
由图8可知拟合的锯齿波函数与实测结果具有很高的相似度。
图9为不同车速工况下轮轨垂向作用力连续应变信号。从图中能够看到,正常车轮在轨道上运行时,钢轨应变信号规律相同。由此可见,该锯齿波函数适用于不同车速工况下的轮轨垂向力标定,且不受车速影响。
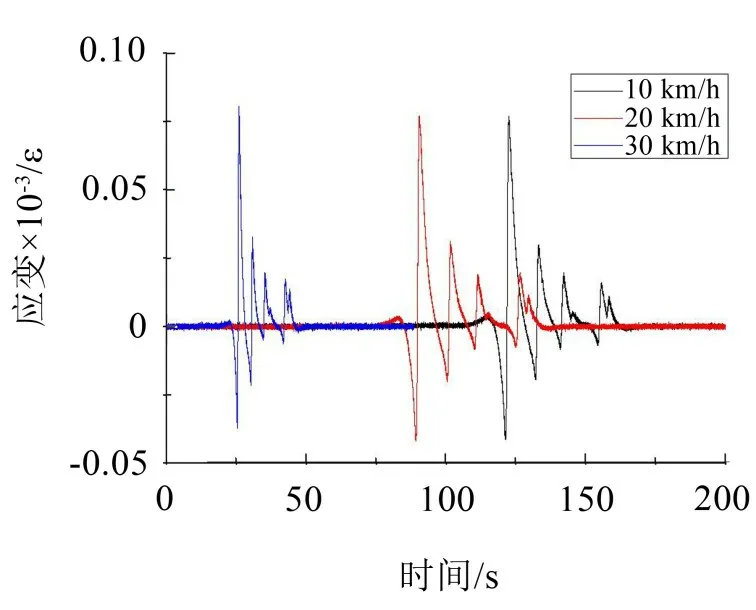
图9 不同车速工况下钢轨应变信号
4 车轮多边形识别
为验证拟合锯齿波函数的正确性,在模型中提取连续5 跨钢轨应变信号,通过锯齿波函数进行轮轨垂向力反演。将原始数据与反演出的轮轨垂向力数据进行对比,如图10所示。

图10 反演轮轨力与原始轮轨力对比
比较图10中两条数据曲线可以看出,有效时间历程为0.05 s,即车轮完整滚动一周时间内,原始数据曲线和反演数据曲线变化特征相同,且基本在同一时间点达到峰值。由于现场试验和仿真模型中的标定系数不同,所以两组数据在数值上存在差异,这并不影响通过拟合锯齿波函数来反演多边形化车轮引起的轮轨垂向作用力。
为证明锯齿波函数可以识别车轮多边形,以3阶车轮多边形为例,将其引起的钢轨连续应变信号通过锯齿波函数进行轮轨力反演,如图11(a)所示。在时域响应中,在车轮转动一圈时间内,轮轨垂向作用力3次达到峰值,表明3阶多边形化车轮对钢轨造成3 次冲击作用。图11(b)是轮轨垂向作用力在频域中的显示结果,从图中可以看出,3阶车轮多边形的转动频率为17.5 Hz。模型中车轮半径为标准车轮半径,车速为200 km/h,可以计算得到正常车轮的转动频率为5.3 Hz,因为车轮多边形具有周期性,所以3阶多边形化车轮的转动频率为15.9 Hz。由此可见,由锯齿波函数识别得到的车轮转动频率与理论频率相符。

图11 3阶车轮多边形识别结果

图12 11阶车轮多边形识别结果
继续用该锯齿波函数对11 阶多边形车轮进行识别,多边形化车轮其余参数不变。识别结果如图12所示。在时域响应中,11阶车轮多边形在有效时间历程内,轮轨垂向作用力变化频率大,与第3小节中11 阶多边形化车轮引起的轮轨垂向作用力变化规律相同。由图12(b)可以看出,车轮转动频率为59.4 Hz,符合11 阶多边形化车轮的理论转动频率58 Hz。此外,在频域响应内还包括26 Hz和38.1 Hz两种转动频率,与5 阶、7 阶多边形化车轮的转动频率相符。
通过上述识别过程和结果,能够验证基于轮轨垂向力连续测试识别车轮多边形方法的正确性,且该方法具有较高的准确度,可以明显反映出车轮多边形的特性。
5 结语
通过建立动力学有限元仿真模型和现场实测分析了车轮多边形所引起的轨道结构响应规律,并对车轮多边形进行识别,得到以下主要结论:
(1)建立了“车体-多边形化车轮-钢轨”耦合系统动力学有限元模型,得到轮轨垂向力和钢轨应变时域曲线。
(2)通过现场试验验证了有限元仿真模型的正确性,并通过试验数据拟合得到可以识别轮轨垂向力的锯齿波函数。
(3)总结了车轮多边形化对其所引起的轮轨垂向力和钢轨位移变化规律:低阶车轮多边形所引起的轮轨垂向力和钢轨位移受参数影响不敏感,且不存在明显规律性;随着参数的变化,高阶车轮多边形所引起的响应较低阶车轮多边形有明显改变,具有规律性,轮轨垂向力和钢轨位移随着3 个参数的增大而增大。
(4)通过轮轨垂向力反演验证了锯齿波函数的正确性,并通过锯齿波函数有效地识别出低速运行时车轮多边形特征。

