基于分数低阶统计量的频谱分析方法

李 辉

（天津职业技术师范大学机械工程学院，天津 300222）

在通信、医学及工程等领域的信号处理中，基于高斯分布的噪声模型具有广泛的理论基础，并得到了广泛的应用，但在许多实际应用中，由于受自然因素（如雷电、大气噪声等）和人为因素（如发动机、齿轮箱、电动机等故障）的影响，噪声表现出很强的脉冲冲击特性——非高斯特性，高斯分布不能很好地刻画此类噪声的特性，因而基于高斯分布模型假设的信号处理方法不能有效处理非高斯脉冲冲击信号，导致处理性能衰退，甚至完全失效。为了有效处理非高斯脉冲冲击信号，许多学者开展了广泛的研究，提出了混合高斯分布、柯西分布、t 分布和alpha 稳定分布等方法，以有效刻画非高斯脉冲冲击信号，其中，alpha 稳定分布不但满足广义中心极限定理，具有稳定性，而且与工程领域的许多实际数据相吻合，因而得到了广泛的应用。在数学领域，alpha 稳定分布的概念是Levy 于1925年在研究广义中心极限定理时提出的，20世纪80年代，alpha 稳定分布理论在数学领域得到了广泛的重视和发展[1]。但是，直到20世纪90年代，美国学者Nikias 及其研究团队才将alpha 稳定分布理论推广到信号处理领域，并系统建立了基于分数低阶统计量的信号处理框架，推动了该理论的发展和应用[2-7]。针对alpha 稳定分布噪声模型，国内外学者提出了许多理论和方法，其中，分数低阶统计量方法在通信信号处理[8-11]、工程信号处理[12-15]等领域得到了广泛的关注和应用。本文针对alpha 稳定分布噪声模型，提出了基于分数低阶统计量的频谱分析方法，对几种分数低阶统计量的频谱分析结果进行了对比，并用仿真信号验证了所提方法的正确性和有效性。

1 alpha稳定分布

1.1 alpha稳定分布定义

alpha 稳定分布常用来刻画具有脉冲冲击特性的信号和噪声的概率分布模型，但alpha 稳定分布没有显式的概率密度公式，只能用特征函数对其进行描述[3]。

如果随机变量x 的特征函数满足式（1），则称随机变量 x 服从 alpha 稳定分布，记为 x～s（α，β，γ，μ），且alpha 稳定分布由 α、β、γ 和μ等4个参数唯一确定。

式中：

式（1）中，α、β、γ 和 μ 的含义为：

（1）α 是特征指数（characteristic exponent），满足0＜α≤2。α 是描述alpha 稳定分布脉冲特性强弱的参数，α 越小，alpha 稳定分布的脉冲特性越强，概率密度函数 PDF 图的拖尾厚度越厚；反之，α 越大，alpha 稳定分布的脉冲特性越弱，概率密度函数图的拖尾厚度越薄，当α 参数不同时alpha 稳定分布的概率密度函数PDF 如图1所示。

（2）β 是偏度参数（skewness parameter），满足-1≤β≤1，是描述 alpha 稳定分布偏度的参数，当 β＜0 时，alpha 稳定分布的概率密度函数曲线向右倾斜；当β ＞0 时，alpha 稳定分布的概率密度函数曲线向左倾斜；当β=0 时，alpha 稳定分布的概率密度函数曲线对称，成为对称的alpha 稳定分布（symmetric alpha stable distribution，SαS），β 参数不同时 alpha 稳定分布的概率密度函数如图2所示。

图1 α 参数不同时alpha 稳定分布的概率密度函数

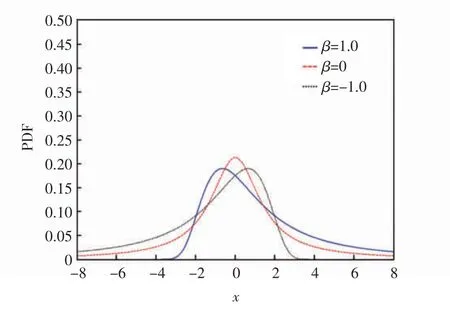
图2 β 参数不同时alpha 稳定分布的概率密度函数

（3）γ 是分散参数（dispersion parameter），满足γ≥0，其含义与高斯分布中的方差σ 相似，描述脉冲的离散程度，γ 参数不同时alpha 稳定分布的概率密度函数如图3所示。

图3 γ 参数不同时alpha 稳定分布的概率密度函数

（4）μ 是位置参数（location parameter），满足-∞＜μ＜∞，对于对称的 alpha 稳定分布，当 0＜α＜1时，μ 为中值；当 1＜α≤2 时，μ 为平均值，μ 参数不同时alpha 稳定分布的概率密度函数如图4所示。

alpha 稳定分布的特征函数φ（t）与其概率密度函数PDF 是傅里叶变换对，因此可以通过计算特征函数φ（t）的傅里叶变换，得到alpha 稳定分布的概率密度函数PDF。

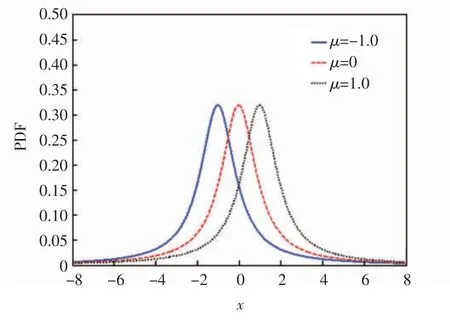
图4 μ 参数不同时alpha 稳定分布的概率密度函数

1.2 alpha稳定分布的主要性质

特征函数φ（t）是分析alpha 稳定分布的主要工具，利用式（1）可以推导出alpha 稳定分布的主要性质，并可得到对α、β、γ 和μ 4 个参数的解释。

性质1若x1和x2为独立的随机变量，且满足xi～s（αi，βi，γi，μi），i=1，2，则x=x1+x2满足x～s（α，β，γ，μ），且

性质2若 x～s（α，β，γ，μ），c 为实常数，则 x +c～ s（α，β，γ，μ +c）。

性质3若 x～s（α，β，γ，μ），当 0＜α＜2 时，对任意实常数 0＜p＜α，存在 E[|x|p]＜∞；对任意实常数 p≥α，存在E[|x|p]=∞。

性质4若 x～s（α，β，γ，μ），当 α=2 时，对任意实常数 p≥0，存在 E[|x|p]＜∞。

性质5当且仅当偏度参数 β=0 时，x～s（α，β，γ，μ）是关于 μ 对称的。

由性质3 和性质4 可知：

（1）当0＜α≤1时，alpha 稳定分布只存在分数低阶矩（p＜α），不存在一阶矩、二阶矩和高阶矩。

（2）当1＜α＜2时，alpha 稳定分布存在分数低阶矩（p＜α）和一阶矩，不存在二阶矩和高阶矩。

（3）当α=2时，alpha 稳定分布存在分数低阶矩（p＜α）、一阶矩、二阶矩和高阶矩。

2 分数低阶统计量

根据alpha 稳定分布的性质，对于服从alpha 稳定分布的随机变量 x，当 0＜α＜2 时，随机变量 x 的二阶及二阶以上的高阶统计量都是不存在的，因此基于二阶统计量的传统信号处理方法（如功率谱），在处理服从alpha 稳定分布的信号时，将导致性能衰退，甚至失效，而基于分数低阶统计量的信号处理方法是分析alpha 稳定分布信号的有效工具之一。分数低阶统计量主要包括分数低阶矩、共变、分数低阶相关、分数低阶协方差、相位分数低阶矩和相位分数低阶协方差。

2.1 分数低阶矩

若随机变量x～SαS，且满足 0＜α≤2，则其分数低阶矩（fractional lower order moment，FLOM）E[|x|p]定义为：

式中：Γ（·）为伽马函数，即：

2.2 共变

若随机变量x 和y 服从联合对称SαS 分布，且满足 1＜α≤2，则随机变量x 和 y 的共变为：

式中：γy为随机变量y 的分散参数，若y 为实数，则y＜p＞=|y|psign（y），若 y 为复数，则 y＜p＞=|y|p-1y*，（·）*为共轭运算符。

2.3 分数低阶相关

若随机变量x 和y 服从联合对称SαS 分布，且满足1＜α≤2，则随机变量 x 和 y 的分数低阶相关（fractional lower order correlation，FLOC）为：

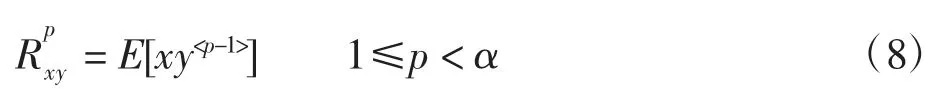
从式（8）可知：当p=2 时，分数低阶相关变为传统的自相关函数。

2.4 分数低阶协方差

若随机变量x 和y 服从联合对称SαS 分布，且满足0＜α≤2，则随机变量x 和y 的分数低阶协方差（fractional lower order covariance，FLOC）为：

2.5 相位分数低阶矩

若随机变量 x～SαS，且满足 0＜α≤2，则随机变量x的相位分数低阶矩（phased fractional lower order moment，PFLOM）为：

2.6 相位分数低阶协方差

若随机变量x 和y 服从联合对称SαS 分布，且满足0＜α≤2，则随机变量x 和y 的相位分数低阶协方差（phased fractional lower order covariance，PFLOC）为：

3 基于分数低阶统计量的频谱分析方法

根据传统的信号分析理论，若信号x 服从高斯分布规律，则其自相关函数Rx（τ）及功率谱Sx（f）为傅里叶变换对，即：

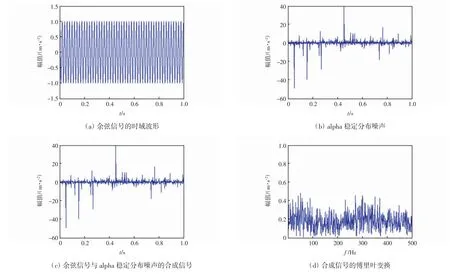
图5 余弦信号与alpha 稳定分布噪声的合成信号及其频谱

当信号x 不服从高斯分布规律，如服从alpha稳定分布时，由于信号x 的二阶统计量不存在，因而不能用传统的功率谱对其进行频谱分析。从前面分析可知：分数低阶统计量是处理alpha 稳定分布信号和噪声的有力工具，因此基于分数低阶统计量的频谱分析步骤为：

（1）计算信号x（t）的分数低阶统计量。

（2）计算信号x（t）分数低阶统计量的傅里叶变换。

为了验证该方法的正确性和有效性，假设信号x（t）为：

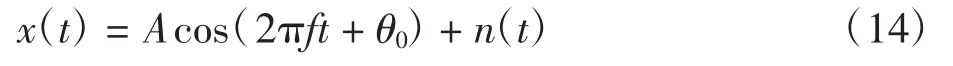
式中：A 为余弦信号的幅值；θ0为初始相位；n（t）为alpha稳定分布噪声。取A=1，θ0=0，f=50 Hz，采样频率fs=1 000 Hz，采样时间 1 s。

余弦信号与alpha 稳定分布噪声的合成信号及其频谱如图5所示。

合成信号的广义信噪比为GSNR=-5，从图5（c）很难看出合成信号中的周期性信号成分。从图5（d）中也难以识别频率为50 Hz 的周期成分。合成信号的自相关函数及其频谱如图6所示。由于alpha 稳定分布噪声的二阶统计量不存在，从图6（a）中看不出周期性的变化波形，而从图6（b）中也难以有效识别频率为50 Hz 的周期成分。因此，验证了基于二阶统计量的信号分析方法，在处理alpha 稳定分布信号时造成性能衰退或失效，因而传统的信号处理方法难以有效提取alpha 稳定分布噪声中的周期信号成分。

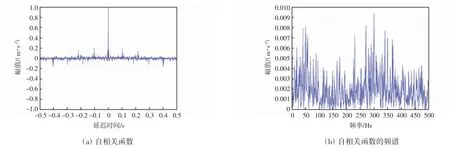
图6 合成信号的自相关函数及其频谱

为有效识别合成信号中的频谱成分，按本文提出的方法，先计算合成信号x（t）的分数低阶统计量，合成信号x（t）的共变、分数低阶相关、分数低阶协方差、相位分数低阶协方差，合成信号的分数低阶统计量如图7所示。

对比图6和图7可以看出，由于合成信号不存在二阶统计量，因此传统的自相关分析难以提取合成信号中的周期成分，而分数低阶统计量能从alpha 稳定分布噪声下，提取合成信号中的周期成分。同时，从图7还可以看出，分数低阶协方差和相位分数低阶协方差比共变或分数低阶相关的降噪性能更好，图7（c）和图7（d）比图7（a）和图7（b）中的周期性信号成分更明显。

合成信号的分数低阶统计量的傅里叶变换如图8所示。从图8可以看出，在频率50 Hz 处存在明显的峰值，因此基于分数低阶统计量的频谱分析方法能从alpha 稳定分布噪声下，有效提取频率为50 Hz 的成分。对比图8（c）、图8（d）和图8（a）、图8（b）可以看出，基于分数低阶协方差和相位分数低阶协方差的傅里叶变换比基于共变和分数低阶相关的傅里叶变换的降噪性能更好，因而基于分数低阶协方差和相位分数低阶协方差的频谱分析方法能更好地从alpha 稳定分布噪声下提取噪声信号中的频率成分。

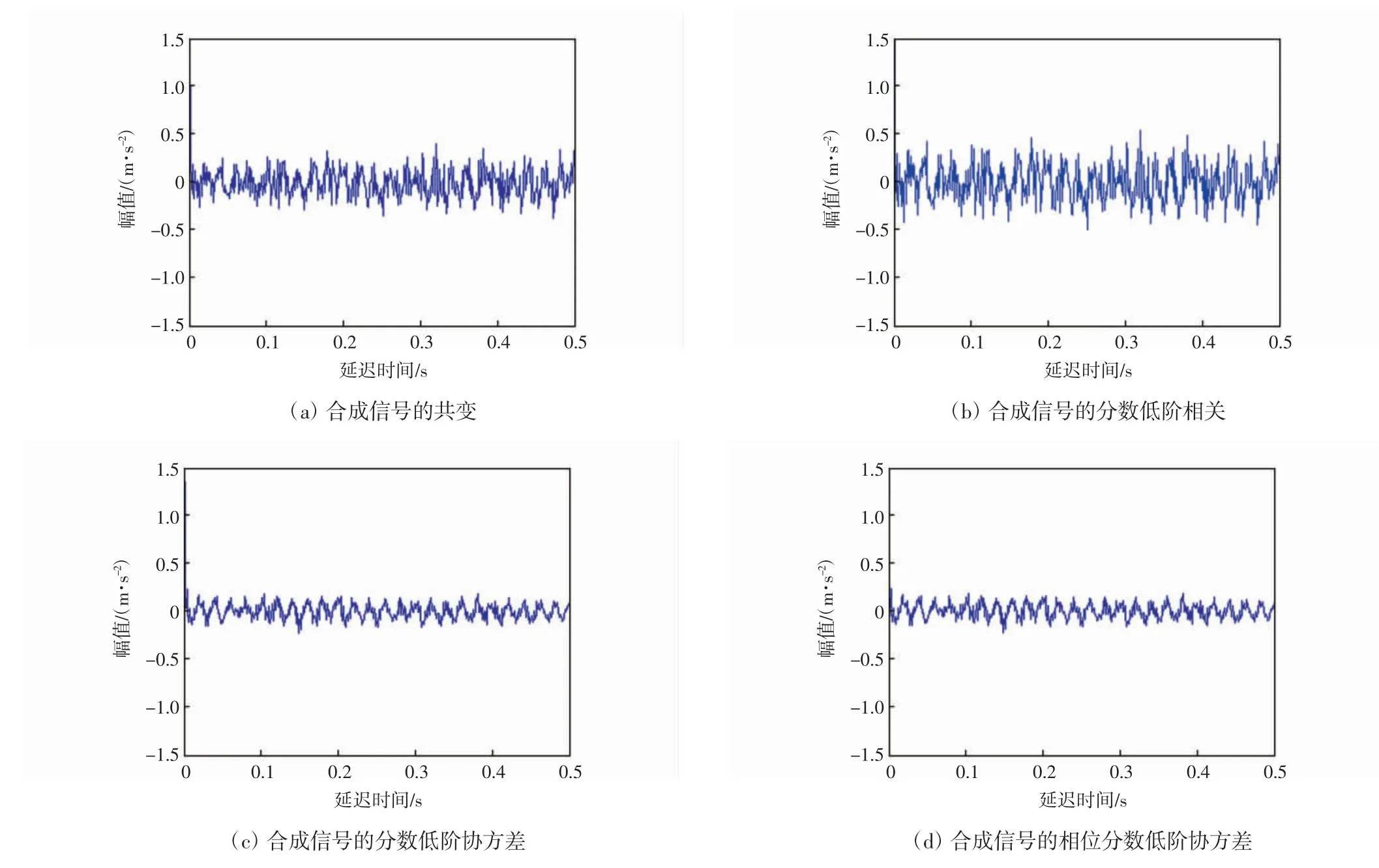
图7 合成信号的分数低阶统计量

图8 合成信号的分数低阶统计量的傅里叶变换

4 结 语

由于alpha 稳定分布信号的二阶统计量不存在，因而基于二阶统计量的传统频谱分析方法，难以有效处理alpha 稳定分布信号，而基于分数低阶统计量的信号分析方法是处理alpha 稳定分布信号的有力工具，基于分数低阶统计量的信号分析方法，能有效识别alpha 稳定分布噪声下的周期性频率成分。本文通过理论分析和仿真信号，验证了基于分数低阶协方差和相位分数低阶协方差的频谱分析方法具有更好的alpha 稳定分布噪声抑制能力，能更好地从alpha 稳定分布噪声下提取噪声信号中的频率成分，成为分析alpha 稳定分布信号的有力工具。