2种非对称广义高斯分布模型的构造

汪太月，戴燕青

(1.湖北工业大学 理学院，湖北 武汉 430068;2.湖北理工学院 数理学院，湖北 黄石 435003)

在通常的信号分析与处理中，大多数信号被假定为高斯分布(即正态分布)[1].但是，在实际的信号处理问题中，很多随机过程都是服从广义高斯分布(Generalized Gaussian Distribution,GGD)的.GGD在高斯分布的基础上增加了自适应系数，是高斯分布的拓展形式，且二者都是严格对称的分布[2].以GGD为特例的非对称广义高斯分布(Asymmetric Generalized Gaussian Distribution,AGGD)突破了对称性的限制，在处理不对称数据样本时更为灵活.相对高斯分布而言，GGD和AGGD所研究的对象更为复杂，经常被用于图像/视频信号处理及统计分析之中，其形状参数常被作为图像的特征进行分类或回归.例如，在基于变换域的数字图像处理中，小波变换[3]的系数、离散余弦变换的交流系数[4]都可用GGD或AGGD来拟合.在盲源分离及独立成分分析过程中[5]，将GGD或AGGD作为信号源的分布及评价函数也是合理的.此外，根据对实际观测数据的分析和研究，某些非高斯噪声[6]都可以采用它们来进行模拟.相比广义高斯分布而言，如同非对称高斯分布一样，非对称广义高斯分布突破了对称性的束缚.因此，在数据挖掘及信号处理的实际应用中，采用AGGD分析和建模更为合理，灵活性更强，适用范围也更为广泛.

1 非对称高斯分布模型

高斯分布是一种最常见的连续型随机分布，在概率论与数理统计的理论研究及实际应用中都占有非常重要的地位.在实际问题中，如果某个随机变量受到许多相互独立的随机因素影响，而每个随机因素都不能起决定性作用，那么就能断定该随机变量服从或近似服从高斯分布，如工件的测量误差；气象学中的温度及湿度；医学现象中同质群体身高、体重、红细胞数、血红蛋白量、胆固醇等.随着研究的深入，高斯分布在误差理论、产品检验、质量控制、质量管理、无线电噪声等领域中都有着广泛的应用[7].

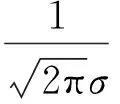
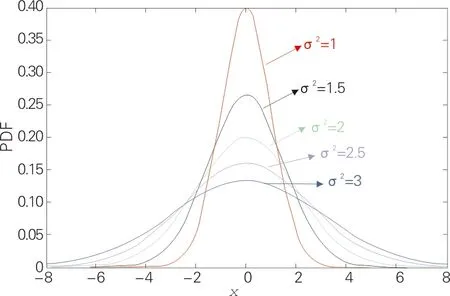
图1 高斯分布概率密度函数曲线(μ=0)

由图1可以看出，如果固定μ，改变σ2的值，则σ2愈小，曲线呈高而瘦；σ2愈大，曲线呈矮而胖.这说明高斯分布的概率密度函数的尺度由参数σ所决定，因此亦称σ为尺度参数.

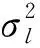
(1)

当式(1)中的Nl和Nr分别表示xk<μ和xk≥μ的样本容量时，模型可表示为：

(2)

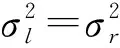
左右方差与偏斜程度之间有着密切的联系，偏度系数能用来量化非对称的概率密度函数的偏斜程度，即三阶参数为[8]：

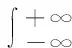
(3)

偏度系数能刻画数据分布的偏斜程度及方向，很好地反映分布偏离对称性的程度.若该系数为0，则表示数据分布严格对称；若呈右偏态(负偏态)分布，即右尾长，该系数就大于0；若呈左偏态(正偏态)分布，即左尾长，该系数就小于0.

2 广义高斯分布模型

源于广义Gamma分布的广义高斯分布是一种应用广泛的对称随机分布，可视为高斯分布的推广形式.Laplace分布是其特例，而连续型均匀分布和单位脉冲函数是其极限形式.广义Gamma分布的概率密度函数为[9]：

(4)

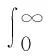
(5)

(6)

为简化计算，常常考虑μ=0的情形.

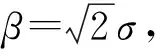
当α<2，为超高斯分布；α>2，为亚高斯分布[13].

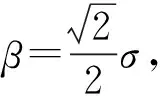
3) 当α→0时，有Kurtosis>3，此时GGD的概率密度函数趋于δ函数，即：

4) 当α→∞时，GGD趋于均匀分布.

μ=0，σ=10，α分别为2，1，0.7，100的概率密度函数曲线如图2所示.

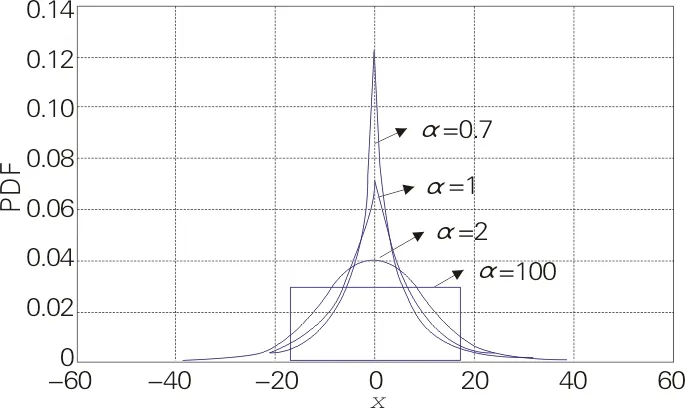
图2 不同参数α的GGD概率密度函数曲线(μ=0,σ=10)

3 非对称广义高斯分布模型的构造

3.1 左右两边的方差σ2不同产生的非对称

广义高斯分布族可用来描述可变尾长的对称分布.但对于非对称分布，就需要对GGD进行改进，构造出AGGD.前面我们用左右方差代替方差得到非对称高斯模型，于是，采用类似方法来建立AGGD模型，从而得到其概率密度函数表达式：

(7)

为研究分布的离散程度及峰值附近的陡峭程度，由式(7)所确定的非对称广义高斯分布随机变量的方差及其四阶矩分别为：

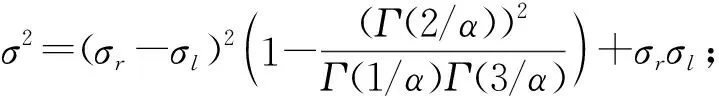
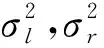
(a) α=0.7

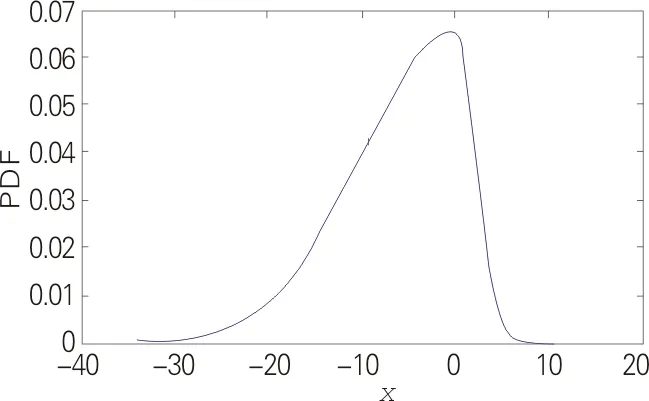
(b) α=2

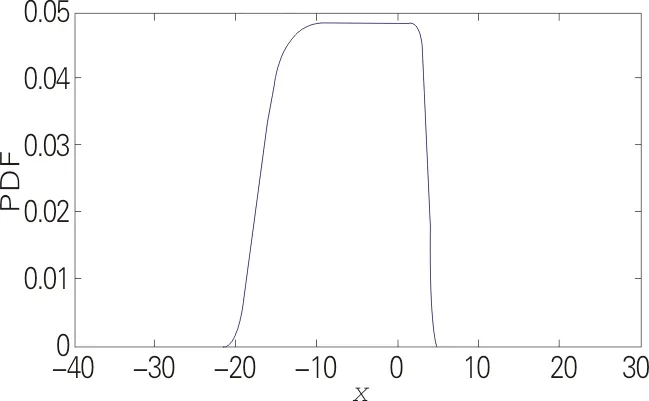
(c) α=10

(d) α=100

3.2 由2个不同密度函数产生的非对称

不失一般性，考虑μ=0的情形.令AGGD概率密度函数fagg的右半轴部分为GGD的概率密度函数fgg(x;αr,βr)的右侧，左半轴部分为GGD的概率密度函数fgg(x;αl,βl)的左侧，即：

(8)

fgg(0;αr,βr)=fgg(0;αl,βl).

即：

代入式(8)得：

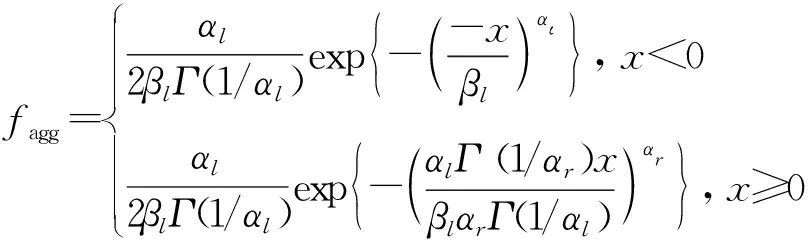
(9)

根据概率密度函数的正则性，有:

于是，可得到AGGD概率密度函数fagg的矩：

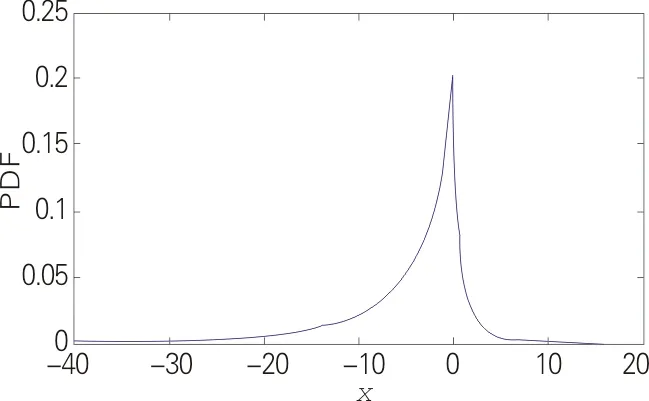
不同参数αl,αr的AGGD概率密度函数曲线如图4所示.由图4可知，若αl,αr中有一个参数不大于2，则概率密度函数曲线在μ=0处就不光滑，即μ=0是此模型构造的AGGD概率密度函数的奇异点.

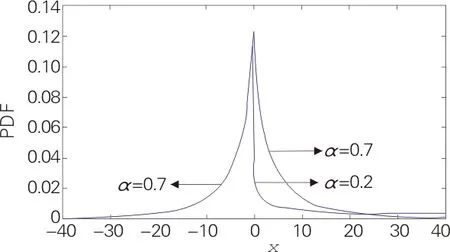
(αl=0.7,αr=0.2)

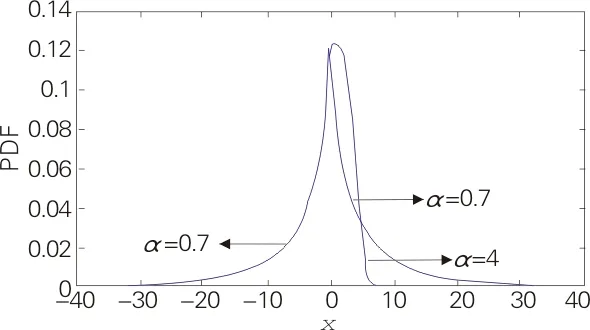
(αl=0.7,αr=4)

(αl=3,αr=1)

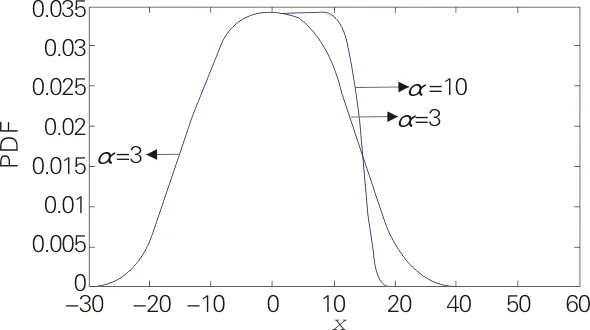
图4 不同参数αl,αr的AGGD概率密度函数曲线

4 结束语

非对称形式的广义高斯分布是一类较广义高斯分布更为复杂的分布形式，是广义高斯分布的延续和推广.利用GGD左右两边的方差不同及2个不同GGD概率密度函数在交接点处连续构造了AGGD模型，突破了高斯分布及广义高斯分布对称性的限制，减少了理论研究中的过多假设.在数据采集与处理、变换域图像分析、降噪去噪等应用领域，采用AGGD分析建模灵活性更强，适用性也更好.今后将进一步对其统计性质进行深入研究.