基于振速测量单全息面直接声场分离方法

田克权，毛 锦，李林聪，崔亚辉，杜进辅

(西安理工大学 机械与精密仪器工程学院，西安710048)

近场声全息是一种声源识别和声场可视化技术，通过测量声场的声压或振速信息，重建出三维声学特征，由于该方法在噪声源识别、定位时可以实现三维声场重现，有重要价值，引起了学术界的重视[1]，对于该技术目前研究最多的是基于空间变换（STFT）的近场声全息法，但其存在逆向重构不适定性问题，为了提高精度需要布置大量的传感器[2–3]。近年来对统计最优法[4–6]、边界元法[7–8]、等效源法近场声全息[9]研究也很多。

当存在相干声源时，需要把干扰声源分离后才能准确重建声场。毛锦等[10]通过改进统计最优声场分离法，采用双面测量在多个声源中分离出单个声源。张永斌等[11–12]基于声压振速联合声场数据，采用单测量面分离声源，将分离不对称声源的方法进行改进。J Hald[13]提出一种基于统计最优近场声全息法（SONAH），避免了傅里叶变换带来的卷绕误差，并采用正则化方法解决声学逆问题。Fernandezgrande E 等[14]提出一种基于双面振速声场分离速度的方法，并和直接速度重建声场方法、基于联合声压-振速测量的声场分离方法对比，证明这种算法在存在强烈干扰声时，也能有效分离声源速度。毕传兴等[15]提出非平稳多源声场分离模型，将时域插值法应用在声场分离方法中，为多声源声场分离技术研究奠定基础。毛锦等[16]利用测量数据存在误差的原理，采用单全息面实现了相干声源的分离。本文基于波叠加法近场声全息，采用单全息面推导声场分离模型，提出基于单全息面测量振速声场分离方法。通过仿真分析并和理论值对比，验证该方法的有效性。在声源频率不同时和基于单面声压声场分离方法对比，证明了本方法的优越性，所提方法对近场声全息应用推广具有积极意义。

1 理论研究

1.1 波叠加法近场声全息技术

波叠加法的基本原理：在振动体内部放置一系列等效简单源，以简单源产生声场叠加来替代振动体辐射声场。对于振动体V，表面边界S，根据波叠加基本原理有以下积分公式。

式中：p(r)是r处的声压，q(r0)是振动源源强，r0是等效源半径，ρ 是媒介的密度，ω 是声源振动角频率，g(r,r0)是在r处自由空间的格林函数。

式中：k是波数，k=ω/c，c是介质中声速。点r处振速可以用以下微分方程表示

式中：∇n是求法向梯度函数的运算符。

把声压和振速的求解公式简化表示为

式中：G、D 分别是等效源点和全息面之间的声压传递矩阵和法向振速传递矩阵，且G(r)=iρωg(r,r0)；D(r)=∇ng(r,r0)

对式（4）求逆运算，可得等效源源强

式中：G的上标“+”表示矩阵的广义逆。

根据式（4）可以求出等效简单源在自由空间场中任意位置R处的辐射声压

式中：pR是自由空间任意点R 处由等效源产生的声压，GR是等效源序列在空间R处的声压传递矩阵，Q称作声源源强。同样，可以根据质点振速求得声源源强并且得到自由空间任意点处质点振速。

1.2 基于单全息面测量振速声场分离

当全息面一侧存在相干声源干扰时，测量面上法向振速是两侧声源在全息面上法向振速的组合。声场分离的声场位置示意图如图1所示。

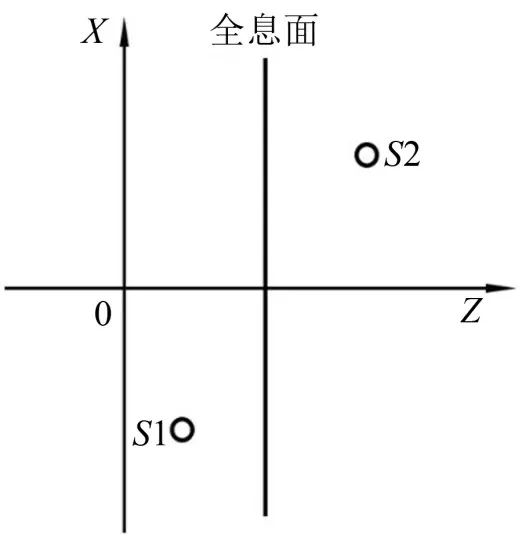
图1 声场位置示意图

由于测量数据存在误差，全息面H上法向振速v可以表示为

式中：v1b、v2b分别是声源S1、S2 在全息面H 上的理论振速,ε1、ε2分别是声源S1、S2 在全息面上振速测量误差。根据波叠加声场重构原理可得全息面上振速重构公式

式中：DH1、DH2分别是点声源S1和S2上的等效简单源与全息面测量点之间振速传递矩阵。因为ε1和ε2相对信号数值比较小，且采用正则化方法减小了误差对结果的影响，所以可以做以下近似表达

式（13）、式（14）分别代入式（11）、式（12）得

由式（10）转化得

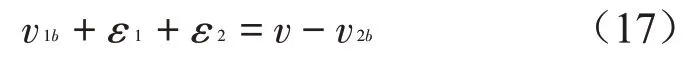
将式（16）代入式（17）得

根据式（10）中v2b+ε1+ε2=v-v1b，代入式（18）等式的右边可得

设v1≈v1b+ε1+ε2，可得v1近似表达式为

式中I表示单位矩阵。

式（20）即为基于单面测量振速分离振速的理论推导公式。质点振速得到后，质点声压可以利用波数域的Euler公式求得。

2 仿真分析

2.1 仿真1

以上推导了单面测量振速分离振速和声压的声场分离公式，为了验证本方法的正确性和优越性，分别用本方法和单面声压测量的声场分离方法分离全息面上法向质点振速和声压并进行比较。

仿真时，采用2 个半径为0.01 m、表面振速均为0.25 m/s、振动频率是1 200 Hz 的简单源，在直角坐标系下，两个声源位置分别是S1(-0.15，0，0) m、S2(0.15，0，0.3)m，全息面布置10×10的麦克风阵列，全息面Z轴方向的位置ZH=0.15 m，网格间距是0.07 m，在仿真数据中加入信噪比SNR=30 dB 的高斯白噪声。图2（a）和图2（b）是在全息面上的测量声压幅值和测量振速分布图，图3（a）和图3（b）分别是声源S1在全息面上产生的声压幅值和法向振速的理论分布。图4（a）和图4（b）分别是用本方法分离出的声源S1在测量面上产生的声压幅值和法向振速分布。图5（a）和图5（b）分别是用单面声压测量分离出的声压幅值和法向振速分布。

图2 2个声源共同在测量面上产生的声压幅值和法向振速

图3 声源1在全息面上产生的声压幅值和法向振速的理论分布

图4 基于单面测量振速分离出的声压幅值和法向振速

图5 基于单面声压测量分离出生的声压幅值和法向振速

从图2 至图5 中可以看出，由测量面直接测得2声源共同作用在全息面上的声压或振速不能准确反映声源1在测量面上的辐射信息。采用本文方法分离声场后，可以得到声源1 在全息面上的单独辐射信息，分离出的声压和理论声压、分离法向振速和理论法向振速都很吻合，单面声压测量分离法和本文方法分离结果有一定差异。为了定量分析分离精度，这里给出分离振速和分离声压的误差计算方法

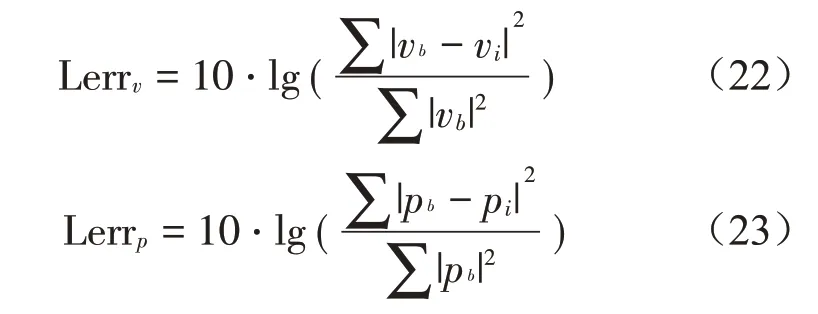
式中：vb是理论振速，vi是分离振速计算值。pb是理论声压，pi是分离声压计算值。

2种方法的仿真条件保持一致，单面测量声压分离声压（pp）和单面测量声压分离法向振速（pv）的相对误差级分别是-32.68 dB 和-30.61 dB；单面测量振速分离振速(vv)和单面测量振速分离声压(vp)的相对误差级分别是-33.45 dB和-28.34 dB。

在以上数值仿真基础上，进一步对比不同分离方法在不同频率下的分离误差，分析结果如图6所示。

从图6 中可以观察出2 种方法都可以有效分离声场，单面振速测量分离振速方法可以得到更高的振速分离精度，而单面声压测量分离声压法可以得到更高的声压分离精度。

2.2 仿真2

为了验证所提出的声场分离方法的适用性，进一步进行脉动声源仿真分析，2个脉动球源半径均为0.1 m，表面振速为0.25 m/s，声源和全息面位置如图7 所示，声源坐标分别是S1(-0.25，0，0)m、S2(0.25，0，0)m，采用仿真1 中的全息面测量阵列，全息面Z轴方向的位置ZH=0.25 m。

图6 不同频率下采用2种方法分离的声压和法向振速误差

对比2种分离方法分离不同频率脉动球源的误差，分析结果如图8所示。

从图8 中可以看出，对于分离脉动声源法向振速，由测量振速分离法向振速的精度比由测量声压分离振速的精度高。对于分离脉动声源声压，由测量声压分离声压的精度比由测量振速分离声压的精度高。

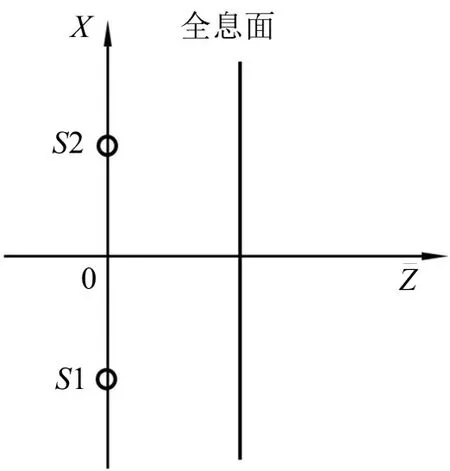
图7 声源位置和全息面位置

3 结语

本文以波叠加法为理论基础，建立单面振速测量声场分离模型，通过数值仿真验证了该方法的正确性，仿真1、仿真2 中通过和单面声压测量声场分离方法对比，发现单面振速测量的声场分离方法可以分离出更高精度的质点法向振速，在实际应用中可以采用单面测量振速声场分离方法，获取更精确振速分离结果。

图8 不同频率下采用2种方法分离脉动声压和法向振速误差