基于DOE及RSM的单线圈磁流变阻尼器优化设计及动力性能分析
胡国良,易锋,张佳伟,喻理梵
(华东交通大学 载运工具与装备教育部重点实验室,江西,南昌 330013)
磁流变液是一种新型智能流体,可在磁场作用下发生磁流变效应,即其流变性能在毫秒级的时间内随外部磁场强度变化而改变、且当外部磁场撤去时迅速转变成一般的牛顿液体[1-2]. 以磁流变液为核心介质的磁流变器件是极具市场前景的新型半主动控制元件,具有响应速度快、阻尼连续可调、可调范围宽等优点,并广泛应用于桥梁建筑、土木工程以及汽车行业的减振抗震领域[3-5].
磁流变阻尼器是以磁流变液为传动介质的一种典型减振器件. 其活塞杆端部设置励磁线圈,通过输入不同大小的电流,可实时控制输出阻尼力. 它具有输出阻尼力大、可调范围宽、适应性强、响应速度快及能量损耗低等特点[6]. 近年来国内外学者在磁流变阻尼器的结构设计方面做了系列研究[7-10]. 针对阻尼器液流通道,先后设计了内通道、外通道以及蛇形通道等结构;针对励磁线圈,先后设计了单线圈、双线圈以及多级线圈;另外,研究学者在功能集成化方向也有了进一步研究,研发了自感应式及自供电式磁流变阻尼器等.
为进一步提高磁流变阻尼器的动力性能,国内外研究学者在阻尼器结构优化设计方面也作了许多研究. 扎哈穆法汉工程技术学院的Khan等[11]提出了一种基于对比分析的优化方法,分别对端部平直、端部倒角以及端部圆角三种不同类型活塞头的磁流变阻尼器进行了阻尼力仿真分析,结果表明活塞头设置为端部圆角形状时可使提供更大输出阻尼力;但该优化仅仅针对不同类型的活塞头结构,并未涉及到精确尺寸的优化方法. 韩国仁川大学的Sung等[12]提出一种基于ANSYS软件的一阶优化方法,并对磁流变阻尼器进行优化设计,利用1/4车辆座椅悬架分别对初始和优化后的阻尼器进行实验测试,结果表明优化后的阻尼器在输出阻尼力及功耗等方面均有更好的性能,但该优化方法受限ANSYS软件,存在优化步骤繁琐、优化结果不完全一致等缺点. 萨卡利亚大学的Parlak等[13]提出一种基于DOE的优化设计方法,分别选择阻尼间隙宽度、法兰厚度、活塞芯半径以及输入电流4个参数作为设计变量,并利用L9正交表得到9种不同结构参数的阻尼器,以最大动态范围和最大输出阻尼力为目标函数寻找最优结构参数并进行动力性能实验测试,结果表明优化后的阻尼器可提供更大的阻尼力和更宽的动态范围. 相比传统的优化方法,基于DOE的优化方法可实现多目标的优化,但由于设置的水平值有限,故无法对结构尺寸进行精准的优化. 韩国材料与机械研究所的Moon等[14]提出了一种次优化程序,首先通过数值模拟确定要设计的阻尼器的阻尼力和速度,进而通过引入活塞直径、杆长以及间隙尺寸等约束构建非线性优化问题并设置最大动态范围为优化目标,最终运行优化程序得到最优的尺寸参数. 该优化方法可以对结构尺寸进行精准的多目标优化,但该方法仍然存在约束变量较少、优化方法单一等缺点.
以上各类优化设计方法可得到动力性能更优的磁流变阻尼器结构,但均存在一定的局限性,如步骤繁琐、优化效果不佳、优化方法单一等. 基于此,本文首先设计了一种单线圈磁流变阻尼器,并提出了一种基于DOE及RSM的优化方法对其进行结构优化设计. 该优化方法通过DOE找到设计参数范围内的设计组合进行有限元分析,并使用RSM进行多项式函数拟合,建立阻尼器性能与设计变量之间的模型,然后建立结合输出阻尼力和可调范围的多目标函数并利用SQP算法进行优化计算. 同时通过仿真及实验测试对优化前后的阻尼器进行动力性能分析.
1 单线圈磁流变阻尼器工作原理
1.1 工作原理
传统的汽车减振器是双筒液压减振器,属于被动控制器件,由于其阻尼力无法连续可调故减振效果较差. 基于此,设计了一种如图1所示的单线圈磁流变阻尼器,主要由吊耳、端盖、活塞杆、绕线架、阻尼器缸体、浮动活塞以及励磁线圈等构成. 以磁流变效应为机理的磁流变阻尼器可使输出阻尼力随外加电流可调,有效解决传统汽车液压减振器减振效果差的问题.
阻尼器缸体内充满磁流变液,绕线架和浮动活塞将阻尼器内腔分为拉伸腔、压缩腔和补偿腔三个部分. 阻尼器工作过程包括拉伸过程和压缩过程,活塞头从最大负行程位置运动到最大正行程位置即为拉伸过程,活塞头从最大正行程位置运动到最大负行程位置即为压缩行程. 活塞头往复运动过程中,磁流变液受到挤压在拉伸腔与压缩腔之间来回流动. 当励磁线圈通入电流时,有效阻尼间隙处将产生感应磁场,有效阻尼间隙处的磁流变液发生磁流变效应产生剪切应力,阻碍活塞头相对运动,从而使磁流变阻尼器产生输出阻尼力. 由于该磁流变阻尼器为单出杆式结构,拉伸腔与压缩腔的有效工作面积不等,因此设置浮动活塞构成补偿腔进行液体体积补偿.
1.2 数学模型
该阻尼器工作模式为剪切阀式,采用Bingham模型进行阻尼力数学模型推导,阻尼器输出阻尼力包括库伦阻尼力和黏滞阻尼力两部分[4]:
F=Fc+Fη,
(1)
式中:Fc为库伦阻尼力;Fη为黏滞阻尼力.
剪切阀式阻尼器的阻尼力可看作阀式阻尼力与剪切式阻尼力之和. 剪切式库伦阻尼力为
Fsc=2πdbtτy,
(2)
式中:t为有效阻尼间隙长度;db为活塞头的外径;τy为磁流变液的剪切应力.
阀式库伦阻尼力为
(3)
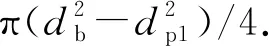
剪切式黏滞阻尼力为
Fsη=2πηdbtv/b,
(4)
式中v为活塞杆的运动速度.
阀式黏滞阻尼力为
(5)
将式(2)~(5)整合到式(1)中,得到:
[2πdbt+6tAp/bAp]τy.
(6)
剪切式阻尼力与阀式阻尼力在总阻尼力的占比可以分别通过剪切式与阀式库伦阻尼力的比值、剪切式与阀式黏滞阻尼力的比值来进行分析. 其中,库伦阻尼力的比值为
Kc=Fsc/Fvc=4b/(3db).
(7)
黏滞阻尼力的比值为
Kη=Fsη/Fvη=(4b/3db)2.
(8)
通常情况下,磁流变阻尼器的阻尼间隙宽度b取值较小,一般为1~2 mm,而活塞头直径db远大于阻尼间隙宽度b,所以剪切式阻尼力一般可忽略不计,该阻尼器的阻尼力公式可简化为
(9)
式中c为经验设计系数,取0.5.
阻尼器的输出阻尼力可调范围为
K=F/Fη.
(10)
2 基于DOE及RSM的单线圈磁流变阻尼器结构优化设计
2.1 响应面函数
响应曲面法(RSM)是一种以数量化分析输入与输出之间的数学关系,从而构建可反映输入输出关系的合理数学模型的方法. 实验设计(DOE)是一系列试验统计分析,通过有目的改变某系统的输入观察输出的变化情况. 利用RSM进行优化设计需要建立在DOE基础上,通过DOE找到设计参数范围内一些设计组合进行有限元分析,然后使用RSM进行多项式函数拟合,建立阻尼器性能与设计变量之间的模型,从而为优化设计建立基础[15].
RSM的响应面函数一般用多项式表示为
(11)
精确输出响应为
(12)

近似函数与设计变量之间的回归模型一般可用多项式函数表示为
(13)
回归分析的主要目的就是找到合适的待定系数β,从而尽可能地减小近似响应与精确响应之间的误差ε. 通过矩阵运算可反求待定系数β.
β=(XTX)-1XTy.
(14)
选用一次模型进行建模,该模型包括常数项、线性项以及相互作用项,是一种可以反映参数之间相互作用的模型. 该多项式函数可表示为
a12x1x2+a13x1x3+a14x1x4+a23x2x3+
a24x2x4+a34x3x4.
(15)
磁路部分是影响磁流变阻尼器动力性能的关键部分,优化主要针对于单线圈磁流变阻尼器的磁路部分进行,因此建立了如图2所示的优化模型简图. 优化目的是得到一定体积内性能最优的磁流变阻尼器结构,首先保证阻尼器缸体直径不变,即D=50 mm,活塞头的长度不变,即l=45 mm.
通过分析阻尼力数学模型可知,影响阻尼器输出阻尼力大小的关键参数包括:有效阻尼间隙t、绕线槽深度w、阻尼间隙宽度b及阻尼器缸体厚度dh. 因此选择这4个参数作为设计变量,同时每个参数设置3个水平数,具体数值如表1所示.

表1 设计变量及水平数
优化目标旨在最大化输出阻尼力及可调范围,两者均与磁流变液的剪切应力τy相关,影响剪切应力τy的主要参数为有效阻尼间隙处磁感应强度B. 本方法旨在得到各设计变量与阻尼间隙处磁感应强度B影响关系,所以定义通入电流I=1 A时有效阻尼间隙处的磁感应强度B作为DOE实验指标. 根据所选的设置变量及设置的水平数,得到立方实验设计表,其中每组有效阻尼间隙处的磁感应强度B通过FEM的方法得到.

B=a0+a1t+a2w+a3b+a4dh+
a12tw+a13tb+a14tdh+a23wb+
a24wdh+a34bdh.
(16)
结合由DOE方法得到的表2实验设计表中的参数组合及式(16),利用Matlab软件计算得到磁感应强度B与设计变量之间关系的响应面函数:
B=1.931 7-0.055 1t-0.039 0w-0.909 9b-
0.025 9dh+(9.375e-5)tw+0.031 8tb-
(7.159e-4)tdh+0.030 7wb-0.01wdh+
0.037 9bdh.
(17)
2.2 优化设计
为使阻尼器得到更大的输出阻尼力以及更宽的可调范围,建立了一个包含多个性能指标的多目标函数:
(18)
式中:FR与Fo为分别为优化前最大阻尼力和优化后最大阻尼力;Kr与Ko分别为优化前动态范围和优化后动态范围;aF与aK分别为阻尼力权重系数和可调范围权重系数,综合考虑汽车在不同路面行驶过程中的输出阻尼力和可调范围要求,aF与aK分别取0.5和0.5.
该优化设计在固定的外形尺寸参数下进行,通过分析各部分尺寸参数,确定优化约束空间如表2所示.

表2 设计变量约束空间
优化目的是为了得到更大的输出阻尼力及更宽的可调范围,因此优化目标可以看作为使目标函数最小化,优化设计问题可以表述如下,编写程序并利用Matlab软件工具箱中的SQP算法来进行非线性数学规划.
subject to 4≤t≤8;6≤w≤8.5;
0.5≤b≤1.5;4≤dh≤8.
(19)
图3所示为基于DOE及RSM的单线圈磁流变阻尼器优化设计参数迭代图,该优化过程一共经历了9次迭代. 由图3(a)可知各设计变量值均在经历初期较大变化后随迭代次数的增加而趋于平稳;另外,由图3(b)可知目标函数fOBJ在第9次迭代达到最小值,即得到最优结果. 优化前后设计变量的值如表3所示.

表3 优化前后设计变量值
3 单线圈磁流变阻尼器仿真分析
3.1 电磁场仿真
利用ANSYS分别对优化前后的阻尼器进行电磁场仿真分析,首先建立了如图4所示的阻尼器二维简化仿真模型. 由图4及表3可知,优化前后阻尼器的结构相同,仅对应的尺寸大小不同. 接着网格划分、电流加载及施加磁力线边界条件,最后通过求解及后处理得到如图5所示磁力线分布图. 观察图5可知,优化前后阻尼器磁力线均经过绕线架和阻尼器缸体行成闭合回路,并垂直通过有效阻尼间隙处. 另外,由于整个阻尼器缸体均为导磁材料,优化前后阻尼器均存在少量的漏磁现象.
通过仿真计算选取有效阻尼间隙处的平均磁感应强度作为该处的磁感应强度,得到了如图6所示磁感应强度随电流变化程度. 由图可知,仿真电流由0加载到1.5 A,励磁线圈产生的磁感应强度逐渐增大,优化前后阻尼器有效阻尼间隙处磁感应强度也逐渐增大. 优化前阻尼器在电流为1.0 A时逐渐趋于饱和,最大磁感应强度为0.48 T;优化后的阻尼器在电流为1.2 A时逐渐趋于饱和,最大磁感应强度为0.53 T.
3.2 动力性能仿真
为直观比较优化前后磁流变阻尼器的动力性能,仿真过程中,选取每个电流下的平稳峰值的平均值作为该电流下的阻尼力,得到如图7所示的优化前后的阻尼力随电流变化曲线. 由图可知,优化前后的阻尼力均随电流增加而增加;当电流为1.5 A时,优化后的阻尼力达1 500 N,而优化前的阻尼力仅有1 000 N. 优化后的阻尼力比优化前的阻尼力增加了500 N,初步说明优化后阻尼器具有更好的阻尼性能,优化设计达到了增加输出阻尼力的要求.
图8所示为优化前后动态范围仿真对比图. 由图可知,优化后最大可调范围可达44,而优化前最大可调范围仅有40. 优化后的动态范围得到了增加,表明优化设计达到了扩大阻尼力可调范围的目的.
4 单线圈磁流变阻尼器性能测试分析
4.1 动力特性测试系统
为进一步对仿真结果进行验证,分别加工了如图9和图10所示优化前后的磁流变阻尼器.
利用INSTRON疲劳拉伸机搭建了如图11所示磁流变阻尼器动力特性试验台. 试验台主要由直流稳压电源、疲劳拉伸机、磁流变阻尼器以及信息采集主机4部分组成. 电源为阻尼器提供电流激励;疲劳拉伸机产生不同类型正弦激励;阻尼器活塞杆装夹在疲劳拉伸机的动力杆上,底部端盖装夹在疲劳拉伸机的工作台上;疲劳拉伸机上安装有位移传感器和力传感器,信息采集主机与传感器相连接,实时记录阻尼器工作过程中力与位置信息.
4.2 优化前阻尼器动力性能
磁流变阻尼器在动力特性试验台上进行实验测试时,由于所加载的外部激励为正弦振动,活塞杆将带动活塞在阻尼器缸体内往复运动. 阻尼器活塞运动可以分为压缩和拉伸两个工作行程. 因此,测试得到的动力特性曲线将包含压缩阻尼力和拉伸阻尼力,曲线的上半部分为拉伸阻尼力,下半部分为压缩阻尼力. 图12所示为不同电流下优化前阻尼器的阻尼力-位移关系曲线. 由图可知,拉伸和压缩阻尼力均随电流的增加而增加,且变化趋势与仿真曲线基本一致. 其主要原因在于随着电流的增加,励磁线圈产生的感应磁场增加,从而导致阻尼器的库伦阻尼力增加,最终使输出阻尼力逐渐增大. 另外,随着电流的增加阻尼力的增大范围逐渐变小,并在I=1.25 A后趋近饱和,并在电流为1.50 A时达到最大值,拉伸阻尼力为140 N,压缩阻尼力为220 N.
与此同时,图12所示的阻尼力-位移曲线呈圆滑饱满的“回”字型,与理论曲线基本符合. 然而,拉伸阻尼力仍然存在一定程度的缺失,这大致的原因可能是灌注磁流变液时,阻尼器内部混有少量的空气,使得磁流变液灌注不充分.
图13所示为不同频率下优化前阻尼器的阻尼力-位移关系曲线. 由图可知,输出阻尼力随频率的增加也略微增加. 这是由于磁流变阻尼器在工作时,阻尼力包括库伦阻尼力和黏滞阻尼力,库伦阻尼力与磁场强度有关,电流保持不变时,库伦阻尼力也保持不变;黏滞阻尼力与活塞杆运动速度有关,所以频率的增大使活塞杆的运动速率增加,黏滞阻尼力也随之增加,但黏滞阻尼力占比较小,因此总输出阻尼力只是略微的增加.
图14所示为不同振幅下优化前阻尼器的阻尼力-位移关系曲线. 由图可知,随着振幅的增大,阻尼器的阻尼力略微增加. 这是因为频率一定时,振幅的增大会使活塞杆的运动速率增加,导致黏滞阻尼力增加,使总输出阻尼力略微增加.
为直观显示阻尼力与活塞杆振动速度的变化关系,对位移求导得到如图15所示的不同电流下优化前阻尼器的阻尼力-速度关系曲线. 由图可知,阻尼力随电流增加而增加;同时随速度的增加呈一定程度的倾斜,阻尼力随速度的增加而略微增加.
4.3 优化后阻尼器动力性能
图16所示为不同电流下优化后阻尼器的阻尼力-位移关系曲线. 由图可知,优化后阻尼器的阻尼力-位移关系曲线与优化前变化规律相同,拉伸和压缩阻尼力均随电流的增加而增加. 阻尼力-位移曲线呈饱满圆环的“回”字形,表明该优化后的磁流变阻尼器能较好的体现阻尼力做功特点. 另外,输出阻尼力随电流增加而增加,并在电流为1.50 A时趋近饱和,拉伸最大阻尼力达350 N,压缩最大阻尼力达430 N.
图17所示为不同频率下优化后阻尼器的阻尼力-位移关系曲线. 由于振幅保持不变时,频率增大将使活塞杆运动速度增大,因此阻尼力随频率增大而略微增大,该变化规律符合理论分析.
图18所示为不同振幅下优化后阻尼器的阻尼力-位移关系曲线. 由于频率保持不变时,振幅增大将使活塞杆运动速度增大,因此随着振幅的增大,阻尼器的输出阻尼力略微增加.
图19所示优化后阻尼器在不同电流下阻尼力-速度关系曲线. 由图可知,阻尼力随电流的增大而增大;同时,阻尼力随着速度的增加而增加.
4.4 优化前后阻尼力动力性能对比分析
图20所示为优化前后的阻尼器在电流为0, 0.5,1.0和1.5 A时动力特性对比图. 观察图像可知,外加电流在0~1.5 A时优化后的磁流变阻尼器阻尼力总是大于优化前的阻尼器,并且随着电流增加优化前后的阻尼力差值也逐渐增大,同时在优化前后阻尼器均达到饱和时保持稳定. 由此可知,优化后的阻尼器较优化前的具有更优的动力性能.
图21所示为频率0.75 Hz、振幅为12.5 mm的正弦激励下阻尼力随电流变化对比曲线. 由图可知,优化前后磁流变阻尼器的输出阻尼力均随电流增加而增加;另外,优化后阻尼器的输出阻尼力较优化前阻尼器明显增加. 当电流为0 A,振幅为12.5 mm时,优化后输出阻尼力为116 N,相较于优化前的输出阻尼力(68 N)增加了48 N. 在实际工程应用中,需要较大的初始阻尼力,故优化后的磁流变阻尼器更加适用于工程应用中. 当电流为1.5 A,振幅为12.5 mm时,优化后阻尼器的输出阻尼力可达560 N,优化前阻尼器的输出阻尼力仅有253 N;优化后阻尼器的最大输出阻尼力比优化前的阻尼器增加了约300 N,增益率达120%.
图22所示为优化前后磁流变阻尼器的可调范围对比图. 由图可知,优化前阻尼器的最大动态范围为3.7,而优化后阻尼器的最大动态范围为4.8,增益率达30%. 对比分析表明,对阻尼器进行结构优化设计使阻尼器阻尼力和动态范围均有显著增加,优化后的磁流变阻尼器在不改变外形尺寸的条件下具有更优的动力性能,验证了优化设计方法的准确性及有效性,拓宽了磁流变阻尼器的实际应用.
5 结 论
设计了一种单线圈磁流变阻尼器,并提出一种基于DOE及RSM的优化设计方法对其进行结构优化设计. 对优化前后阻尼器进行了仿真分析,并搭建试验台对优化前后阻尼器进行了动力性能测试,得出以下结论.
① 优化前后的磁流变阻尼器输出阻尼力均随电流增加而增加,阻尼力连续可调. 说明单线圈磁流变阻尼器可实现半主动控制,可作为汽车减振器提供良好的减振性能.
② 对磁流变阻尼器进行动力性能测试,当外加电流1.5 A时,测得优化前阻尼器输出最大阻尼力达220 N,优化后阻尼器输出阻尼力达430 N. 说明优化后阻尼器具有良好的动力性能.
③ 对比分析不同电流下优化前后阻尼力和动态可调范围. 优化后阻尼器的最大输出阻尼力可达560 N,最大可调范围为4.8;优化前阻尼器最大输出阻尼力仅有253 N,最大可调范围为3.7. 进一步说明优化后的阻尼器具有更优的动力性能,验证了该优化设计方法的准确性及有效性.

