通信电台带外多频干扰预测方法与验证

王雅平，魏光辉，尚在飞, 潘晓东，万浩江

(1.陆军工程大学石家庄校区 静电与电磁防护研究所， 河北,石家庄 050003；2. 陆军第九综合训练基地， 河北,张家口 075000； 3.南京军代局驻烟台代表室，山东，烟台 264100)

通信电台是各作战单元之间的信息交互枢纽，直接影响着战争的进程. 在未来战场环境中，空间电磁场往往具有域连续不断、频域相互重叠的特点，如何预测电台在复杂电磁环境下的生存能力变得十分重要[1-3]. 国军标GJB 151B-2013给出的敏感度测试方法是在单频干扰下进行的[4]，而通信电台在工作时，往往会受到己方的无意干扰和敌方的有意干扰，直接导致电台面临多个频率干扰同时存在的情况. 因而，对通信电台进行单一频率的辐射敏感度试验不能全面反映其在真实战场环境中的生存能力，需对其进行多个频率组合干扰下的敏感度试验. 但在实际操作过程中，对所有的频率组合进行试验工作量太大，因而考虑替代方法：通过现有的单频敏感度测试结果对多个干扰信号同时存在时的干扰效应进行预测. 关于通信电台干扰问题，文献[5-8]中进行了大量的研究工作，根据不同的干扰信号形式，以不同的电台作为受试对象分析对应的效应规律. 其中，李伟等[8-9]对不同类型电台带内干扰机理进行研究，并利用电台的单频敏感度建立其双频至多频干扰的预测模型. 王雅平[10]给出了通信电台带外双频干扰效应预测模型，通过分析双频干扰叠加后的信号形式，引入占空比系数，在已知通信电台单频敏感度的前提下预测其在双频干扰下的生存能力，但该预测模型在面临三种及以上干扰信号同时存在的情况，无法从叠加信号包络推导出相应带占空比系数的预测模型. 而在研究带外双频干扰时已知，导致电台重启的干扰主要耦合通道是互连线缆[11]，并且叠加信号峰值的出现频率与干扰信号的频率有关，因此类比于接收机带内干扰效应预测方法[12]，分别给出基于干扰信号峰峰值和有效值相关的预测模型.

为了确定重启效应对应的敏感类型，提出了调幅波干扰判别方法，即利用在调幅深度一定时调幅波与正弦波之间幅值和能量具有确定的对应关系这一特性，分别利用正弦波和调幅波进行带外干扰试验来确定预测模型. 在此基础上，总结出带互连线缆这类电台在带外强场干扰下出现重启效应的预测方法. 最后利用某型电台进行带外多频干扰试验，验证该预测方法的有效性.

1 带外多频干扰预测方法

1.1 耦合机理与预测模型

已有试验表明，短波、超短波电台在带外单频电磁辐射下的效应规律基本一致[7]，当场强达到一定强度时，带外干扰效应表现为电台重启，以超短波电台为例，在最敏感频点处干扰场强达到约50 V/m时电台会重启，并且敏感频点与外接线缆长度有关. 如果干扰信号为超宽带电磁脉冲，脉冲前后沿时间分别为0.4，0.5 ns，脉冲宽度为2.5 ns时，干扰场强达到150 V/m受试电台出现重启效应. 以上的试验表明，不同的干扰信号形式均能造成电台重启，并且重启效应的主要耦合通道为电台外部的线缆. 外界干扰信号通过电源与电台之间的互连线缆耦合入电源端，导致电台的供电电源输出电压下降，不能提供24 V直流稳压. 当电源电压降至18 V以下时，电台关闭；当干扰解除电源恢复供电时，电台能够自动重启并正常工作.

根据线缆耦合规律，类比接收机带内干扰机理，提出带外干扰机理的两种假设：一种是干扰效应与受试设备所在位置的干扰信号功率相关；另一种是干扰效应与受试设备所在位置的干扰信号振幅相关. 因而，对于重启效应以上两种假设对应两种效应预测模型：一种从能量角度出发，即干扰信号场强为重启效应主导因素，即受试设备对干扰信号的有效值敏感. 另一种从信号形式出发，即干扰信号波峰为重启效应的主导因素，即受试设备对干扰信号峰峰值敏感. 两种假设所对应的效应模型如下[9].

若受试设备与干扰信号的有效值相关，则带外双频预测模型为

(1)

当外界环境中存在两种及两种以上频率的干扰信号时，式(1)可推广为

(2)

以上预测模型中，S1为预测系数，单频干扰下达到临界干扰状态时的功率为P′i，一般作为先验知识由试验测得；当两种及两种以上的干扰频率同时作用于受试系统时，各个信号对应的功率表示为Pi. 此时，如果S1≥1，则认为会出现重启效应，反之不会.

若受试设备的敏感程度与干扰信号的峰值相关，则带外双频预测模型为

(3)

式中S2为预测系数.

同理，当外界环境中存在两种及两种以上频率的干扰信号时，式(3)可推广为

(4)

式中：E′i为单频干扰时的临界干扰峰值场强；Ei代表存在多个干扰时各个信号的峰值场强. 如果由先验知识已知单频干扰下的临界值，当两种或多种干扰作用于受试设备时，如果S2≥1，则认为会出现重启效应，反之不会.

1.2 敏感类型判断方法

当外界环境中只存在一种频率的干扰时，单从效应角度无法确定受试设备是对峰值敏感还是场强敏感. 但如果存在两种及两种以上的干扰频率，由于波形的叠加，峰值出现的频率发生改变. 因而当外界环境中存在多个干扰频率时，就有必要讨论受试设备的敏感类型问题.

由于正弦调幅波经频谱分析可认为是由3个不同频率的正弦波组成，经过调幅过程的频谱搬移作用形成了载波和上下边频. 当调幅深度一定时，正弦调幅波与正弦波之间具有固定的幅值和功率对应关系，可以利用这一关系对敏感类型进行判定.

假设某一正弦波信号：

uc(t)=Uccosωct.

(5)

振幅为Uc，此时对应的平均功率为

(6)

对于一调幅波信号：

uam(t)=(U0+kaUΩcosΩt)cosω0t=

U0(1+macosΩt)cosω0t.

(7)

其载波为

u0(t)=U0cosω0t.

(8)

调制信号为

uΩ(t)=UΩcosΩt.

(9)

调幅波的平均输出功率为

(10)

当调幅波调制深度在100%时，ma=1；此时，Pav=1.5P0；之后公式推导以及试验所用调幅波均为100%调制[4]. 当分别用单频连续波和调幅波对受试设备进行干扰时，以调幅波的平均功率换算与之对应的振幅的有效值和峰峰值：

(11)

(12)

此时，有单频连续波和调幅波的振幅之比为

(13)

若干扰效应是与受试设备所处位置干扰信号的峰峰值相关，则有：Ac=Aam，即

(14)

根据以上理论分析，分别以正弦波和调幅波作为干扰信号对通信电台进行带外干扰试验，通过对比两种干扰信号造成电台重启效应时的幅度关系，即可确定受试设备的敏感类型.

1.3 预测方法

基于以上理论分析，提出对于带有互连线缆这一类电台带外重启效应的预测方法如下.

首先，进行单频敏感度测试，确定出敏感频段，并得到临界干扰阈值.

然后，确定受试设备敏感类型. 分别进行单频连续波和正弦调幅波进行干扰试验，利用式(13)(14)判定敏感类型.

之后，确定多频干扰预测模型. 如果是有效值敏感，则选式(2)所对应的预测模型；如果是峰峰值敏感，则选式(4)作为该效应所对应的预测模型.

最后，分析环境中各干扰频率的组成，利用确定好的模型计算预测系数S的值，如果S≥1，会出现效应；反之不会.

为了验证上述方法的可行性，采用某型超短波通信电台进行进行试验验证.

从式(2)(4)可以看出，当干扰频率一定时，单频临界敏感度为定值，因而分母是固定的常数. 对于双频干扰，可以做一条直线在第一象限与坐标轴划定的区域作为安全区；对于三频干扰，则是以一个平面与坐标平面划定安全区. 在安全区内的信号组合不会导致电台重启，反之可以.

2 通信电台带外干扰试验

基于以上带外干扰重启效应预测方法，在对受试设备进行带外干扰效应预测时，首先要判定设备的敏感性类别，即利用调幅波和连续波干扰试验，确定敏感类型；再对受试设备进行多频敏感度试验，通过计算预测系数S的值，验证以上预测方法的正确性.

2.1 试验配置

试验以某型超短波通信电台为受试对象，该电台以SD2815型开关电源作为供电电源. 通过预先试验得到以下结论：经单频敏感度试验知，受试设备在36～60 MHz频段和71～100 MHz频段内较为敏感；当电台出现重启效应时，受试设备的外接电缆是干扰信号的主要耦合通道，且受试设备的敏感频点与其外接线缆的长度有关；电台接地能够提高其抗干扰能力，而电台浮地只会降低其临界阈值，对敏感规律以及效应规律没有影响.

试验过程中由信号源产生所需的干扰信号，经过10 kW功率放大器后注入GTEM室中模拟干扰环境；受试设备置于GTEM室内并利用视频监视器观察接收电台的工作状态，受试电台附近放置场强计，用以读取附近场强读数. 由于试验所采用的10 kW功放的工作频率上限是100 MHz，为了尽量获得多个测试频点，试验过程中尽量使受试设备处于敏感状态，即：电台不接地且外接线缆与干扰信号电场方向平行. 试验配置如图1所示.

2.2 敏感类型测试

在此试验配置下进行敏感类型判别测试，采用81160A型任意波形发生器提供试验所需的正弦波和调幅波信号，调幅波载波频率与同组的单频连续波相同，调制频率均选用1 kHz正弦波，调制深度为100%. 在2.1节所述的两个敏感频段内取相应的频点进行单频连续波和正弦调幅波干扰试验. 试验结果见表1.

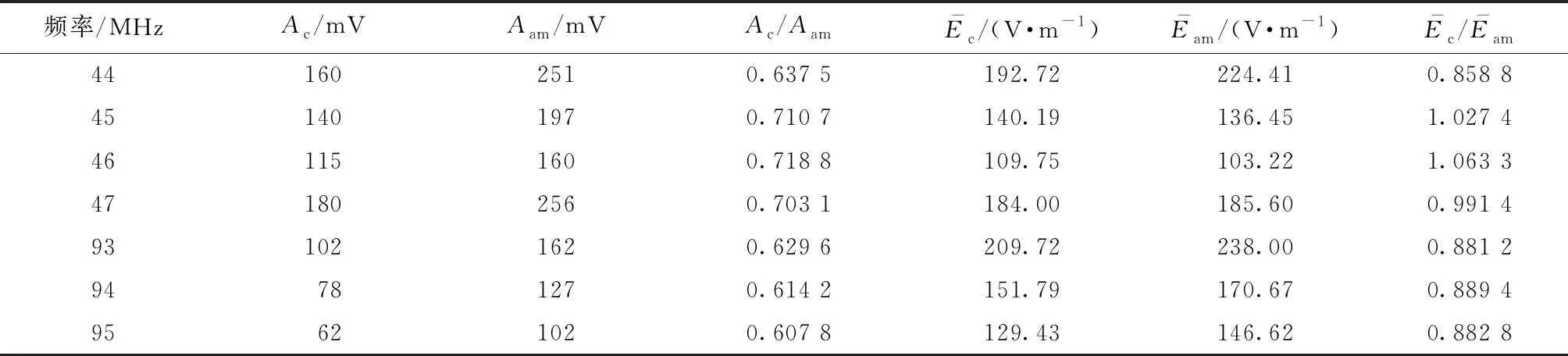
表1 正弦波和调幅波干扰试验结果Tab.1 Test results of interference tests using sinusoidal wave and amplitude modulated wave.

2.3 带外双频干扰试验

在确定受试设备的敏感类型之后，进行带外双频的干扰试验. 在图1试验配置图的基础上，采用两台AML01型号的信号发生器，分别产生两种不同频率的正弦波信号，经过功率合成后进入10 kW功放中进行放大，再注入GTEM室中进行干扰试验.

在之前试验结果确定的敏感频段内，选择两组试验频点，第一组为40,49 MHz，第二组为59,60 MHz，首先进行单频敏感度测试，试验结果如表2.

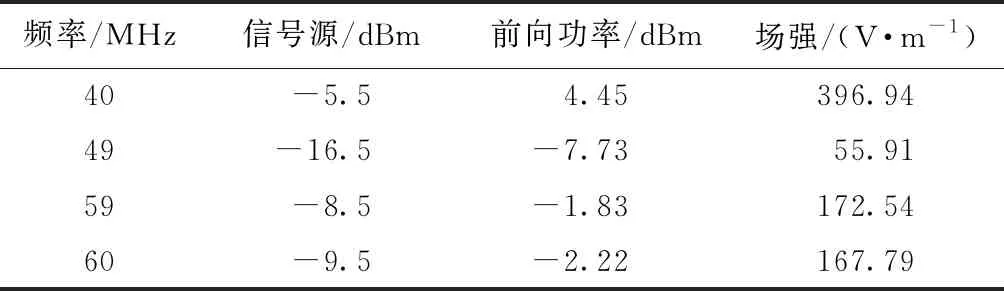
表2 单频敏感度测试结果Tab.2 Test result of single frequency sensitivity

经过单频干扰测试之后，在两个干扰频点临界干扰阈值的基础上下降6 dB进行双频干扰试验，试验过程中保持一个频点的输出功率不变，通过变化另一频点的输出功率使受试设备达到临界干扰状态，分别记录下此时两个频点对应的输出功率以及GTEM室内的场强；然后调整之前保持不变的信号的输出功率，重复之前试验过程，两组干扰频点分别得到以下试验结果，见表3、表4. 并利用表2中的试验结果和式(1)(3)，计算相对应的预测系数S1，S2.

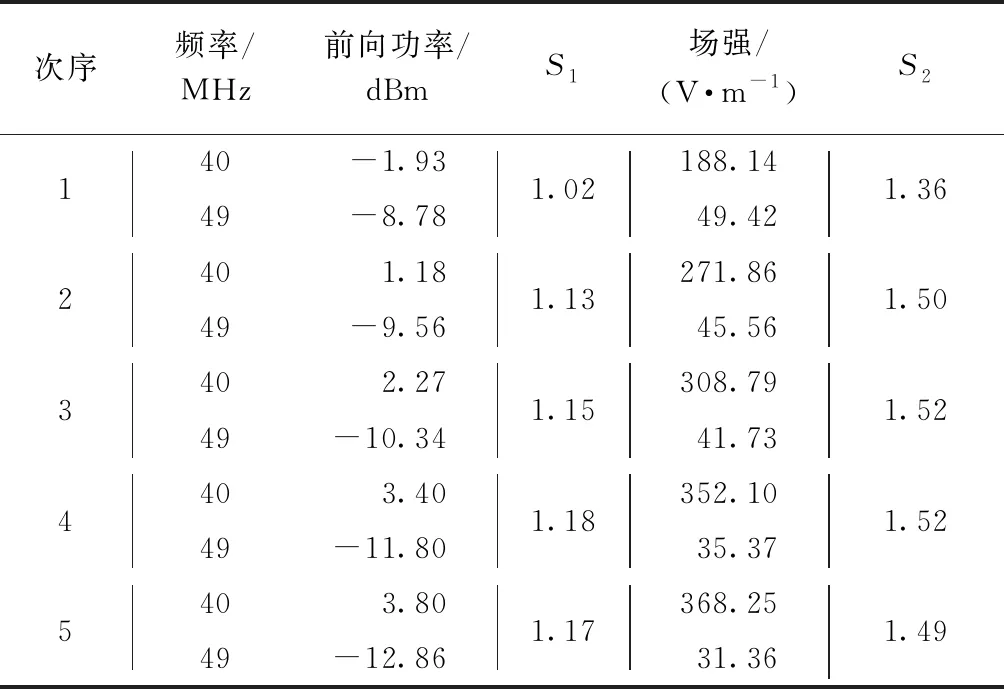
表3 双频干扰时的临界干扰阈值及预测系数(Ⅰ)

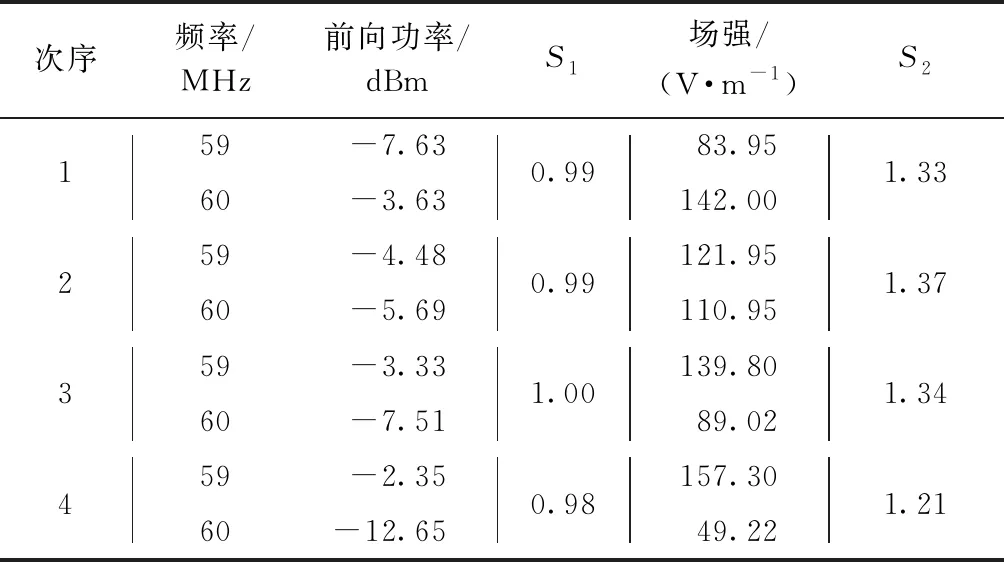
表4 双频干扰的临界干扰阈值及预测系数(Ⅱ)

由以上试验结果可以看出，有效值相关模型预测系数S1的试验误差在20%以内，而峰峰值相关模型预测系数S2的试验误差在20%～50%，说明了电台带外干扰出现的重启效应与干扰信号的有效值相关. 进一步说明了通过调幅波试验确定受试设备的敏感类型这一方法可行.

将表2～表4中的前向功率单位换算为mW，利用式(2)划定安全区域如图2. 图中直线与x轴、y轴所夹区域为安全区，如果试验结果落于该区域外则会出现重启. 双频干扰试验结果绘于图中(见圆点)，结果均落于安全区以外. 为了增加带外干扰重启效应预测模型的适用范围，进一步进行带外三频干扰试验.

2.4 带外三频干扰试验

选择同一型号的信号源进行三频干扰试验，干扰信号经过功率合成后输入功放，经功放放大后注入GTEM室中. 依旧选择两组试验频点，第一组是50、51和86 MHz；第二组是49、85和88 MHz. 首先进行单频干扰敏感度阈值试验，试验结果如表5所示.

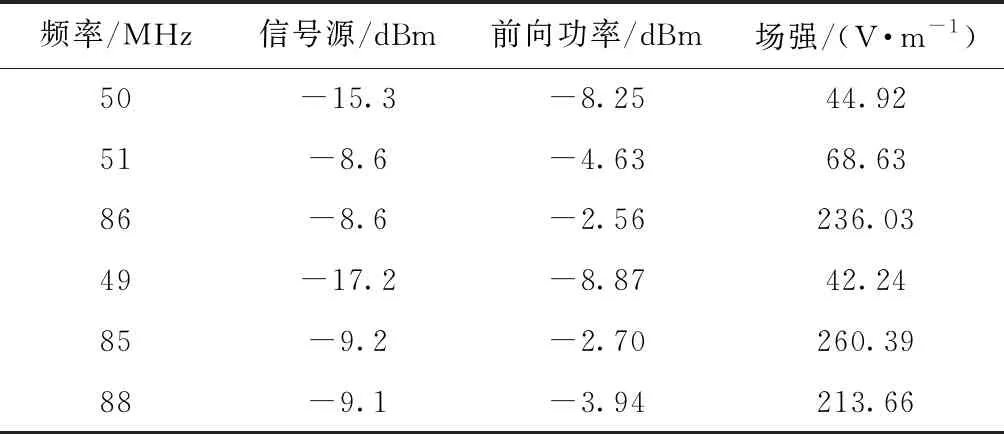
表5 单频敏感度试验结果Tab.5 Test result of single frequency sensitivity

在测得单频敏感度阈值之后，类比双频干扰试验，在3个干扰频点阈值的基础上减小12 dB，之后保持两个频点的输出功率不变，变化另一频点信号源的输出功率，使受试设备达到临界干扰状态，记录下各频点对应的输出功率和场强值；之后变化之前保持不变的频点的输出功率，重复上述过程，两组试验频点所得试验结果如表6、表7，并利用表5所得单频敏感度和式(2)(4)计算对应的预测系数.

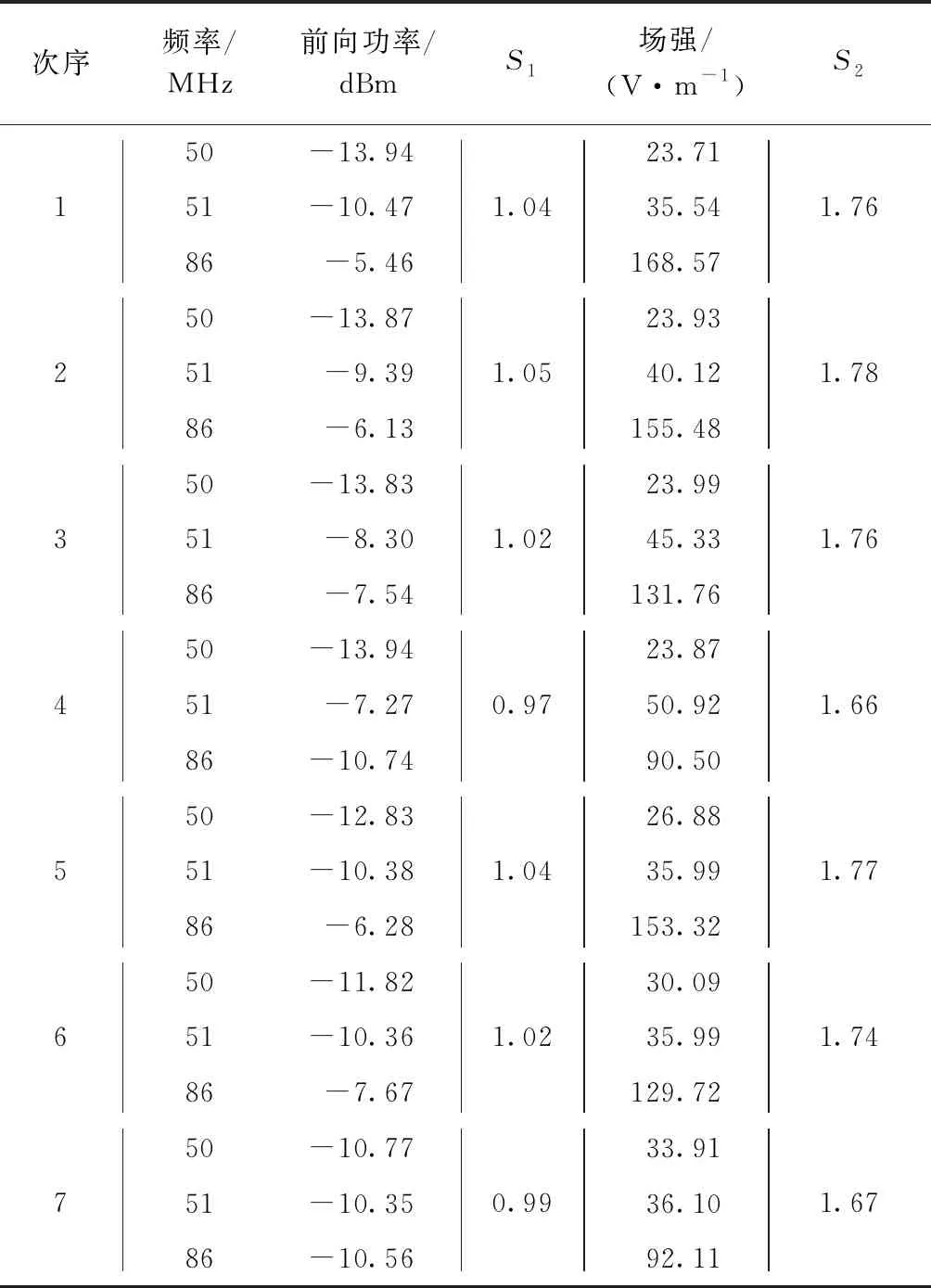
表6 三频干扰时的临界干扰阈值及预测系数(Ⅰ)

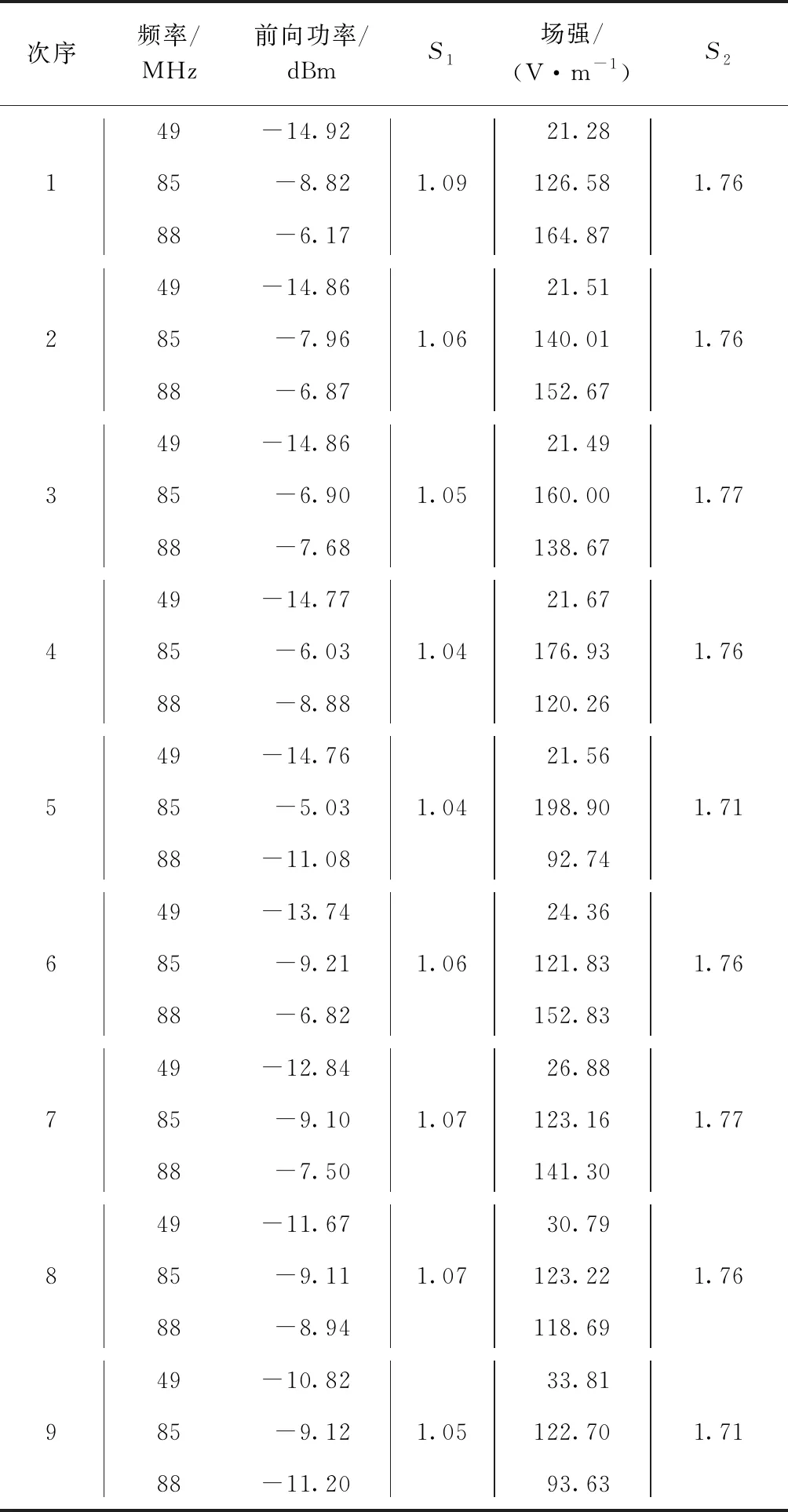
表7 三频干扰时的临界干扰阈值及预测系数(Ⅱ)

将表5～表7中的前向功率单位换算为mW，利用式(2)划定安全区域如图3和图4. 图中斜面与3个坐标平面所夹区域为安全区，如果试验结果落于该区域外则会出现重启. 三频干扰试验结果绘于图中(见灰点)，结果均落于安全区以外.

由以上试验结果可以看出，有效值相关预测模型依然适用，S1预测误差在23%以内，而峰峰值预测模型系数S2预测误差最高达到77%，而且通过理论分析可知叠加频点的个数越多，误差越大. 但不论双频还是三频干扰试验中，有效值预测模型在临界干扰状态下计算所得预测结果多数大于1，考虑到试验过程中的误差不可避免，在实际应用过程中仍存在“虚警”的可能. 但对于用频装备来说，预测结果显示其未达到临界干扰而实际测试已经达到临界干扰，这种情况在应用过程中不希望出现，因而该效应预测模型具有一定的应用价值.

3 结 论

针对电台在带外强场干扰下出现的重启效应，类比电台带内干扰的效应机理，从能量和波形的角度分别对应着不同的效应模型. 为了确定受试设备的敏感类型，提出利用正弦连续波和正弦调幅波分别进行干扰试验，利用这两种干扰信号幅值和功率之间的联系，确定敏感类型并选择需要的预测模型. 利用预测模型结合单频敏感度试验结果可以确定受试对象的安全区，并能够计算预测系数S的值. 试验所用电台经正弦波和调幅波干扰的试验结果，峰峰值的比值在0.61左右，表明电台带外重启效应与干扰信号的有效值相关；之后进行带外双频和三频试验，试验结果预测系数S1更接近于1，预测误差在23%以内，而预测系数S2的最大误差在50%～70%，且叠加的干扰频点越多误差越大. 试验结果进一步说明了带外干扰的敏感类型及敏感类型确定方法的有效性. 但是，由于此类重启效应是由于干扰通过电台间的互连线缆耦合到受试设备内部引起的，如果对于单兵背负式电台或者自带电池供电的用品设备是否适用还有待进一步研究.