磁流变阻尼器滞回性能试验与计算模型分析

赵 军, 高 宁, 李小鹏, 雷波波, 赵 毅

(郑州大学 土木工程学院,河南 郑州 450001)

磁流变阻尼器(magnetorheological damper,MRD)是一种利用磁流变效应提供可控阻尼的半主动控制器件,具有阻尼可控、功耗低、响应迅速等特点,能够对结构起到良好的减振作用[1-2]。MRD在桥梁工程中的应用较多,主要目的为实现对斜拉索的振动控制。在国内,2006年至2013年间,李金海[3]、曹宏[4]、瞿伟廉等[5]分别将MRD应用于山东滨州黄河大桥、长沙洪山大桥和岳阳洞庭湖大桥;2015年,国外学者Weber等[6]成功将MRD应用于俄罗斯岛大桥。MRD在建筑工程中的应用较少,日本将40 t MRD先后成功应用于博物馆和Keio大学建筑中[7]。

MRD对电流变化具有极高的灵敏度,电流变化的瞬间MRD阻尼力同时发生改变,因此,可通过改变供给电流的大小实时控制MRD阻尼力。近年来,学者利用MRD这一特性,将MRD应用于混凝土抗震结构以提高其抗震性能,减小地震作用下的结构响应[8-12]。相对于钢筋混凝土抗震结构,CFRP筋混凝土抗震结构可以有效减小震后残余变形,但是耗能能力相对较低[13-14]。通常采用增设耗能元件提高抗震结构的耗能能力,但是传统的耗能元件如屈曲约束支撑、软钢阻尼器及摩擦阻尼器等在受力时将产生塑性变形或永久性偏位,进而增加结构变形[15-16]。因此,在CFRP筋混凝土抗震结构中采用传统耗能元件虽然耗能能力有所提高,但是结构变形恢复性能将受到耗能元件变形的限制,无法发挥残余变形较小的优势。MRD可通过调节电流提高结构耗能且不增加残余变形,是CFRP筋混凝土抗震结构理想的耗能元件。在结构受力时增大电流提高MRD阻尼力,以提高结构的耗能能力;在结构卸载或荷载为0 kN时减小或关闭电流降低阻尼力,以降低或消除MRD对结构恢复功能的限制,实现不增大结构的残余变形。

目前,对于MRD-CFRP筋混凝土柱及剪力墙抗震性能已开展了相关的试验研究[8,10],研究表明,MRD对CFRP筋混凝土柱及剪力墙抗震性能影响较大,但是理论分析研究较少,限制了MRD在抗震结构中的应用。为开展MRD-CFRP筋混凝土柱及剪力墙抗震性能理论分析,需要首先开展MRD力学性能方面的研究。轴向往复荷载作用下MRD力学性能虽有少量试验研究成果[17],但是未考虑加载速率和电流控制方式对MRD阻尼力影响。因此,为深入研究MRD力学性能,本文将开展轴向往复荷载作用下MRD力学性能试验研究,同时考虑峰值点位移、电流大小、加载速率和电流控制方式的影响,最后提出轴向往复荷载作用下MRD阻尼力-位移曲线计算模型。

1 试验概况

1.1 MRD设计概况及工作原理

图1为MRD示意图,本文试验采用课题组制作的四线圈剪切阀式磁流变阻尼器,外部形状为圆柱体,外部缸筒高为596 mm,直径为150 mm;活塞杆直径为40 mm,行程为±40 mm。MRD内部的多级活塞有4个凹槽,每个凹槽缠绕漆包线,采用环氧树脂密封进行绝缘处理;多级活塞两端分别与活塞杆连接并穿过缸筒内部,一端活塞杆与试验装置或其附属连接件相连,另一端引出铜线与直流电源箱相连。磁流变液采用自制方法获得,其组分主要包括铁粉、硫酸钠和液体石蜡等。

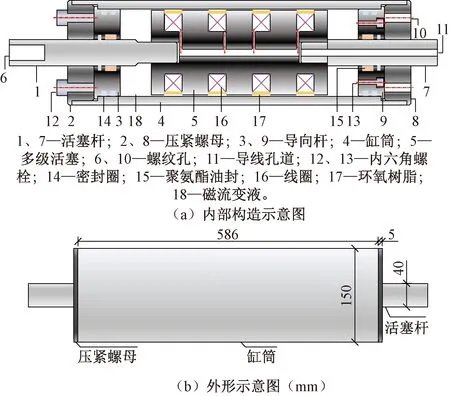
图1 MRD示意图

MRD加载过程中,活塞与缸体发生相对运动,挤压磁流变液并使其流过缸体与活塞间的间隙,调节电流可使MRD内部磁场强度改变,磁流变液黏度也随之改变[18],进而可控制阻尼力大小。

1.2 加载装置

图2为加载装置。加载设备为MTS拉力试验机,最大荷载为±200 kN,行程为±50 mm。将MRD和拉力试验机牢固连接后,MTS拉力试验机对MRD施加轴向往复荷载。

图2 MRD轴向往复荷载试验装置

1.3 加载制度

轴向往复荷载作用下MRD力学性能试验采用位移控制加载,具体加载制度如下。

(1)电流大小I和峰值点位移ΔM的影响。分别进行4组不同峰值点位移ΔM、不同电流大小I的MRD力学性能试验,各组试验加载速率v均为1.0 mm/s。4组试验峰值点位移ΔM分别为±5、±10、±20及±40 mm,每组试验均包含8个加载等级,每级进行1次往复加载,各级循环峰值点位移ΔM相同,对应的电流I分别为0、0.04、0.08、0.12、0.16、0.20、0.24、0.28 A。4组试验分别命名为I-5、I-10、I-20和I-40,加载制度如图3(a)所示。

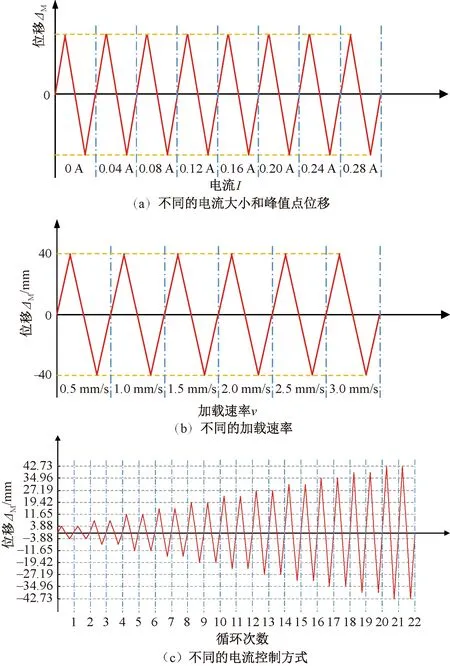
图3 加载制度

(2)加载速率v的影响。进行3组不同加载速率v的MRD力学性能试验,同时考虑了电流大小I的影响。每组试验均包含6个加载等级,每级进行1次往复加载,各级峰值点位移均为± 40 mm,每级循环加载速率分别为0.5、1.0、1.5、2.0、2.5、3.0 mm/s。每组试验电流大小I保持不变,但3组试验电流大小I不同,分别为0 、0.14 和0.28 A,3组试验分别命名为V-0、V-0.14和V-0.28,加载制度如图3(b)所示。

(3)电流控制方式的影响。分别进行4组不同电流控制方式的MRD力学性能试验。结合混凝土结构拟静力试验,试验中各级循环峰值点位移以±3.88 mm为级差逐级增加。每组试验均包含11个加载等级,每级进行2次往复循环加载。4组试验分别命名为M-0、M-0.28、M-P和M-S,其中试验M-0全程关闭电流;试验M-0.28全程保持通电,电流大小为0.28 A;试验M-P在每级循环峰值点位移处断电1次,随后继续保持通电,电流大小为0.28 A;试验M-S在每次循环在峰值点向0 mm加载过程中,加载至1/3峰值点位移处断电1次,随后继续保持通电,电流大小仍为0.28 A。加载制度如图3(c)所示。

2 试验结果与分析

2.1 电流大小对MRD阻尼力的影响

图4为试验I-5、I-10、I-20和I-40的MRD阻尼力-位移曲线图。由图4可知,由于MRD制作时磁流变液未充满阻尼器,自0 kN加载时,初始位移4～5 mm荷载增长较小,斜率趋近于零,接近于水平线,该阶段为初始位移段。随后曲线进入荷载增长段,即初始位移段之后的2～3 mm加载段,该阶段荷载急剧增加,斜率急剧增大。该阶段结束后曲线进入荷载稳定段,荷载稳定段初期时荷载略微下降,随着位移的增大,阻尼力保持稳定状态。由于试件制作缺陷以及试验I-5的峰值点位移较小,试验I-5不具备明显的荷载稳定段,呈现捏拢现象。加载至峰值点后卸载,卸载段斜率趋向于无穷大,荷载急剧下降,但位移几乎不变。

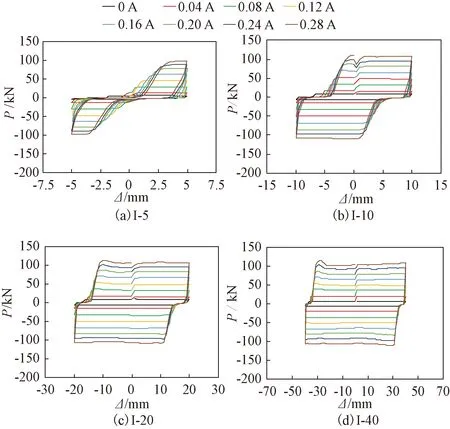
图4 不同电流大小下MRD阻尼力-位移曲线

图5为试验I-5、I-10、I-20和I-40各级循环正、反向峰值点阻尼力随电流大小变化关系图。由图5可知,I为0～0.28 A时,峰值点阻尼力随电流大小的增大而提高。I为0.04 A时的峰值点阻尼力相对0 A时提高较小;I为0.04～0.20 A时,峰值点阻尼力随着I的增大显著提高;0.20 A以后,曲线斜率略微降低,说明MRD峰值点阻尼力增幅放缓。整体而言,I为0～0.28 A时,峰值点阻尼力基本随电流大小呈线性增长,电流每提高0.04 A,峰值点阻尼力可提高16 kN。

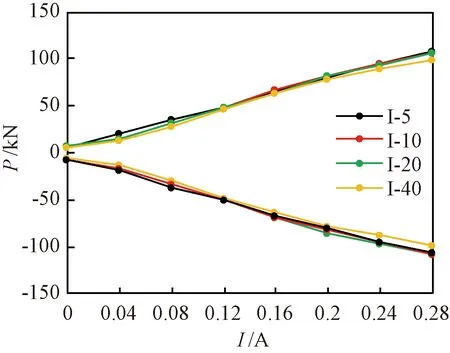
图5 峰值点阻尼力随电流大小变化关系

2.2 峰值点位移对MRD阻尼力的影响

根据试验I-5、I-10、I-20和I-40的试验结果,绘制了相同电流大小、不同峰值点位移下的MRD阻尼力-位移曲线图,如图6所示。图6(a)、6(b)、6(c)及6(d)电流大小分别为0、0.08、0.16、0.28 A。由图6可知,峰值点位移为40 mm且电流大小相同时,试验I-40各级循环的峰值点阻尼力高于I-5、I-10、I-20,试验I-20和I-10峰值点阻尼力基本相同,试验I-5峰值点阻尼力最低。相同的电流大小和加载速率下,峰值点位移小于10 mm时,MRD阻尼力较小,在峰值点位移大于10 mm时,MRD阻尼力基本维持稳定状态。说明峰值点位移小于初始位移时,峰值点阻尼力较小,大于初始位移时,峰值点阻尼力较为稳定。

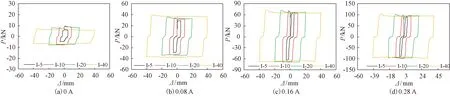
图6 不同峰值点位移下MRD阻尼力-位移曲线

2.3 加载速率对MRD阻尼力的影响规律

图7为试验V-0、V-0.14和V-0.28的MRD阻尼力-位移曲线图。由图7可知,MRD阻尼力随加载速率增大而增长。当I为0 A时,加载速率每提高0.5 mm/s,正向峰值点阻尼力提高1.6～1.9 kN,反向峰值点阻尼力提高1.7～2.1 kN;当I为0.14 A时,加载速率每提高0.5 mm/s,正向峰值点阻尼力提高2.0～4.2 kN,反向峰值点阻尼力提高2.6～4.4 kN;当I为0.28 A时,加载速率每提高0.5 mm/s,正向峰值点阻尼力提高1.3～7.1 kN,反向峰值点阻尼力提高3.1～8.9 kN。

2.4 电流控制方式对MRD性能的影响

图8为试验M-0、M-0.28、M-P和M-S的MRD阻尼力-位移曲线图。由图8可知,试验中关闭电流,随后再次供给电流且电流大小为0.28 A时,MRD在加载较短位移后,阻尼力仍然可以稳定在100 kN左右。图8(b)与8(c)曲线相似,但是由实测数据分析可知,M-P的卸载段由峰值点阻尼力急剧降至0 kN,而M-0.28则由峰值点阻尼力缓慢降至0 kN,M-P卸载段斜率相对于M-0.28更趋近于无穷大。由M-S可知,在加载过程中关闭电源,MRD将瞬间降至0 A时的阻尼力,继续通电,加载较短位移后阻尼力可重新达到稳定状态。

图7 不同加载速率下MRD阻尼力-位移曲线

图8 不同电流控制方式下MRD阻尼力-位移曲线

3 MRD阻尼力-位移曲线计算模型

3.1 模型简化

MRD阻尼力-位移试验曲线滞回环呈中心对称,正、反向曲线特征相似。图9为阻尼力-位移曲线滞回环简化模型,假设正、反向曲线完全中心对称。以图9正向加载曲线(A-B-C-D-(E)-A′)为例,曲线可分为4个阶段,即初始位移段(AB段)、荷载增长段(BC段)、荷载稳定段(CD段)、卸载段(D(E)A′段)。各阶段基本特征如下:初始位移段和荷载稳定段内阻尼力随着位移的增大变化较小;卸载段内位移变化较小;荷载增长段内阻尼力基本随位移呈线性增长。因此,可将AB段和CD段简化为水平段,D(E)A′段简化为斜率无穷大的竖直段,BC段简化为斜率为K的直线段。另外,对于D(E)A′段,若关闭电流,则曲线由卸载点首先降低至点E处,随后卸载至点A′;若保持电流不变,则曲线由卸载点直接降低至点A′处。

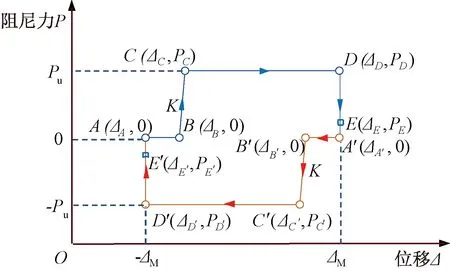
图9 滞回环简化模型

3.2 MRD峰值点阻尼力计算式

通过对各组试验每级循环正、反向峰值点阻尼力试验值的回归分析,得到峰值点阻尼力Pu与电流I和加载速率v的计算式:

Pu=364.78I+6.33v+0.024。

(1)

图10为峰值点阻尼力计算值与试验值对比图,Pu,c为计算值,Pu,t为试验值。由图10可知,计算值与试验值吻合较好,误差为1%～8%。

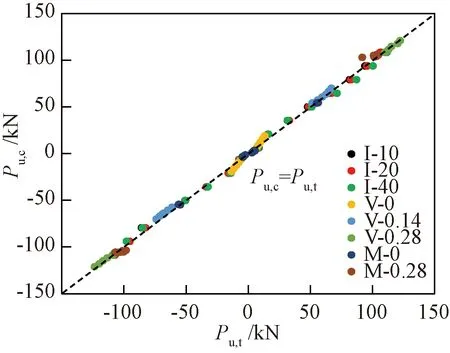
图10 峰值点阻尼力计算值和试验值对比

3.3 特征点和特征曲线计算式

(1)荷载增长段。图11分别为各组试验每级循环荷载增长段B、C点处位移ΔB、ΔC与峰值点位移ΔM分布关系图。由图11可知,ΔB、ΔC基本随ΔM线性增长。通过线性拟合,分别得到ΔB和ΔC计算式:

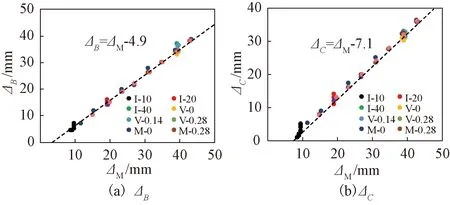
图11 ΔB、ΔC与ΔM分布关系

ΔB=ΔM-4.9;

(2)

ΔC=ΔM-7.1。

(3)

根据直线方程,由式(1)、(2)和(3)可得到荷载增长段斜率K计算式,即

K=165.80I+2.88v+0.01。

(4)

(2)关闭电流时阻尼力及再加载段。图12分别为相同加载等级下试验M-P和M-S关闭电流时MRD阻尼力与试验M-0峰值点阻尼力关系图,Pp和Ps分别为M-P和M-S关闭电流时阻尼力,Pu,0为M-0各级循环峰值点阻尼力。由图12可知,Pp和Ps与Pu,0相差较小,说明试验过程中如关闭电流,阻尼力将瞬间降低至0 A时的阻尼力,因此,断电处阻尼力,即图9中E点处阻尼力可近似为0 A时阻尼力,结合式(1),可得到关闭电流时阻尼力计算式:

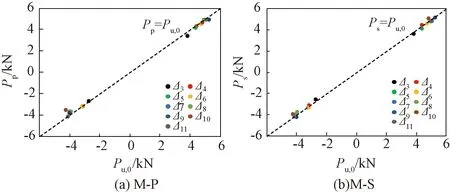
图12 关闭电流时阻尼力Pp、Ps与Pu,0关系

PE=6.33v+0.024。

(5)

图13为试验M-S同级循环断电后再加载段斜率Ks与荷载增长段斜率K关系图。由图13可知,MRD关闭电流后,再供给相同大小的电流,Ks与K较为接近,因此,可近似认为Ks与K相等,可采用式(4)进行Ks的计算。

4 模型验证

图14为试验I-40、V-0.28、M-P和M-S计算曲线和试验曲线对比图,虚线代表计算曲线,实线代表试验曲线。由图14可知,计算曲线与试验曲线具有较高的吻合度。图15为各级循环耗能计算值Ec与试验值Et对比图,其中试验M-S和M-P各级耗能试验值取2次循环的平均值。由图15可知,Ec与Et的比值为0.93～1.15,误差较小。

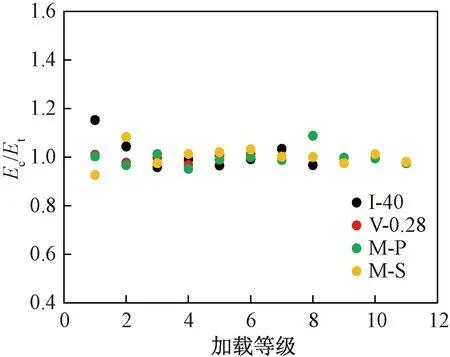
图15 耗能计算值Ec与试验值Et对比

综上所述,本文提出的计算模型在计算轴向往复荷载作用下MRD阻尼力-位移曲线时具有较高的精确度,且能够很好地描述不同电流大小、位移幅值、加载速率和电流控制方式对MRD力学性能的影响。

图14 计算曲线与试验曲线对比

5 结论

本文进行了轴向往复荷载作用下MRD力学性能试验,分析了电流大小、峰值点位移、加载速率和电流控制方式对MRD阻尼力的影响规律。

(1)相同峰值点位移和加载速率下,当电流大小为0.04～0.20 A时,MRD峰值点阻尼力随电流大小基本呈线性增长;当电流大小为0.20～0.28 A时,MRD峰值点阻尼力增长幅度逐渐减小。

(2)相同的电流大小和加载速率下,当峰值点位移小于初始位移时,峰值点阻尼力较小,大于初始位移时,峰值点阻尼力较为稳定。

(3)相同的电流大小和峰值点位移下,MRD峰值点阻尼力随着加载速率的增大而增大。

(4)在加载过程中关闭电流,MRD阻尼力瞬间降至0 A时的阻尼力,若继续供给电流,MRD阻尼力在较短的加载位移内仍能达到该电流大小下的阻尼力状态,且再加载段与荷载增长段斜率近似相等。

(5)本文提出的计算模型在计算轴向往复荷载作用下MRD阻尼力-位移曲线时具有较高的精确度,能够很好地描述不同电流大小、峰值点位移、加载速率和电流控制方式下MRD阻尼力-位移曲线变化规律。