改进的密度峰值聚类算法的差分隐私保护方案

葛丽娜, 陈园园, 王 捷,2, 王 哲

(1.广西民族大学 人工智能学院,广西 南宁 530006;2.广西民族大学 网络通信工程重点实验室,广西 南宁 530006;3.广西民族大学 广西混杂计算与集成电路分析设计重点实验室,广西 南宁 530006)

聚类分析是数据挖掘中的关键技术之一,其主要思想是将数据集划分为不同的簇,使得同一簇内的数据相似度较高、不同簇间的数据相似度较低[1]。聚类分析的广泛应用[2-4]给数据拥有者带来了巨大的利益。但是,若这些数据被攻击者截获,并恶意利用,将对数据的提供者产生不利影响,甚至危及人身财产安全。因此,如何在聚类分析中保护用户的隐私安全成为了聚类分析的一个热门方向[5]。

差分隐私是2006年由Dwork[6]针对传统的隐私保护模型无法应对新型攻击方式而提出的一种具有严格的可证明性的隐私保护模型。该模型通过对原始数据或者数据的发布结果添加符合要求的随机噪声,使得攻击者即使已知除了目标用户的数据以外的其他所有数据,也无法获取目标用户的数据,达到保护用户的隐私数据的目的。

李杨等[7]为了提高DPK-means算法的可用性,降低算法中由于添加了随机噪声而对初始聚类中心点的选取造成的影响,先将数据集均分为m个子数据集,再对各子集添加噪声后的聚类中心点进行计算,并将这些点作为初始聚类中心点,提出了IDPK-means算法,但是算法中m的值需要人为选取。

密度峰值聚类 (clustering by fast search and find density peaks, DPC)算法[8]是2014年提出的一种基于密度的聚类算法,该算法仅需输入1位参数、不存在迭代,且能够自动发现类簇中心,实现任意形状数据的高效聚类,因此广泛应用于各个领域。但是,DPC算法也存在一些不足,如输入参数截断距离的值按照经验选取、聚类中心点需要人为选取以及非聚类中心点分配采取一步策略等,并且算法存在聚类时易导致敏感数据泄露的问题。

针对改进的DPC算法的非聚类中心点分配以及算法泄露隐私的问题,本文引入可达概念,对非聚类中心点的分配策略进行改进,并在算法计算数据点局部密度的步骤中添加符合要求的Laplace随机噪声,使得算法满足差分隐私保护。

1 相关知识

1.1 密度峰值聚类算法

密度峰值聚类(DPC)算法基于以下2个假设:①聚类中心被低密度邻居数据点包围;②聚类中心与另一个密度更高的数据点之间的距离足够远。DPC算法的主要步骤包括:密度距离计算、聚类中心选取、剩余数据点分配。

Step 1 密度距离计算。DPC算法根据式(1)计算出数据点xi的局部密度ρi,当数据集规模较小时由式(2)计算ρi。由式(3)计算其到更高密度数据点的距离δi。

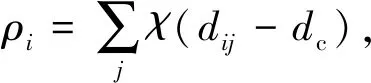
(1)

(2)

(3)

式中:dc为截断距离;dij为数据点xi到数据点xj之间的欧氏距离。dc的取值:dc的值使得数据点的平均近邻个数为整个数据集数据点总数的1%～2%[9]。

Step 2 聚类中心选取。聚类中心选取包括2种方法:①决策图法是算法根据局部密度和距离生成的以局部密度为横轴、距离为纵轴的决策图,再根据决策图人工选取最佳聚类中心的方法;②公式法[8]是根据式(4)生成决策度量γi,再将决策度量进行降序排序,选取前k个值对应的数据点作为聚类中心的方法。

γi=ρi×δi。

(4)

Step 3 剩余数据点分配。将剩余的非聚类中心点与距离该点最近并且拥有更高局部密度值的数据点归为一类。

改进的密度峰值聚类 (adaptive clustering by fast search and find of density peaks, AdDPC)算法针对DPC算法选取聚类中心点需要人为参与的问题,将加权思想引入决策度量计算中,避免了人为参与选取聚类中心点。AdDPC算法的聚类步骤如下。

Step 1 计算出数据点间的欧氏距离矩阵。

Step 2 分别根据式(2)和式(3)计算出数据点xi的局部密度ρi和距离δi的值,并对ρ和δ做归一化处理,生成决策图。

Step 3 根据式(4)计算出决策度量γ的值,归一化处理得到γ*,将γ*降序排序。

Step 4 根据式(5)计算出γ*的斜率变化率kiti,生成聚类中心点判别图:

kiti=(i-η)ki,i=1,2,…,50。

(5)

式中:η为加权因子。

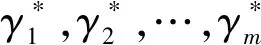
(6)

Step 6 将剩余数据点分配到拥有更高局部密度且距离其最近的点所在的类簇中。

1.2 差分隐私

差分隐私[6]是一种拥有严格数学定义以及可证明性的信息保护技术,该模型的提出基于一种假设:数据攻击者具有最大背景知识,即攻击者知道除了需要保护的敏感信息以外的所有信息。

定义1ε-差分隐私[6]。设随机算法M,对于任意2个邻近数据集D和D′,若满足式(7),则称算法M满足ε-差分隐私。

Pr[M(D)∈S]≤eε·Pr[M(D′)∈S]。

(7)

式中:Pr[·]表示事件发生的概率;S∈Range(M),Range(M)表示随机算法M的所有输出的集合;ε为隐私预算,表示隐私保护程度,其值与隐私保护程度成反比。

定义2全局敏感度[10]。设有查询函数f:D→Rd,对于任意一对邻近数据集D和D′,函数f的全局敏感度Δf为

(8)

式中:‖·‖1为1-范数距离。全局敏感度Δf表示函数f(·)在邻近数据集上查询结果的差异程度,差分隐私中所添加噪声的大小受全局敏感度的影响。

定义3Laplace机制[6]。设有随机函数f(·),f(D)为其对数据集D查询返回的输出结果,则Laplace机制定义为

(9)

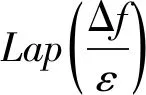
Laplace分布的概率密度函数的表达式为

(10)

2 改进的密度峰值聚类算法的差分隐私保护方案

由AdDPC算法的步骤可以看出,该算法隐私泄露的关键是局部密度ρ。若攻击者拥有除了目标数据点以外的所有数据点信息,则攻击者可以通过局部密度ρ的定义公式,计算出目标数据点与其他数据点的距离,进而推出目标数据点的相关信息。若攻击者删除数据集中目标数据点,则其余数据点的局部密度ρ会相应减小,得到其余数据点在删除目标数据点前后的局部密度差,获取目标数据点与其余数据点间的距离,从而推断出目标数据点的真实信息。

由对AdDPC算法的隐私泄露问题分析可知,当数据拥有者发布算法聚类的局部密度ρ时,可能会导致隐私数据的泄露。而本文算法在局部密度的计算过程中添加Laplace随机噪声,使得该算法满足差分隐私保护的要求,进而达到保护隐私信息的目的。

AdDPC算法的聚类原理是寻找具有较大局部密度,同时将距离其他更高局部密度点较远的数据点作为聚类中心,再将其余数据点划分到局部密度比该点大且相距较近的点所在的类簇中。当数据集分布较为均匀,或者数据集中某一类簇存在几个局部密度较大且距离其他局部密度更高的点较远的点,AdDPC算法即使选取了正确的聚类中心点,也可能会出现部分非聚类中心点归类错误的问题。在AdDPC算法中,非聚类中心点的分配是采用一步分配策略,容易引起“多米诺效应”,即密度大的数据点若分配错误会导致密度较小的数据点归类错误的问题,从而影响算法的聚类性能,如图1所示。图1(a)为Flame数据集的标准分类图,图1(b)为AdDPC算法对Flame数据集的错误聚类结果图。

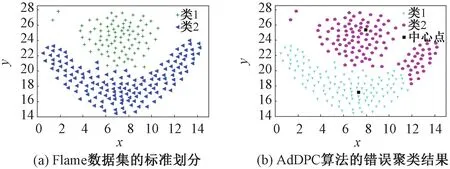
图1 Flame数据集聚类

对于AdDPC算法的非聚类中心点分配问题,本文引入DP-rcCFSFDP算法[11]中的可达定义,将其应用于非聚类中心点的归类,从而提高AdDPC算法的聚类效果,基于此,提出一种基于局部密度加噪的密度峰值聚类差分隐私保护算法(differential privacy preserving algorithm of clustering by fast search and find density peaks based on local density adding noise, DP-DPCL)。DP-rcCFSFDP算法的相关定义如下。

定义4邻域点。给定数据点pi,在以pi为圆心、E为半径的邻域中的所有数据点称为pi的邻域点。

定义5可达。给定一串数据点s1,s2,…,sn,若每个数据点si+1为数据点si的邻域点时,则称数据点sn到数据点si可达。

DP-DPCL算法具体步骤如下。

Step 1 对输入数据集预处理,初始化数据点间的欧氏距离,根据式(2)计算出数据点的局部密度。

Step 2 选取合适的隐私预算ε,根据局部密度ρ的敏感度,生成符合Laplace分布的噪声,并将随机噪声添加至局部密度ρ中,记为l_ρ。

Step 3 将l_ρ降序排序,并按照式(3)计算距离δ,根据l_ρ和δ生成决策图。

Step 4 根据式(4)计算决策度量γ,归一化后得到γ*,将γ*降序排序。

Step 5 根据式(5)计算γ*的斜率变化率kiti,生成聚类中心点判别图。

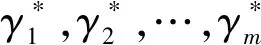
Step 7 将剩余数据点分配到与其距离更近且拥有更高局部密度的数据点所在类簇,生成初始聚类结果。

Step 8 对初始聚类结果进行遍历,若存在数据点对可达且不在一个类簇中,则将局部密度值小的数据点归类为局部密度值大的数据点所在类,得到最终的聚类结果。

在DP-DPCL算法中,局部密度每次所添加的噪声是随机生成的,而由于加噪导致输出的局部密度值不同,这样使得攻击者难以依靠获得的局部密度差值推导出目标数据点的真实信息。由于数据点到密度更高点的距离δ的值也会受到局部密度值变化的影响,从而进一步降低了隐私泄露的风险。

在DP-DPCL算法中使用的差分隐私保护技术中的Laplace机制是由算法的敏感度Δf以及隐私预算ε控制生成的满足Laplace分布的随机噪声。敏感度是指在数据集中增加或减少任意一个数据点对聚类结果的最大影响。对于任意一对邻近数据集,对2个数据集进行局部密度计算时,根据局部密度定义公式可知,数据点局部密度的最大差值为1,因此,局部密度的敏感度Δf=1。

3 实验及结果分析

3.1 算法的差分隐私性证明

DP-DPCL算法的差分隐私性证明如下:

假设数据集D和D′为一对邻近数据集,R(D)和R(D′)分别为AdDPC算法未添加噪声时作用于数据集D和D′的聚类结果,A表示任意一种聚类结果。S(D)和S(D′)分别表示在AdDPC算法中添加Laplace噪声后的作用于数据集D和D′的输出结果,B表示添加噪声后的任意一种聚类结果。则由式(7)～(10)可得

DP-DPCL算法的差分隐私性得证。

3.2 实验结果分析

本实验由Python语言编程实现,实验环境为Windows10的64位操作系统、8 GB内存、2.30 GHz处理器。实验用于测试的数据集信息如表1所示。本实验中使用F-Measure[12]和调整兰德指数ARI[13]作为评价指标。用A=(A1,A2,…,AK)表示数据集的真实划分,B=(B1,B2,…,BK′)表示聚类算法对数据集的聚类结果。

表1 数据集信息

F-Measure值是同时考虑了精确率(precision)和召回率(recall)的一种评价指标。精确率用于衡量算法聚类结果的精确程度,召回率用于衡量聚类结果的完备程度,F-Measure指标可以较为全面地区分算法的聚类能力。精确率、召回率和F-Measure分别按照式(11)、(12)、(13)来计算,F-Measure取值为[0,1],值越大聚类效果越优。一般的聚类结果分布情况有4类:Na表示在真实划分A和聚类结果B中同属一个类簇的数据对的数目;Nb表示在真实划分A中属于同一类簇,而在聚类结果B中不属于同一类簇的数据对的数目;Nc表示在真实划分A中不属于同一类簇,而在聚类结果B中属于同一类簇的数据对的数目;Nd表示在真实划分A和聚类结果B中均不属于同一类簇的数据对的数目。

(11)

(12)

(13)

若β=1,则式(13)可以化为

(14)

兰德指数(RI)是一种考虑在真实划分和聚类结果中均划分为同一类簇或均不是同一类簇,即Na和Nd这2种情况的评价指标。这种指标评价比较片面,因此对兰德指数进行改进,提出调整兰德指数(ARI)。ARI用于度量真实划分A和聚类结果B之间的相似度,其计算式如式(15)所示,取值为[-1,1],值越接近1,聚类效果越好。

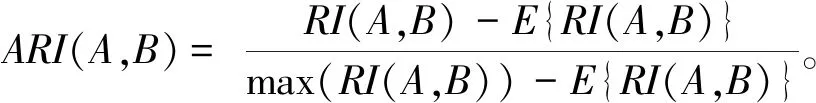
(15)

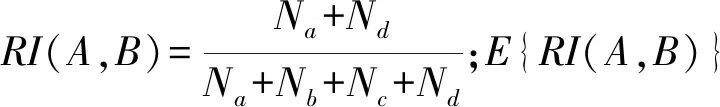
为对比算法在不同隐私预算下的聚类性能,将DP-DPCL算法与AdDPC_rDP算法、DP-rcCFSFDP算法[16]、IDPK-means算法[7]进行对比,通过算法的F-Measure和ARI指标值评估DP-DPCL算法的聚类性能。实验中DP-DPCL算法在Iris、WDBC、Aggregation数据集上的dc取值分别为2.5、1.5、2.5,邻域半径取值分别为2.2%、0.8%、0.5%,加权因子设为1.001。AdDPC_rDP算法在Iris、WDBC、Aggregation数据集上的dc取值分别为2.5、3.0、2.5。DP-rcCFSFDP算法的dc取值分别为2.5、2.5、4.0,根据文献[16],邻域半径分别为1.8%、0.7%、0.4%。IDPK-means算法中,根据文献[7],敏感度Δf=M+1,M为数据集的特征属性数,最大迭代次数Niter_max=1 000。

图2为4种算法在Iris数据集上聚类的输出结果。由图2(a)可知,随着隐私预算ε的增加,各算法的F-Measure指标值逐渐增大并趋于稳定;当隐私预算ε>1.5时,DP-DPCL算法的F-Measure达到最优,此时,在Iris数据集上DP-DPCL算法聚类性能最佳。由图2(b)可知,随着隐私预算的增加,各算法的ARI逐渐增加并趋于稳定;当隐私预算ε>1.5时,DP-DPCL算法的ARI达到最优。因此,在Iris数据集上,总体聚类性能最佳的是DP-DPCL算法。

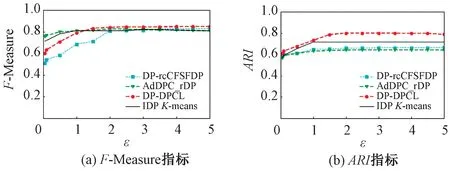
图2 Iris数据集输出结果

图3为4种算法在WDBC数据集上的输出结果。由图3(a)可以看出,DP-DPCL算法的F-Measure均优于AdDPC_rDP算法;当隐私预算ε>1.5时,DP-DPCL算法的F-Measure达到最优,其值均比其余3种算法高。由图3(b)可知,DP-DPCL算法的ARI均优于其余3种算法。

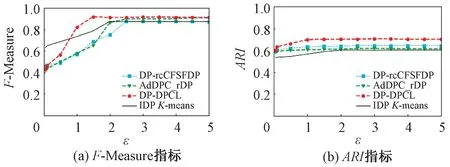
图3 WDBC数据集输出结果

图4为4种算法在Aggregation数据集上的输出结果。由图4(a)可知,当隐私预算ε>1.5时,DP-DPCL算法F-Measure均优于AdDPC_rDP;当隐私预算ε=2.0时,DP-rcCFSFDP算法的F-Measure达到最优值,此时,DP-DPCL算法的F-Measure较DP-rcCFSFDP算法小,其余情况下DP-DPCL算法均比DP-rcCFSFDP表现更佳。与IDPK-means算法的F-Measure比较可知,当隐私预算较小(ε<0.9)时,IDPK-means算法表现均比其余3种算法好,当隐私预算ε>0.9时,IDPK-means算法表现最差。图4(b)结果显示,在Aggregation数据集上,DP-DPCL算法的ARI最优。

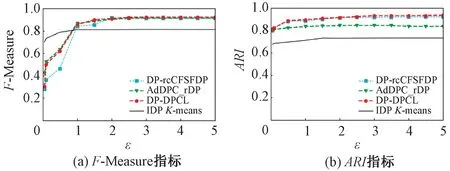
图4 Aggregation数据集输出结果

实验结果表明,总体上看,DP-DPCL算法的聚类性能与AdDPC_rDP算法、DP-rcCFSFDP算法、IDPK-means算法相比得到了提升,在不同的数据集上指标数值均优于其他3种算法。因此,DP-DPCL算法可以在保护敏感数据的同时降低所添加的随机噪声对聚类可用性的影响。

4 结论

本文针对AdDPC算法的隐私泄露问题提出了DP-DPCL算法,并对算法的非聚类中心点分配策略进行了优化。首先对AdDPC算法存在的隐私泄露问题及非聚类中心点分配策略进行分析,在算法计算数据点局部密度的过程中添加Laplace噪声,并在算法分配非聚类中心点的过程中引入邻域和可达的概念,优化算法非聚类中心点分配的方法。实验结果表明,DP-DPCL算法在隐私预算ε>1.5时,聚类性能得到了提高,这是因为隐私预算过小时,添加的噪声过大,增加了其他算法对聚类中心选取的随机性,导致剩余数据点的分配可能比原始聚类算法的更好;而当预算增大时,DP-DPCL算法对剩余数据点的分配方式进行了改进,使得更多的点分配到正确的类簇。但是,DP-DPCL算法对不同的数据集聚类时,当最佳截断距离值不同,如何自适应选取最佳截断距离值需要进一步研究。