两阶段的近邻密度投票模拟离群点检测算法

郑忠龙, 曾 心, 刘华文

(1.浙江师范大学 数学与计算机科学学院,浙江 金华 321004;2.绍兴文理学院 计算机系,浙江 绍兴 312000)

离群点检测是指从给定数据中找出或发现那些与其他数据存在明显差异的数据的技术[1]。由于能够带来诸多潜在价值,离群点检测在现实各领域有着广泛应用,如信用卡欺诈检测[2]、网络安全入侵检测[3]、安全系统故障检测[4]以及对敌人活动的军事监视[5]等。

近年来,学者们提出了许多离群点检测算法,其中以基于近邻的检测方法应用较广。该方法主要依据数据的近邻信息,判断其是否属于离群点。由于具有较强的可解释性和直观性,基于近邻的离群点检测是目前应用最为广泛的离群点检测方法之一。根据近邻信息的表示方式不同,基于近邻的离群点检测可细分为基于距离的方法和基于密度的方法。基于近邻距离的方法更关注全局离群点,而基于近邻密度的方法既能关注到全局离群点,也能有效发现局部离群点[6]。

为更好地表达现实生活中个体之间的复杂关系,并发现其中的结构团体,通常将社会关系描述成复杂网络或图的形式,其中每个节点代表一个实体,而节点之间的边则表示为实体之间的社会连接关系。社区发现是指社会网络从中发现那些紧密关系的节点的集合[7]。社区发现在现实生活中有着广泛应用,如在社交网络中挖掘具有共同兴趣或相似社会背景的群体进行内容推送[8];建立传染病网络动态模型,预测疫情发展趋势。

本文旨在利用社区发现中的消息传递机制,度量数据的密度信息,进而发掘数据中的离群点。传统的社区发现算法通过信息传递在复杂网络中交互信息,根据信息量优先识别最具影响力的节点。这与离群点检测原理一致,事实上,离群数据通常与大部分正常数据存在显著差异。因此,位于网络边缘、且对周边节点的影响力越小的节点,被认为是离群点的可能性越大。基于这种思想,本文提出了一种两阶段的近邻密度投票离群点检测算法。

本文主要创新点如下:①利用社区发现中节点之间的消息传递机制产生的影响力,提出了一种新的基于近邻关系的投票离群点检测算法;②采用随机游走技术,计算节点及其近邻的密度,以反映节点的重要程度;③节点之间的信息交互只在近邻内部发生,从而降低了计算量,使得投票决策更具有可解释性,相比于全局范围内的投票决策节省了运算时间和空间。

1 相关工作

基于密度的离群点检测算法核心思想是根据数据对象给出的某种合理阈值,形成每个数据点的邻域范围,若数据点远离各邻域,则将该数据点视为离群点。近邻密度方法对数据整体分布没有要求,在局部离群点检测上表现优异,从而得到飞速发展,其中Chen等[9]提出的K近邻算法理论成熟且逻辑简单,是目前使用最为广泛的检测算法之一。但是基于近邻密度的方法对参数选取较为敏感,此类方法的离群点检测精确度容易受到参数的影响而产生较大波动。

影响力最大化(influence maximization,IM)[10]作为消息传递机制的主要研究内容之一,广泛应用于病毒营销、谣言控制、社交计算等实际应用场景中。投票作为一种有效识别节点影响力的算法,能够快速识别核心节点以进行信息传播。VoteRank算法[11]首次使用二元组表示数据节点的投票能力与投票得分,按照一定的策略记录投票得分,发现节点影响力与投票得分呈正相关。WVoteRank算法[12]考虑到权重对节点投票能力的影响,构建加权的一阶近邻矩阵来衡量不同相似度对节点投票能力的影响程度。在此基础上,VoteRank++算法[13]同时引入一阶、二阶近邻迭代用于表示节点的投票能力。由于投票进行消息传递具有鲁棒性强、容错率高、可解释性强等优势,广泛应用于社区发现和集群检测中。然而,目前并没有直接将投票算法应用于离群点检测的相关研究。

本文受到节点影响力算法的启发,将投票模拟算法与传统离群点检测方法相结合,提出一种新颖的离群点检测算法。离群点通常位于网络边缘,且对周边节点的影响力较小,故本文选取影响力最小的数据为离群点。实验发现,本文将投票机制嵌入到离群点检测领域是一种新颖而有效的检测算法。

2 近邻投票的离群点检测

基于近邻投票的离群点检测算法包括密度估计和投票模拟2个步骤:密度估计通过随机游走进行密度迭代,得到估计密度和节点重要性;投票模拟通过重要节点传递信息,得到信息平衡时节点的信息量,将信息量最少的点视为异常点。

2.1 密度估计

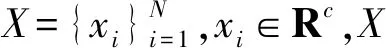
(1)

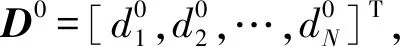
根据Q(xi),设每个数据对象与其K近邻间存在一条无向边,由此构成了以近邻关系为基础的无权图G。由图G得到邻接矩阵A:

(2)

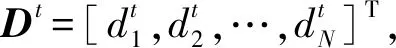
(3)

P=M-1A。

(4)

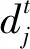
基于贡献均等和无后效性假设,随机游走可达平稳状态。具体来说,贡献均等指节点i的K个近邻对i的贡献均等,无后效性指节点i在随机游走中具有无后效性,即i在t+1时刻状态只与t时刻状态有关。任意节点i做随机游走,如图1所示,箭头方向表示节点间的有向关系。近邻节点为当前节点可直达的节点,如图1中节点2的近邻节点为节点1和节点3,节点4的近邻节点为节点2和节点3。参数α表示由任意节点i根据箭头所指的有向关系游走到其近邻j的转移概率,认为每个节点i都有均等的概率转移到其近邻节点,取值在[0,1]中;节点i直接回到自身会形成一个自环,如图1中0节点,其概率为1-α,又称回退概率。

图1 随机游走示意图

将式(3)写作向量形式得

Dt+1=αPDt+(1-α)D0。

(5)

由P的定义可知,|P|≠0,|αP|≠0,P为标准化的矩阵,则I-αP非负定。由于P每一行中非0元的个数等于K,当K>1且α∈[0,1]时,αP至少有一个非主对角元不为0、主对角元不等于1,则|I-αP|≠0,I-αP可逆。

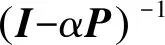
Dt+1=αPDt+(1-α)D0;

Dt=αPDt-1+(1-α)D0;

⋮

D2=αPD1+(1-α)D0;

D1=αPD0+(1-α)D0。

通过迭代可得到Dt+1关于Dt,Dt-1,…,D0的表达式:

Dt+1=αPDt+(1-α)D0

=αP(αPDt-1+(1-α)D0)+(1-α)D0

=α2P2Dt-1+αP(1-α)D0+(1-α)D0

⋮

=αt+1Pt+1D0+(1+αP+α2P2+…+αtPt)(1-α)D0。 级数展开式:

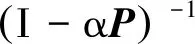
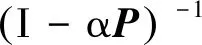
(6)

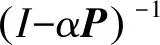
利用式(6)可以得到估计密度值Den,则近邻密度估计算法的简要描述如下。

算法1近邻密度估计。

输入:数据集X,近邻参数K,转移概率α;

输出:每个数据点的估计密度值Den。

Step 1 计算数据对象间的欧氏距离,标准化后得到距离矩阵Dist*;

Step 2 获取数据的相似性SM=I-Dist*;

Step 3 根据相似性矩阵SM,计算每个数据对象的初始密度D0,及其K近邻集Q(xi);

Step 4 利用K近邻Q(xi),根据式(2),构造邻接矩阵A,并获取概率转移矩阵P;

Step 5 根据式(6),估计数据的密度值Den。

算法1的时间主要花费在计算数据对象间的距离矩阵Dist*和计算估计密度Den,其最坏情况下的时间复杂度为O(NK+logN),其中N为数据集中数据对象的数量;K为每个数据对象的近邻个数。节点的估计密度和近邻关系是进行投票模拟的前提。

2.2 投票模拟

由于传统的异常检测算法对离群点的判别过于苛刻,易将小簇间节点视作异常,导致误判。如图2所示,图2(a)中数据对象u处于两簇间,且簇间距较小,易聚合成更大的簇,图2(b)中数据对象u位于单个簇外,远离簇中心。事实上是只有图2(b)中u点为离群点,而传统的离群点检测算法会把这2种情况下的u均视为异常。投票算法通过N轮节点信息传递,宽松对待“可能异常”数据对象,将图2(a)中u检测为正常节点,是一种容错率高的算法。

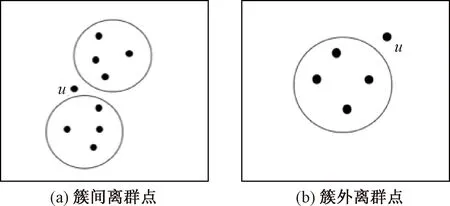
图2 2种不同离群点情况

高密度节点周围往往环绕更多节点,成为中心节点的可能性大,而中心节点对近邻影响更大,故给予估计密度最大的节点优先投票权,每一轮投票均以当前密度最大的节点为候选投票节点,辐射更多的对象。每个数据点根据相似性和密度自发投票,直到每个数据点都完成投票,统计每一轮迭代的投票结果得到投票排名。在上述背景下,模拟投票算法根据以下3种原则进行迭代:①当u为未投票节点中估计密度最大的点,且u的K近邻集Q(u)中不存在比u估计密度更大的节点,u投票给自己;②当u的K近邻Q(u)中存在比u估计密度更大的点,记与u相似性最大的点为v;③若v未投票,则u投票给v,若v投票给w,则u也投票给w。

图3为上述3种模拟投票原则。箭头方向表示投票方向,箭尾为投票者,箭头记录被投票者;点的大小为该点密度大小,正方形点是比u密度更大的候选节点;圆圈范围为u的K近邻集Q(u)。

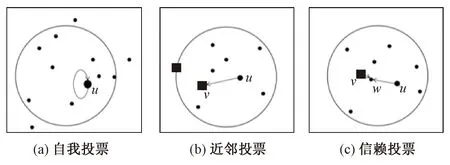
图3 模拟投票原则图解

如图3(a)所示,当u是所有未投票的节点中密度最大的点时,u的影响力最大,能够传递更多的信息给近邻节点,则u投票给自己。如图3(b)所示,v是u的邻域内比u密度更大且最近的节点,若v还未投票给其他节点,则u投票给v。如图3(c)所示,v的密度在u的K近邻集Q(u)中最大,且其影响力大于u,若v投票给了其近邻点w,则u投票给w。算法2为投票模拟(voting simulation outlier detection, VSOD)算法。

算法2投票模拟算法。

输入:各数据点的估计密度值Den,近邻点个数K,异常个数nns;

输出:离群点的索引。

Step 1 利用算法1计算密度值Den,并对其降序排列,得到投票候选节点索引voteWho;

Step 2 根据相似性SM计算每个候选点的K近邻集Q(xi);

Step 3 以voteWho索引为序,利用3种不同模拟投票原则在候选点的近邻集Q(xi)中投票,记录投票得分votescore;

Step 4 完成投票的节点跳出voteWho,直到voteWho为空;

Step 5 取votescore降序排列对应的节点索引nodeOrder;

Step 6 取nodeOrder后nns个索引。

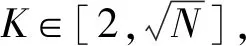
通过算法1密度估计可以得到数据点之间的相似性与密度信息,为算法2投票消息传递奠定了基础。算法2中节点排序nodeOrder反映了节点重要性,当每个数据点都迭代投票后,得到nodeOrder越靠前的数据点,成为中心节点的可能性越大,而离群点往往远离中心,故选取nodeOrder靠后的节点为离群点。

3 实验

本节对所提出的投票离群点检测算法进行了实验分析,在11个不同类型和大小的公共数据集上与其他9种离群点检测算法进行比较。这些数据集从实际应用中收集得到,广泛用于评价异常检测方法的性能,实验数据来自于UCI Machine Learning Repository网站。

3.1 数据集

表1为各数据集的基本介绍。这些数据集最初应用在分类任务中,而离群点检测是无监督的,在实验中往往将更少类标签对象视为异常,其余对象视为正常[15]。本文在实验中也遵循该原则,将较少一类作为异常类。例如WPBC数据集,有198条维数为33的数据记录,其中有47条标签为R的异常数据记录,WPBC数据集中异常数据量占总数据记录的23.74%。

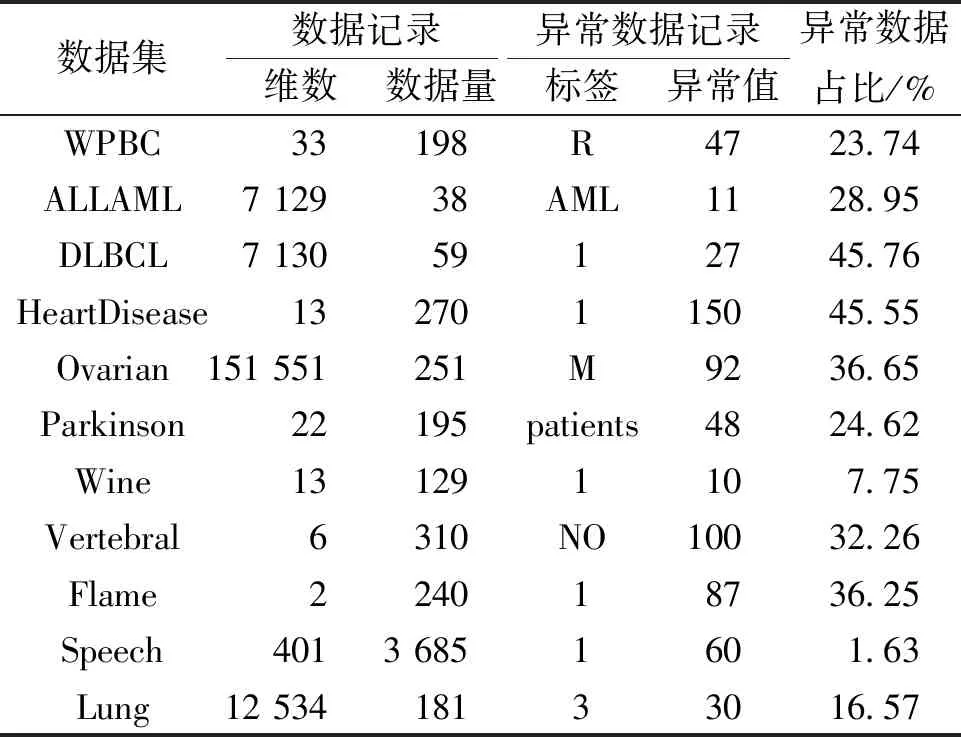
表1 实验数据简要描述

为验证本文算法的有效性,选取9种不同的离群点检测方法进行比较,实验在AMD A9-9425 RADEON R5处理器(3.10 GHz)、4 GB RAM的计算机上进行。

3.2 评价指标

不同的检测算法参数不同,算法参数的选取可能会对最终结果产生影响,因此,合适的参数对算法至关重要。为保证严谨性,实验中的每种异常检测算法的参数都被设置为原文献中建议的值或工具箱推荐的值。为便于比较各方法的检测效果,实验采用常用的3个指标:Precision、max_F1和AUC。上述3个指标值均在[0,1]中,值越大算法检测性能越好。

3.3 实验结果及分析

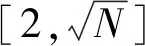
表2为异常检测算法的Precision比较。可以看出,本文投票模拟算法(VSOD)的平均精确度为79%,在大部分数据集上表现较好。在DLBCL数据集上,其他检测方法的精确度最高为62%,而所提的VSOD算法精确度为81%。此外,VSOD算法在少数数据上表现不足,但与其他传统检测算法差异不大,如在Speech数据集上,VSOD算法的精确度为90%,仍高于传统检测方法的均值89%。而Parkinson数据集更适合采用线性和降维方法检测离群点。

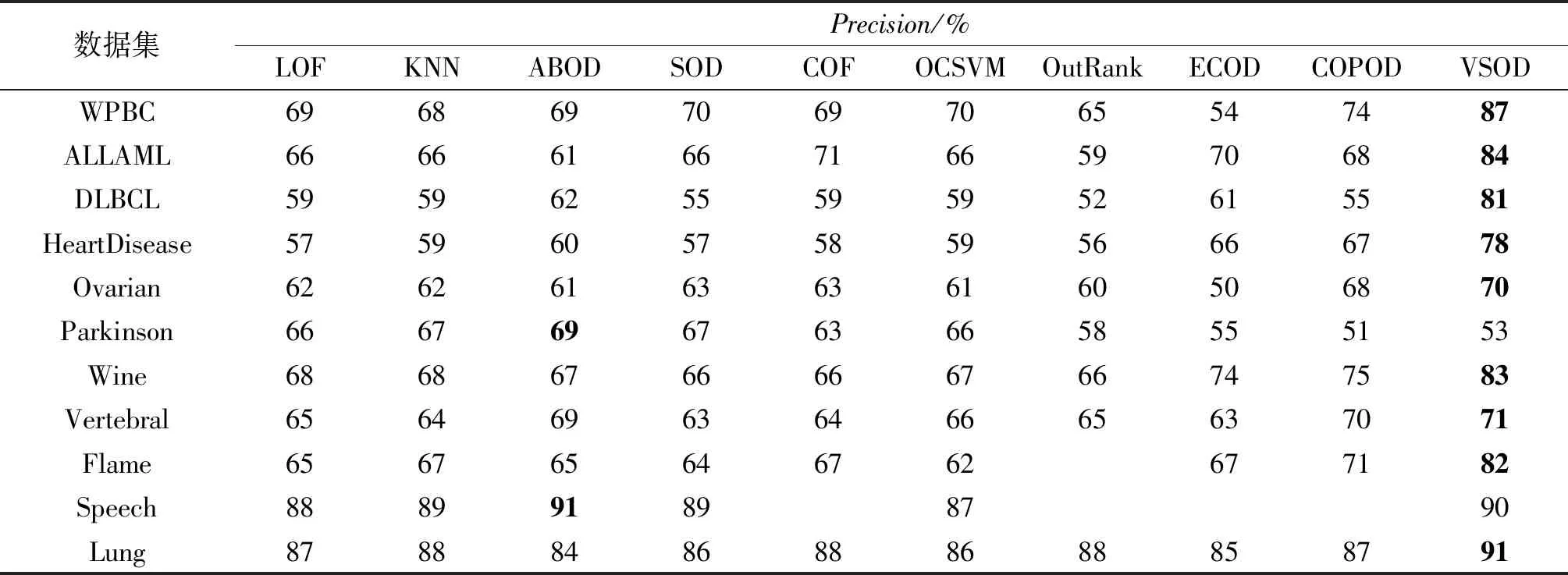
表2 VSOD算法在不同数据集上与其他算法的Precision对比

表3为9种检测方法与VSOD算法在11个特点、规模不同的数据集上的max_F1得分。可以看出,max_F1得分与表2中Precision具有类似的结论。当使用Speech数据集进行检测时,多数算法的Precision较高,但max_F1非常低,这可能是算法出现了欠拟合现象。而与其他算法相比,VSOD算法包容性强,通过与最近邻的信息交互,其Precision和max_F1得分均较高。Precision与max_F1均接近1,验证了本文算法的有效性。在这11个数据集上,VSOD算法的max_F1得分表现均较好,在ALLAML、DLBCL、HeartDisease和Lung数据集上,指标值均在80%以上。

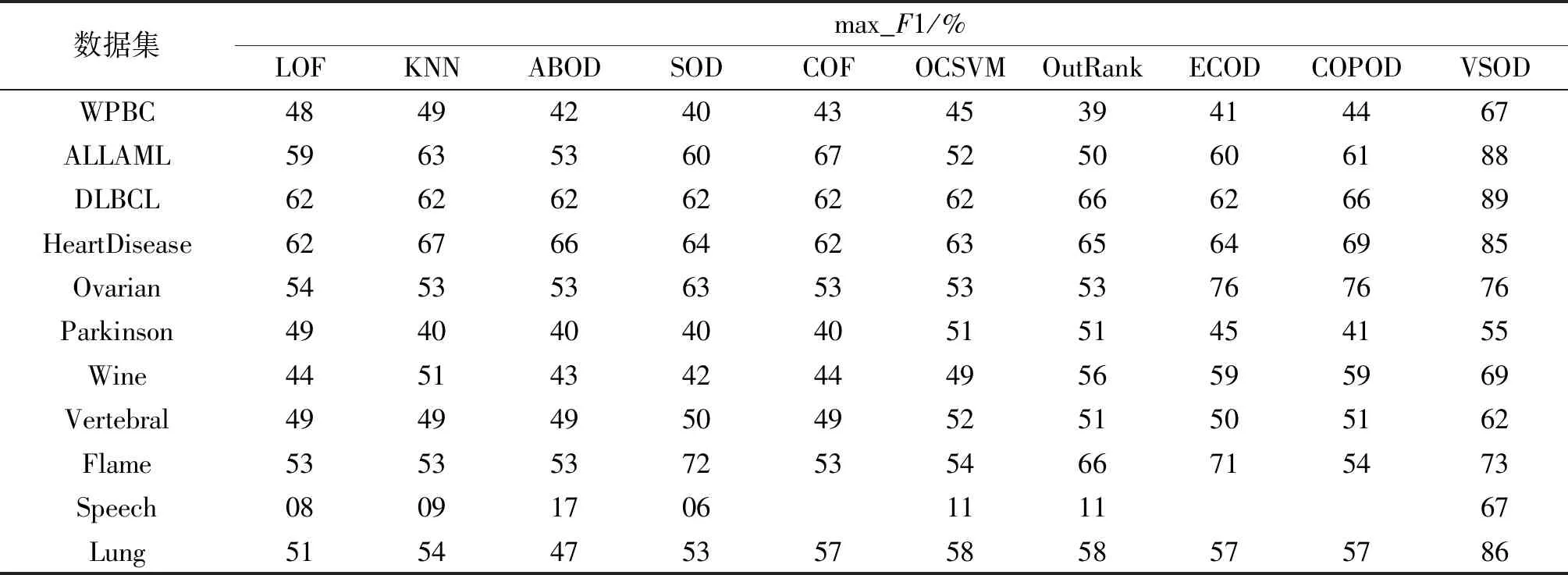
表3 VSOD算法在不同数据集上与其他算法的max_F1对比

表4给出了不同算法的AUC。在Speech数据集上,VSOD算法与ABOD算法表现相当,又明显优于其他算法。这可能是由于Speech数据集的分布不可区分,导致密度相近,容易聚集成为更大的簇类,需要严格的检测手段加以区分。在其他数据集上,VSOD算法的性能明显优于其他比较检测算法。综上,本文提出的投票检测算法是有效的。

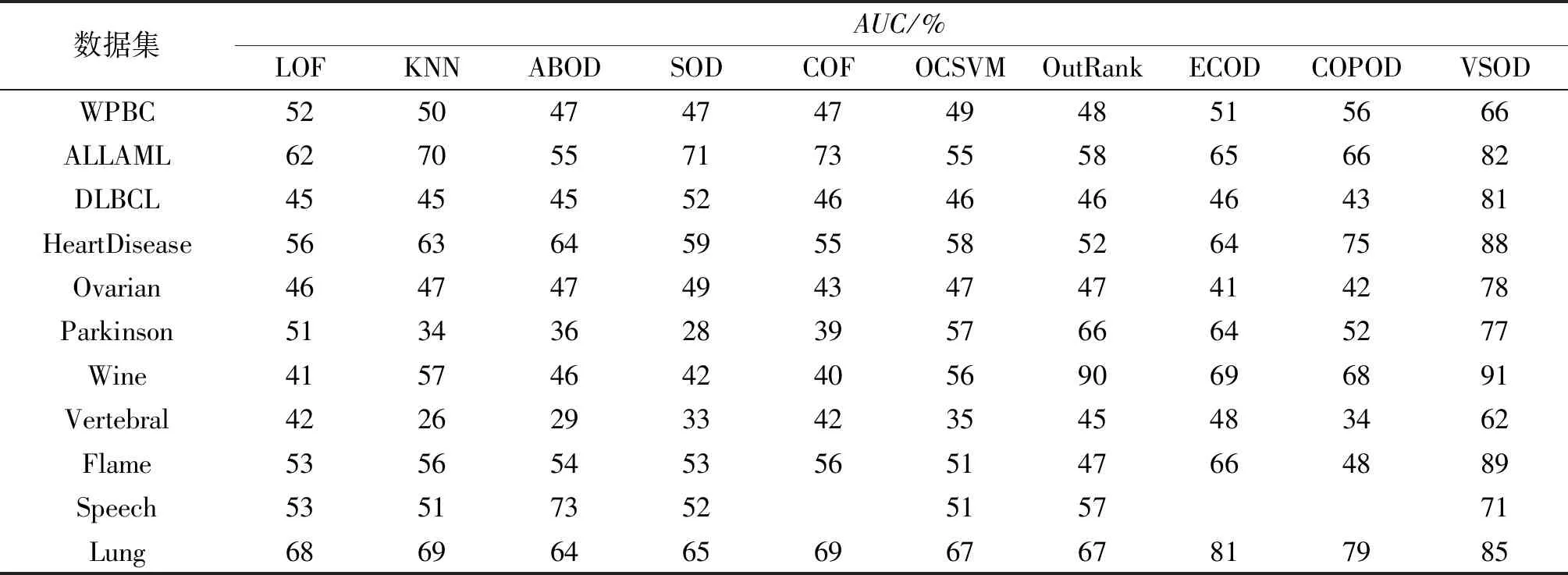
表4 VSOD算法在不同数据集上与其他算法的AUC对比

4 结论

本文提出了一种有效的异常检测方法,该方法将密度估计方法与投票算法结合,在每一轮投票中宽容算法与严格算法结合,连贯进行,相互平衡。通过在11个真实数据集上进行对比实验得到如下结论。

(1)本文结合近邻密度与模拟投票的离群点检测算法可以在一定程度上提高检测的精确度。在11个真实数据集上的实验结果表明,基于近邻的投票模拟检测算法平均精确度为79%。

(2)通过邻域内投票迭代网络信息,提高了单纯采用近邻方法进行离群点检测的算法有效性,如LOF算法和KNN算法。本文算法是一种动态信息传递过程,减少了对数据点初密度的依赖性,通过投票不断修正中心节点和离群点。

本文提出的离群点检测算法在小规模数据集上检测效果较好,但需要根据数据集在一定区间内调整K的取值才能使其达到较优效果,故下阶段将主要研究新颖的消息传递方式,从而降低算法对K值的敏感度。