*次级粘合薄磁的直线平板电磁阻尼器研究
田俊梅,王国枝,张学军,王灵梅(山西大学电力工程系,太原030009)
*次级粘合薄磁的直线平板电磁阻尼器研究
田俊梅,王国枝,张学军,王灵梅
(山西大学电力工程系,太原030009)
摘 要:为了在不改变阻尼器尺寸、形状、永磁体型号以及次级金属板材料的情况下提高阻尼力,提出了一种在次级粘合一块薄磁的方案。以一个典型的直线平板电磁阻尼器为例,利用有限元分析软件,对其气隙磁场、阻尼力以及轭板外环境磁场进行了仿真分析。仿真结果表明,次级粘合薄磁后,其x方向(次级运动方向)的阻尼力显著提高,z方向的平均阻尼力不足x方向的1%。铁磁材料轭板减小了初级永磁体外侧磁阻,降低了阻尼器外部漏磁。同时,铁磁轭板在初级磁场中被磁化,增加了阻尼器边缘磁感应强度,同样有利于提高次级在此处的阻尼力。
关键词:电磁阻尼器;有限元分析;涡流;阻尼力
划项目
随着现代工业的发展,能源自给、免维护和高可靠性的电器设备越来越受到重视[1]。永磁阻尼器作为减振设备,因其磁源稳定可靠、安全性高等特点更加适用于无需外加电源、无需人工经常维护的应用场合。文献[2]分析了一种直线平板电磁阻尼器,采用相互垂直的永磁阵列提供两个正交的阻尼力。该阻尼器永磁阵列作为次级,初级则采用单一金属材料。通过增加永磁体的厚度或极距可增加阻尼力,但同时阻尼器体积将随之增大。文献[3]和文献[4]分别分析了不同永磁阵列的直线和圆筒型电磁阻尼器,通过改变磁源布置形式改善磁场分布,进而提高阻尼力。现有文献中讨论的阻尼器初级和次级大多只采用单一材料,即采用纯永磁体和纯金属板,对复合材料的研究较少。
为了使阻尼器在不增加体积的情况下能够更加快速地消耗振动产生的能量,阻尼器在设计中需要调整结构和各项参数来尽可能的提高次级产生的阻尼力。因此,本文以直线平板电磁阻尼器为例,提出了一种次级粘合薄磁的设计,通过改变次级前端的气隙磁场分布来提高阻尼力。
1 工作原理和磁场分析
在典型的直线平板电磁阻尼器次级金属板前端
粘合一块薄磁,阻尼器结构如图1所示。

图1 直线平板电磁阻尼器结构Fig.1 Linear panel electromagnetic damper structure
1.1 工作原理
阻尼器次级金属动板在x方向运动并切割初级磁场,根据楞次定律,金属动板内部将产生涡流,并最终产生阻碍次级运动的阻尼力。特别是,当金属动板前端粘合薄磁之后,气隙磁场将受到薄磁的影响。选择薄磁厚度为几十μm时,其自身的磁能比较小,但此薄磁可以使得初级磁力线更容易聚集在金属板前端。金属板高速运行时,其本身切割磁场的速率较快,不考虑集肤效应和涡流磁场对初级磁场的作用,则金属板中感应电动势以及最终产生的阻尼力将很大。但当金属板低速运行时,薄磁作用凸显,它有效吸引金属板运动前方的磁力线,金属板将等效切割比只有初级磁场大得多的复合磁场,因此次级在低速运动时也将产生较大的阻尼力。
1.2 磁场分析
对该阻尼器中的永磁体均匀地平行磁化,则可使用等效面磁荷模型[5-7]分析永磁体产生的气隙磁场。等效磁荷模型如图2所示。

图2 永磁体的等效磁荷模型Fig.2 Equivalent magnetic charge model of permanent magnet
在空间任一点上,单位面积磁荷产生的磁感应强度为:

式中:μ0是真空中的磁导率;r为磁荷到空间任意位置的距离;er为r的单位矢量。另,σm为等效的面磁荷密度,在数值上等于永磁体的磁化强度M。
设永磁体在空间任一点的磁感应强度只是x 和z方向的函数,则等效面磁荷+σm产生的磁感应强度B+σm的x和z轴分量为:

式中:

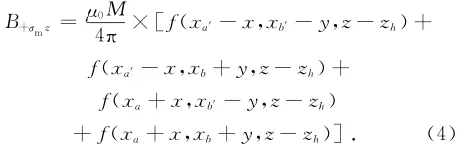
式中:
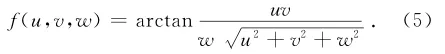
式中:x,y,z为空间任意位置的坐标;xa,xa′,xb,xb′为永磁体二维顶点坐标值。
等效面磁荷-σm产生的磁感应强度B-σm的x 和z轴分量求解方法可参照式(2)-式(5),则每块永磁体产生的磁感应强度为:
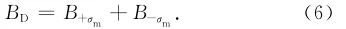
式中,BD为单块永磁体产生的磁感应强度。
对于不同数量永磁体的初级永磁体阵列,在计算整体气隙磁场时,需要对每块永磁体产生的磁感应强度叠加。再加上次级薄磁的影响,可得出气隙磁感应强度Bδ:

式中:B1为初级永磁体磁感应强度;B2为次级永磁体磁感应强度。
设次级只在x方向运动,则阻尼力为[2,8]:

式中:σ是金属动板电导率;vx是金属动板沿x轴的运动速度;a,b,c分别为金属动板x,y,z方向的有效长度。
因此,由式(7)可知,次级粘合薄磁后,气隙磁感应强度为初级永磁体和次级薄磁磁感应强度的矢量和,而又由式(8)、式(9)可推导出阻尼力和磁感应强度分布有关,因此薄磁的加入可改变阻尼力变化曲线,并由于局部磁感应强度增加而使得阻尼力增大。
2 有限元仿真
利用有限元分析软件ANSOFT MAXWELL建立直线平板电磁阻尼器二维模型,仿真分析了次级分别在有无薄磁时的阻尼力、气隙磁场,以及轭板是否为铁磁物质时阻尼器外部漏磁和对阻尼力的影响。仿真模型中阻尼器各参数如表1所示。

表1 阻尼器参数Table 1 Damper’s Parameters
2.1 阻尼力
令次级金属板以10mm/s的速度沿x轴正方向运动,可得出非铁磁轭板、次级无薄磁时和非铁磁轭板、次级有薄磁时的阻尼力曲线,如图3,图4所示。
从图3和图4的比较可以看出,次级粘合薄磁之后,次级产生的阻尼力有明显变化:
1)粘合薄磁后,x方向的阻尼力幅值明显增大,从30.6N上升为2 150N。计算其平均值,无薄磁时为17.6N,有薄磁时为754.5N。
2)粘合薄磁后的x方向阻尼力出现了与初级一侧永磁体数量相同的极值,阻尼力波动范围较大。

图3 非铁磁轭板、次级无薄磁时阻尼力曲线Fig.3 Damping force of the damper withoutferromagnetic yoke and sheet PM
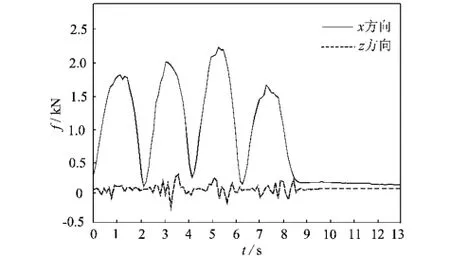
图4 非铁磁轭板、次级有薄磁时阻尼力曲线Fig.4 Damping force of the damper with sheetPM but not ferromagnetic yoke
3)次级在金属板前端粘合薄磁,其影响也主要集中在金属板前端。当薄磁随着金属板离开初级最左端时,薄磁对阻尼力的影响将迅速减弱。如图4所示,当次级运动到9~13s时,薄磁离开阻尼器,次级阻尼力大幅减小,降低至次级只有金属板时的阻尼力水平。
4)由于薄磁的影响,z方向的阻尼力将比纯金属板产生的更大,这就使得阻尼器在设计时需要增加一定的润滑或机械限位机构。但通过计算,薄磁次级产生的z方向平均阻尼力只有2.7N,远远小于x方向的平均阻尼力754.3N,因此次级粘合薄磁还是相当有意义的。
2.2 气隙磁场
如图3所示,当次级采用纯金属板时,最大阻尼力出现在5.6s,此时的阻尼器磁感应强度分布如图5所示。
如图4所示,当金属板粘合薄磁后,最大阻尼力出现在5.2s,此时的阻尼器磁感应强度分布如图6所示。

图5 非铁磁轭板、次级无薄磁时磁密分布图Fig.5 Flux density distribution of the damper without ferromagnetic yoke and sheet PM

图6 非铁磁轭板、次级有薄磁时磁密/T分布图Fig.6 Flux density distribution of the damperwith sheet PM but not ferromagnetic yoke
比较图5和图6,无薄磁时阻尼器中磁感应强度最大值约为2.26T,出现在初级一侧相邻永磁体分界面的边缘处;而当金属板粘合薄磁之后,阻尼器中的最大磁感应强度达到了4.82T,出现在次级薄磁和金属板分界面的边缘。金属板前端磁感应强度增大,由式(8)和式(9)可知阻尼力有所增加。
当轭板为非铁磁材料时,取图1中的路径l1,有无薄磁时的磁密分布曲线如图7和图8所示。路径l1为次级在运动过程中和初级永磁体所夹的气隙。由于次级运动的速度将影响初级磁场在金属板中的透入深度,因此首先分析金属板上下两侧磁场分布。
图7和图8所示的曲线族为多条曲线相叠而成,每条曲线分别对应次级运动过程中不同时刻的路径l1上的磁感应强度。
如图7所示,路径l1上的气隙磁密并没有随着次级的运动而有明显的变化。其最大值出现在初级一侧相邻永磁体的分界面,与图5所示结论相符。如图8所示,路径l1上的气隙磁密幅值除了出现在初级一侧相邻永磁体的分界面外,还随着次级的运

图7 无薄磁时路径l1的磁密分布曲线Fig.7 Flux density distribution on path l1of the damper without sheet PM
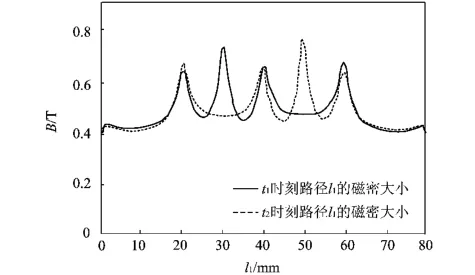
图8 有薄磁时路径l1的磁密分布曲线Fig.8 Flux density distribution on path l1of the damper with sheet PM
动出现在金属板前端粘合薄磁附近。图8中标示了任意2个时刻t1和t2的磁密分布曲线,可以看出粘合薄磁的次级在行进过程中会出现比纯金属板次级多一个的峰值。
当轭板为非铁磁材料时,取图1中的路径l2,有无薄磁时的磁密分布曲线如图9和图10所示。

图9 无薄磁时路径l2的磁密分布曲线Fig.9 Flux density distribution on path l2of the damper without sheet PM
路径l2为次级在运动过程中的中心线,是初级磁场在次级金属板中最难透入的部分。图中亦为次级运动中不同时刻的路径l2上磁感应强度构成的曲线族。
如图9所示,路径l2上的磁密依然对次级的运

图10 有薄磁时路径l2的磁密分布曲线Fig.10 Flux density distribution on path l2of the damper with sheet PM
动反应不明显。磁密分布曲线比较光滑,磁场变化率有限。图10中标示了任意2个时刻t1和t2的磁密分布曲线,从图中可以看出薄磁处的磁密发生突变,次级前端磁场变化率高。薄磁处的磁密数值也非常高,约为图9中初级磁场基础数据的3倍以上。2.3 轭板材料对阻尼器的影响
分别采用环氧树脂和纯铁作为轭板的材料,分析距离轭板5mm处路径l3的环境磁场,如图11和图12所示。图中同样为次级运动过程中不同时刻的路径l3上的多条磁感应强度的曲线族。

图11 轭板为环氧树脂时路径l3的磁密分布Fig.11 Flux density distribution on path l3of the damper with epoxy yoke
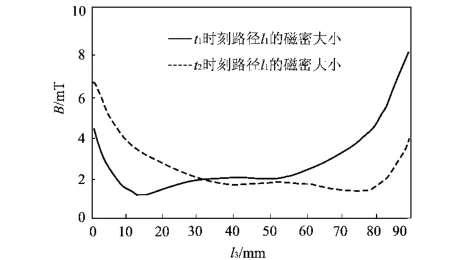
图12 轭板为纯铁时路径l3的磁密分布Fig.12 Flux density distribution on path l3of the damper with iron yoke
如图11所示,轭板为非铁磁材料时,虽然次级中有永磁体在运动,但阻尼器外部磁场基本没有变化。并且路径l3上的磁感应强度幅值出现在路径靠近中心的部分,也就是距离阻尼器边缘1/3长度的位置。按照仿真模型尺寸,距离阻尼器5mm左右的磁感应强度幅值大约为220mT。
如图12所示,当轭板采用铁磁材料时,随着次级的运动,路径l3上的磁感应强度有比较明显的变化。磁感应强度幅值出现在次级还没有到达的阻尼器边缘,这是由于次级薄磁在行进过程中改变了初级磁场分布,薄磁为初级磁场磁力线提供了通路,因此阻尼器外的漏磁有所降低。距离阻尼器5mm左右的磁感应强度幅值大约为12mT,不到非铁磁材料轭板外产生漏磁的10%。
图13为纯铁轭板、次级有薄磁时阻尼力曲线。

图13 铁磁轭板、次级有薄磁时阻尼力曲线Fig.13 Damping force of the damper with sheet PM and ferromagnetic yoke
从图13和图4的比较可以看出,当阻尼器的轭部采用铁磁材料时,由于铁磁材料在初级磁场中被磁化,气隙中的磁场将增强,次级产生的x方向阻尼力大幅提高。尤其结合图12的结论,次级粘合薄磁后阻尼器外部漏磁减少,同时内部磁场增强,因此图13中阻尼力的最大值出现在阻尼器两侧边缘附近。但从图13也可以看出,阻尼器z方向力的幅值也会提高,这将导致阻尼器次级更大的振动。
3 结论
本文从改变阻尼器次级材料的角度出发,提出了一种次级金属板前端粘合一块薄磁的电磁阻尼器。利用解析方法分析了改变阻尼器气隙磁场对阻尼力的影响,并利用ANSYS MAXWELL对阻尼器进行了仿真分析。
通过对不同轭板材料、次级是否加薄磁等多种情况进行分析,得出了阻尼器在粘合薄磁后阻尼力提高、轭板采用铁磁材料时阻尼器内外磁场分布改变同时使得阻尼力增加的结论。该阻尼器也有2个缺点,第一是其x方向的阻尼力波动较大,第二是z方向的阻尼力有所增加。但从阻尼器整体减振效果而言,更大的x方向阻尼力会使得运动机构快速定位,而其z方向阻尼力平均值依然维持在较低水平。
为了更有效的消耗振动能量,轭板和次级材料、阻尼器的结构需要综合设计,以使得阻尼器在提供更大阻尼力的同时增加使用寿命,尽可能做到无人看管以及无需更换。
参考文献:
[1] 徐文青,王忠民,张延波.采用振动能量技术的稳压电源设计[J].山东理工大学学报:自然科学版,2014,28(5):20-23.
[2] 张赫,寇宝泉,金银锡,等.平面电磁阻尼器的特征分析[J].中国电机工程学报,2013,33(21):138-144.
[3] Kim Y,Lee H,Wang S,et al.Design of a new linear magnetic damper for shock-absorbing from crash accident of high speed vehicles[C]∥Proceedings of the 12thBiennial IEEE Conference on Electromagnetic Field Computation.Miami,USA:IEEE,2006:240.
[4] Ebrahimi B,Khamesee M B,Golnaraghi F.Permanent magnet configuration in design of an eddy current damper[J].Microsystem Technologies,2010,16(1):19-24.
[5] 尹华杰,何云.永磁电机永磁体的等效模型[J].微电机,2004,37(6):14-18.
[6] 王有林,刘景林,丁冲.电磁阻尼器涡电流的计算分析[J].微电机,2006,39(2):29-31.
[7] 王有林,刘景林.电磁阻尼器设计研究[J].西北工业大学学报,2006,24(3):358-362.
(编辑:刘笑达)
[8] Sodano H A,Bae J S,Inman D J,et al.Concept and model of eddy current damper for vibration suppression of a beam[J].Journal of Sound and Vibration,2005,288(4):1177-1196.
Linear Panel Asymmetric Electromagnetic Damper of a Sheet Permanent Magnetic Added on the Secondary
TIAN Junmei,WANG Guozhi,ZHANG Xuejun,WANG Lingmei
(Department of Electrical Engineering,Shanxi University,Taiyuan030009,China)
Abstract:To increase damping force without changing damper's size and shape,permanent magnetic (PM)type,and secondary metal materials,the study proposed a new damper's design of adding a sheet PM on the secondary.As an example,a typical linear panel asymmetric electromagnetic damper was simulated with finite element analysis software in terms of air gap magnetic field,damping force,and external magnetic field of yoke.The simulation results indicate that when the secondary is added by a sheet PM,the damping force of x direction(secondary moving direction)increases significantly and the average force of z direction is less than 1%of the x direction.Ferromagnetic material yoke reduces the outboard magnetic resistance of primary PM,and also reduces external leakage of the damper.At the same time,the ferromagnetic yoke is magnetized in the primary magnetic field,which increases the marginal magnetic flux density of the damper and the damping force of the secondary at this position.
Key words:electromagnetic damper;finite element analysis;eddy current;damping force
作者简介:田俊梅(1980-),女,山西太原人,硕士,讲师,主要从事电磁机构在新能源发电与智能电网中的应用,(E-mail)dongrantina@126.com,(Tel)13994290268
基金项目:山西省科技重大专项:大规模间歇式新能源并网技术开发(20111101048);国网山西省电力公司晋电发展(2014)88号综合计
收稿日期:*2014-12-31
DOI:10.16355/j.cnki.issn1007-9432tyut.2015.03.020
文献标识码:A
中图分类号:TM359
文章编号:1007-9432(2015)03-0347-05

