变换域函数空间下周期非均匀积分与重构方法

王卫江，蔡雪滢，王佳童

(北京理工大学 信息与电子学院，北京 100081)

信号的采样和重构是信号处理和通信领域中最为重要的基础理论. 采样如同一座桥梁，将连续的模拟信号与离散的数字信号联系在一起. 在诸多采样模型中，周期非均匀采样信号模型广泛应用于各领域[1-2]. 周期非均匀采样信号在傅里叶变换域的重构方法对于非平稳信号处理效果不佳，因为非平稳信号在傅里叶变换域表现出非带限、能量非聚焦的特性，但在特定参数下的线性正则变换域[3]可以呈现带限、能量聚焦的特性，因此作为傅里叶变换广义形式的线性正则变换及其变换域的时频分析工具近年来吸引了广泛的关注，线性正则变换域的周期非均匀采样理论也被深入研究[4-11]. 2008年，Tao等[7]提出如果信号f(t)在参数M=(A,B,C,D)下为线性正则变换域内带宽为ΩM的带限信号，那么它可以由无限个周期非均匀采样点τkn=tk+nLT,k=1,2,…,L,n=…,-1,0,1,…,T=πB/ΩM准确重构. 重构公式如式(1)所示

(1)

其中

(2)

当M=(cosθ,sinθ,-sinθ,cosθ)时，上述采样定理退化为Wei等[8]提出的推论1. 当L=2,ΩM=π,t0=0.7,t1=0.9时，合成函数的时域波形如图1所示.

在实际应用中，只能获得有限个数的采样点[7]，而从图1中可以看出，该合成函数是缓慢衰减的，因此式(1)并不适用于信号的准确重构. 针对这个问题，Tao等[7]利用有限个周期非均匀采样点提出了一个重构公式，但是该公式只适用于在线性正则变换域下带限的chirp周期延拓信号. 最近，Wang等[10]利用线性正则变换域的多通道滤波器组理论提出了一种基于线性正则变换域函数空间的周期非均匀采样算法，其重构函数在采样通道数不少于线性正则尺度函数支撑区间长度的条件下可具备紧支撑的特性. 换言之，构造紧支撑重构函数所需的采样通道数会随着尺度函数支撑区间的长度线性增加，这将使得该算法在某些应用场合耗费过多的硬件资源.

本文将周期非均匀采样模型拓展到了周期非均匀积分模型，在此模型下提出了相应的重构算法. 通过引入分段积分窗函数增加了自由度，利用这个自由度可以保证该算法构造的重构函数具有紧支撑特性，并且积分通道数不受线性正则尺度基函数支撑区间的任何约束. 仿真结果表明该算法与其他算法相比可以降低插值误差，减少资源开销，提高重构性能.

1 线性正则变换基础理论

1.1 离散时间线性正则变换

x[n]为模拟连续信号x(t)以Δt为采样间隔得到的离散采样序列，即x[n]=x(nΔt). 该采样序列x[n]在参数M=(A,B,C,D)下的DTLCT表示如下[12]

(3)

式中ω表示线性正则变换域的数字频率，与连续线性正则变换中的线性正则变换域频率μ的关系为

ω=μΔt.

(4)

相应的离散时间线性正则逆变换定义为

(5)

两个离散序列x[n]和h[n]的线性正则卷积操作可分解为两个时域信号先进行解调再进行传统卷积最后进行调频，即

(6)

(7)

为了简化问题，本文统一将采样间隔Δt设为1.

1.2 线性正则域的内插与抽取分析

L倍的内插是在已知抽样序列x[n]的相邻抽样点之间等距地内插(L-1)个零点，L称为内插因子，输出序列y1[n]与输入序列x[n]的关系为

(8)

序列y1[n]的采样间隔为

Δty1=Δtx/L.

(9)

y1[n]的DTLCT[13]可以表示为

(10)

N倍的抽取是在已知抽样序列x[n]中每隔(N-1)个点取一个点，N称为抽取因子，输出序列y2[n]与输入序列x[n]的关系为

y2[n]=x[Nn].

(11)

序列y2[n]的采样间隔为

Δty2=NΔtx.

(12)

y2[n]的DTLCT[13]表示为

2 周期非均匀积分与重构方法

2.1 周期非均匀积分模型

将区间[0,L]分割为L个任意的子区间Im，m=0,1,…,L-1，L≥2. 定义周期非均匀积分为

(14)

该周期非均匀积分模型如图2所示，其中

注意到，由式(14)定义的周期非均匀积分可以重写为

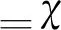
2.2 线性正则函数空间的周期非均匀积分定理

(16)

成立. 根据周期非均匀积分模型，提出如下信号重构定理.

证明首先，令函数φ(t)在区间[0,N]上是紧支撑的，将区间Im分割为任意的N个子区间I′ml，此时重新定义ωm(t)为分段函数

(17)

已知对于任意的信号f(t)∈VM存在一组权值系数{ck}k∈∈l2()使得式(16)成立，于是将式(16)带入式(14)中，可以得到

(18)

(19)

将式(19)带入式(18)中，得到

(20)

然后，交换积分号和求和号的位置可得

(21)

将n′=kL-n代入式(21)中有

(22)

(23)

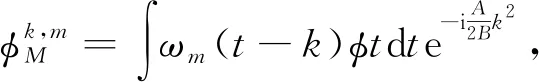
因此，将式(24)代入式(22)中，可以得到

(25)

根据式(5)(7)中的线性正则变换域卷积的定义，式(25)在时域可以表示为

(26)

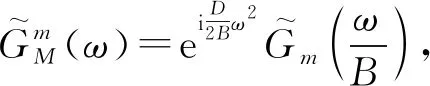
根据式(17)，滤波器系数可被重写为

(27)

式中

(28)

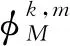
最后，给出合成函数和重构公式的表达式. 根据多通道滤波器组的准确重构性质，可得

(29)

那么，对于任意的f(t)∈VM，将式(29)代入式(16)中可得

(30)

(31)

所以，所有的合成函数均可由L个基本函数进行位移而得到.

定理得证.

3 仿真结果

本节将通过仿真实验来证明提出的基于线性正则变换域函数空间的周期非均匀积分与重构方法的有效性和优越性. 换言之，想要验证当积分通道数小于函数φ(t)支撑长度时，该算法提出的合成函数仍然是紧支撑的，可以完成信号的准确重构且性能优越. 选择三阶B-样条函数作为尺度函数，即

(32)

因为φ(t)的支撑区间为[0,3]，采用Wang等[10]提出的周期非均匀采样方法，采样通道数L不能小于3才能够保证重构函数是紧支撑的. 然而，在周期非均匀积分模型下，积分通道数L<3仍然可以构造紧支撑的重构函数. 因此选择L=2，I0=[0,1]，I′00=[0,0.4]，I′01=[0.4,0.7]以及I′02=[0.7,1.0](如图5所示)，I1=[1.3,2.0]，I′10=[1.3,1.5]，I′11=[1.5,1.8]以及I′12=[1.8,2.0].

可以验证

(33)

是非奇异的，其逆矩阵为

(34)

同理可以得到

(35)

及其逆矩阵

(36)

假设希望通过选择合适的窗函数使得

(37)

及

(38)

为线性正则变换域共轭正交镜像滤波器(conjugate quadrature mirror filter bank, CQMFB)的分析滤波器组，系数αml可以由如下计算

(39)

及

(40)

得到. 于是窗函数可以表示为

(41)

以及

(42)

综合滤波器表示为

(43)

以及

(44)

重构函数表示为S0k(t-2k)和S1k(t-2k)，其中

S0(t)=0.36φ(t)+0.72φ(t+1)+0.36φ(t+2)，

(45)

以及

S1(t)=-0.36φ(t)+0.72φ(t+1)-0.36φ(t+2).

(46)

时域波形如图6所示.

从图中可以看出该重构函数是紧支撑的.

现在考虑一雷达回波信号模型，

(47)

在验证所提出算法的过程中，选取调频率k=1，ρ0=0.5，ρ1=0.7，ρ2=0.9，τ0=1.2，τ1=2.2，τ2=5.2，f0=0.05. 容易看出，此信号带限于参数M=(1,1,0.5,1.5)下的线性正则变换域. 根据线性正则变换域的均匀采样定理，均匀采样的间隔T应小于等于πB/(2πf0)，这里选择T=1 s.

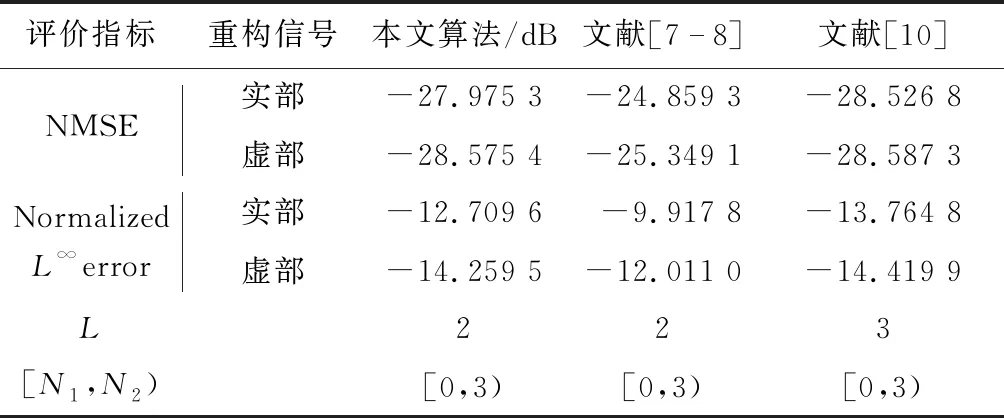
表1 本文算法与其他算法的重构性能对比

仿真结果表明，本文提出的周期非均匀积分算法在重构性能上优于其他传统算法[7-8]. 因为本文构造的重构函数S0(t)和S1(t)具备紧支撑的特性，而算法[7-8]重构函数不具备此性质，所以在有限个采样点数的情况下，具有紧支撑重构函数的算法比具有高旁瓣和缓慢衰减速率的重构函数算法重构误差要低. 尽管与Wang等[10]提出的算法(L=3)相比性能有稍许降低，但是本文提出的算法(L=2)在构造紧支撑的重构函数时，积分通道数可以不受尺度函数φ(t)支撑区间的约束. 这就意味着在选取相同的线性正则尺度函数的前提下，本文算法将使用更少的通道数，从而节约更多的硬件资源.

4 结 论

本文提出了基于线性正则变换域函数空间的周期性非均匀积分与重构算法. 通过引入高自由度的分段积分窗函数，该算法不仅可以构造具有紧支撑特性的重构函数，而且积分通道数不受尺度函数支撑区间长度的约束. 仿真结果证明该算法的重构性能优于其他传统算法[7-8]，并且能够节约更多的硬件资源. 本文提出的算法可应用于图像超分辨率重构[8]、多通道合成孔径雷达成像[14-15]等领域.