主轴系统建模与刀尖点频响函数预测研究*

刘成颖，刘 巍，郑 烽，张 智，张 洁

(1.清华大学 a.机械工程系；b.精密超精密制造装备及控制北京市重点实验室，北京 100084；2.电子科技大学 机械电子工程学院，成都 611731)

主轴系统建模与刀尖点频响函数预测研究*

刘成颖1a,1b，刘 巍1a,1b，郑 烽2，张 智1a,1b，张 洁1a,1b

(1.清华大学 a.机械工程系；b.精密超精密制造装备及控制北京市重点实验室，北京 100084；2.电子科技大学 机械电子工程学院，成都 611731)

为了获取稳定性叶瓣图所需要的刀尖点频响函数，基于响应耦合子结构分析法(RCSA)提出一种主轴系统建模方案。根据电主轴系统在实际使用过程中变化与不变化的部分将系统划分成主轴-刀柄基座、刀柄悬伸部分-刀具夹持部分和刀具悬伸部分三个子结构，并利用锤击实验、有限差分法、逆RCSA方法以及Timoshenko梁模型仿真获取各子结构的频响函数。这种模型不仅避免了复杂的结合面建模与参数识别过程，而且能简单、快速、准确地通过刚性耦合预测出不同刀柄-刀具组合下的刀尖点频响函数。以170XDS20Z11型电主轴系统为研究对象，对以上建模方法进行了实验研究，验证了本方法的实用性与准确性。

响应耦合；频响函数；子结构；预测

0 引言

在高速铣削加工过程中，机床的颤振是限制加工效率和影响加工表面质量的重要因素。目前，普遍采用叶瓣图来预测各种加工参数下颤振是否发生，而叶瓣图的准确绘制依赖于机床主轴系统刀尖点频响函数的准确获取。通常采用实验模态分析的方法获取刀尖点频响函数，这种方法对于实际应用中不同的刀柄-刀具组合，需要重复大量测试，不仅耗时费力，而且影响机床的正常生产加工。为此，国内外许多学者通过对主轴-刀柄-刀具系统的建模提出了各种刀尖点频响函数的预测方法，其中，响应耦合子结构分析法(RCSA)是最有效的方法之一。

Schmitz等[1]首次将RCSA方法引入到刀尖点频响函数预测研究中，成功预测了不同长径比刀具的刀尖点频响函数。在此基础上，他开发了三代RCSA方法(半解析法)，对子结构划分以及刀柄-刀具结合面模型进行了改进，提高了预测的准确度[2-3]。随后，Namazi和Altintas采用均布平动和扭转弹簧对主轴-刀柄锥形结合面建模[4]。Ahmadi对刀柄-刀具结合面采用连续的弹性界面层建模等优化了结合面建模方法[5]。Özsahin等通过对刀具非对称刀齿部分的精确计算与建模增强了刀具模型的合理性[6]。与结合实验测量的半解析法不同的是，Ertürk等[7]提出了一种全解析方法，将主轴系统中的各个子结构利用梁模型替代，而后利用RCSA方法耦合预测刀尖点频响函数，进一步研究了轴承和结合面对刀尖点频响函数的影响[8]。国内学者在结合面参数识别上进行了大量研究，闫蓉等[9]以均布弹簧-阻尼单元对刀柄-刀具结合面建模，采用实验和仿真结合的方法识别了结合面刚度和阻尼，李孝茹[10]和王二化[11]分别采用遗传算法和粒子群优化算法识别了结合面参数，提高了刀尖点频响函数的预测精度。

上述研究中，通常对主轴系统根据结合面进行子结构的划分，同时需要对结合面进行复杂的建模和参数识别，计算量大，而且容易引入误差。在实用性上，全解析法由于其模型简化会带来较大的预测误差，可靠性有待验证；传统半解析法预测吻合度较高，但对于不同的刀柄-刀具组合，都需要对其结构进行重新分析计算，仍然难以做到简单、快速地预测刀尖点频响函数。本文提出的预测模型巧妙避免了结合面建模过程，采用锤击实验、有限差分法、逆RCSA方法以及Timoshenko梁模型仿真获取各子结构的频响函数，并作为主轴系统特征参数存储于数据库中，根据不同的刀柄-刀具组合调用相应的子结构频响函数，通过简单的刚性耦合即可快速预测刀尖点频响函数。

1 主轴-刀柄-刀具系统建模方案

如图1所示，机床主轴系统包括主轴、刀柄(包括刀柄基座和刀柄悬伸部分)、刀具(包含夹持刀杆、悬臂刀杆和刀齿部分)。

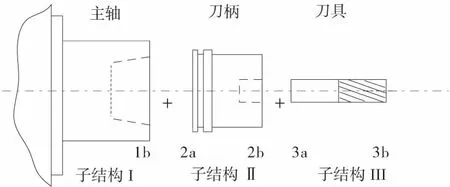
图1 主轴系统子结构划分

对于一台机床而言，在实际使用中需要更换不同的刀柄-刀具组合，对于不同的刀柄，与主轴结合的刀柄基座部分却是相同的，同样，对于与同一刀柄搭配的不同刀具，其结合部分变化也很小。因此，可以将主轴-刀柄-刀具系统划分成主轴-刀柄基座(I)、刀柄悬伸部分-刀具夹持部分(II)和刀具悬伸部分(III)三个子结构，分别获取不同的刀柄对应的子结构II的频响函数和不同刀具对应的子结构III的频响函数并储存于数据库中。

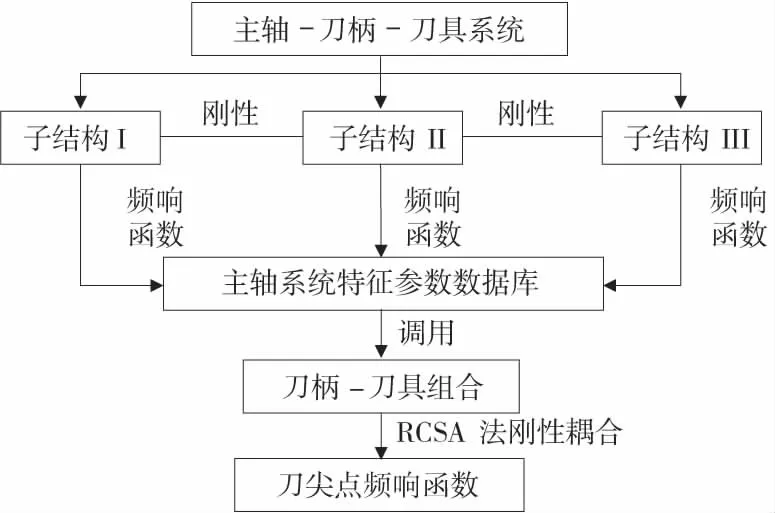
图2 刀尖点频响函数预测流程图

如图2所示，在实际应用中调用不同刀柄-刀具组合对应的子结构频响函数，利用RCSA刚性耦合理论即可快速、准确地预测刀尖点频响函数。

1.1 RCSA刚性耦合理论

如图3所示，子结构A和子结构B刚性耦合为子结构C，下面以该图示结构为例说明两子结构RCSA刚性耦合的原理。对于子结构A而言，考虑两个自由度(平动和转动)时，其频响函数矩阵可以表示为：

(1)

(2)

式中，[Aij]表示j点单位激励下i点的响应，其中各元素表示的频响函数为：Hij表示j点单位力作用下i点的位移响应；Lij表示j点单位力矩作用下i点位移响应；Nij表示j点单位力作用下i点转角响应；Pij表示j点单位力矩作用下i点转角响应。

同理可以给出子结构B的频响函数矩阵[B]，根据两个子结构在结合处的平衡条件和相容性条件，可以利用矩阵[A]、[B]推导得到矩阵[C]，如式(3)和式(4)所示[7]。

(3)

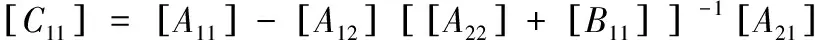
(4)

在RCSA刚性耦合理论中，为了得到装配体频响函数，首先要准确获各子结构的频响函数。以下利用RCSA刚性耦合理论讨论如何准确获取图1中3个子结构的频响函数。

图3 两结构刚性耦合示意图

2 子结构频响函数获取方法

2.1 子结构I频响函数

假设图1所示子结构II和子结构III的频响函数已知，则可由式(4)耦合得到II-III组合体的频响函数矩阵[R]，记为：

(5)

利用锤击实验获取I-II-III装配体末端3b点处频响函数G3b3b，由式(4)得：

G3b3b=R3b3b-R3b2a(R1b1b+R2a2a)-1R2a3b

(6)

利用上式反求可得R1b1b(逆RCSA法)：

R1b1b=R2a3b(R3b3b-G3b3b)-1R3b2a-R2a2a

(7)

然而，G3b3b矩阵中只有位移频响H3b3b可以直接实验获取，与转动自由度相关的频响函数则采用间接计算获取。如图4所示，激励1点，分别测量相距s的1、2、3点的位移响应获取位移频响函数H11、H21、H31，利用二阶有限差分法可知，当s较小时，转角可由式(8)求得，从而求出N3b3b。

(8)

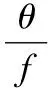
(9)

图4 转动自由度相关频响函数测试方法

对于s的选择，既不能太大又不能太小，太小会增加测量难度和相对误差，太大则会增大有限差分法的误差，一般s/l不宜超过0.04，其中l表示结构的长度[12]。

根据频响函数矩阵的互易性原理有：

N3b3b=L3b3b

(10)

(11)

由以上推导可知，由子结构II和III的频响函数可以反求得到子结构I的频响函数。

2.2 子结构II频响函数

如图5所示，为了方便测量，现将子结构II利用圆棒延长成子结构IV(刀柄-圆棒)，获取子结构IV的频响函数矩阵后，利用式(7)和圆棒频响函数矩阵反求得到子结构II的频响函数矩阵。以下推导如何利用锤击实验获取子结构IV的频响函数矩阵。

图5 子结构IV频响函数测量示意图

由式(1)和式(2)可知对于两端自由的子结构其频响函数矩阵包含16个元素。由锤击实验可直接获取4个位移频响函数H11、H12、H21、H22，且矩阵内部关系有：

(12)

因此，获取矩阵元素的关键在于获取Nij，即如何通过实验间接测量转角响应。

如图5所示，选取子结构IV两端6个测量点，间距均为s。在端点1、2处分别采用向后和向前二阶有限差分方法，可以推导得转角频响函数表达式(13)。

(13)

式(13)中共包含12个位移频响函数。由此可得实验测量方法：①敲击1点，分别测量1、1a、1b、2、2a、2b点的响应；②敲击2点，分别测量1、1a、1b、2、2a、2b点的响应；而后由式(12)和式(13)可获取子结构IV的频响函数矩阵，进而可反求得到子结构II的频响函数。

2.3 子结构III频响函数

子结构III包含刀杆和刀齿两部分，刀杆部分相当于圆柱梁，其频响函数可以通过欧拉梁或者Timoshenko梁模型仿真获取。Timoshenko梁模型由于其考虑了梁的转动惯量和剪切效应，比欧拉梁模型适用性更广而且容易操作。表1是直径同为16mm不同长度的高速钢圆棒自由模态实验与两种梁模型仿真结果对比(固有频率相对误差对比)。

表1 两种梁模型误差对比

由表1结果可知，Timoshenko梁模型与实验结果吻合度很高，而欧拉梁模型误差较大，而且随着圆棒长度减小，误差越来越大。因此，本模型选用Timoshenko梁模型仿真获取子结构III的频响函数。其中刀齿部分直径按刀杆直径的80%近似等效。

至此，电主轴系统中三个子结构的频响函数获取方法均已推导完毕，下面基于以上理论开展实验并预测刀尖点的频响函数。

3 实验研究

实验在170XDS20Z11型电主轴试验台上进行，搭配HSK-E40刀柄，实验先用高速钢圆棒替代刀具获取子结构频响函数，再安装刀具进行刀尖点频响函数预测研究。

3.1 I-II-III装配体3b点处频响函数测量

将直径为16mm，长度为120mm的高速钢圆棒装夹在刀柄上，悬长72.5mm。圆棒弹性模量为210GPa，密度为7800kg/m3，材料阻尼为0.0015，泊松比为0.3。如图6所示，实验采用PCB 086C01型力锤按照图4所示方案对1点施加激励，采用Kistler 8778A500微型单向加速度传感器拾取测量点的振动信号，力锤和加速度传感器同时连接到LMS SCADAS Mobile(SCM05机箱)采集设备，实现对信号的同步采集。

图6 锤击实验系统

利用LMS Test.Lab软件的锤击实验模块实现对实验过程的监测和数据的处理，每组实验重复五次，实验过程中尽量保证每次测量的结果基本一致，最后取其平均值。通过实验测量的位移频响函数H11、H21、H31结合式(10)、式(11)可计算出图4中3b点处转角频响函数N3b3b和P3b3b，如图7所示，图中三条频响函数曲线形状相似，幅值呈一定比例关系，模态频率基本相同。

图7 点3b处频响函数H3b3b、N3b3b和P3b3b

3.2 子结构II频响函数测量

如图8所示，从主轴上取下刀柄-圆棒组合体，近似看成子结构IV，将其置于软垫上模拟水平方向自由边界条件，按照图5所示方案进行实验，共测量12个位移频响函数，由式(12)、式(13)可求得子结构IV的频响函数矩阵，进而利用逆RCSA法即可算得子结构II的频响函数矩阵。

图8 刀柄-圆棒组合体频响函数测试示意图

子结构III的频响函数由Timoshenko梁仿真获取，而后根据式(7)可反求得子结构I的频响函数，最后将三个子结构的频响函数存入数据库用于后续刀尖点频响函数预测。

3.3 刀尖点频响函数预测

由图2可知，对于不同的刀柄-刀具组合，只需要从数据库中分别调用其对应的子结构频响函数，采用RCSA刚性耦合理论将三个子结构耦合连接即可快速得到刀尖点频响函数。

用上述方法分别预测悬长为70mm的圆棒端点和悬长为100mm的高速钢铣刀刀尖点频响函数，并与实测值(模态频率及对应负实部幅值)进行比较，如图9和图10所示。

由图9和表2可以看出，圆棒端点频响函数预测曲线与实测曲线符合得较好，其固有频率偏差几乎为零，非固有频率处幅值偏差也很小，在固有频率处，由于幅值变化剧烈，误差会明显增大，但总体来说，具有较高的预测精度。

(a)实频特性曲线

(b)虚频特性曲线图9 圆棒端点预测与实测频响函数对比

模态阶次123预测频率/Hz87710982072实测频率/Hz87710952071相对误差/%00．270．05预测幅值μm/N1．171．351．36实测幅值μm/N1．011．091．08相对误差/%15．8423．8525．93

随后，将高速钢铣刀替代圆棒进行刀尖点频响函数预测，如图10所示，铣刀刀尖点频响函数预测曲线与实测曲线也符合得很好。由于铣刀长度大，刚度小，0～4000Hz内仅有一阶由刀具模态主导的主模态，其模态频率误差为1.60%，对应负实部幅值误差为30.98%，同样具有较高的预测精度，进一步验证了本文预测模型的准确性。

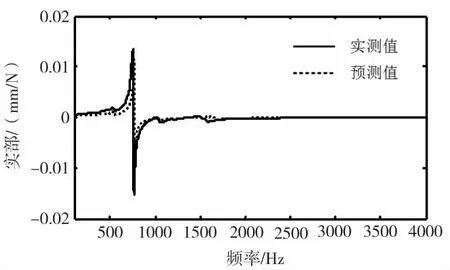
(a)实频特性曲线

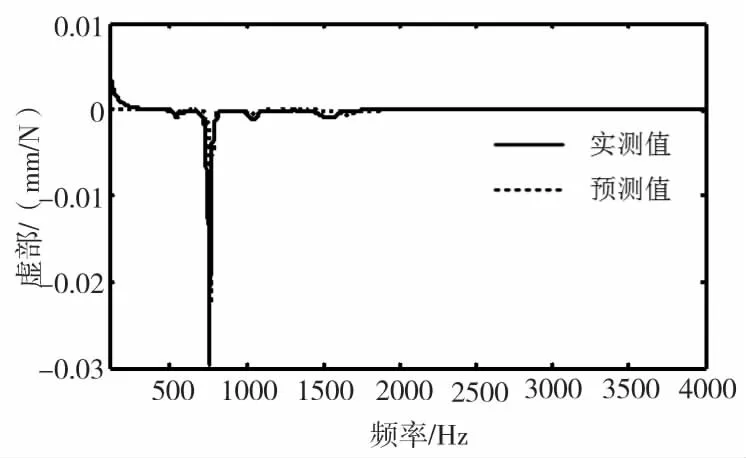
(b)虚频特性曲线图10 铣刀刀尖点预测与实测频响函数对比

4 结束语

基于RCSA法提出了一种主轴-刀柄-刀具系统刀尖点频响函数预测的方案，通过对主轴系统进行合理的子结构划分，简化了预测流程，提高了预测的效率。利用有限差分法、逆RCSA法等方法推导了子结构频响函数的获取算法，并通过实验间接获取子结构频响函数，进而快速准确地预测了刀尖点的频响函数，为高速铣削加工稳定性分析提供了可靠的基础。

[1] Schmitz T, Donaldson R. Predicting high-speed machining dynamics by substructures analysis[J]. Annals of CIRP, 2000, 49(1):303-308.

[2] Schmitz T, Duncan G. Three-component receptance coupling substructures analysis for tool point dynamics prediction[J]. Journal of Manufacturing Science and Engineering, 2005, 127(4): 781-790.

[3] Schmitz T, Powell K. Shrink fit tool holder connection stiffness/damping model for frequency response prediction in milling[J]. International Journal of Machine Tools & Manufacturing, 2007, 47(9): 1368-1380.

[4] Namazi M, Altintas Y. Modeling and identification of tool

holder-spindle interface dynamics[J]. International Journal of Machine Tools & Manufacturing, 2007, 47(9): 1333-1341.

[5] Hamid Ahmadian. Tool point dynamics prediction by three-component model utilizing distributed joint interfaces[J]. International Journal of Machine Tools & Manufacturing, 2010, 50(11): 998-1005.

[7] A Ertürk, H N özgüven, E Budak. Analytical modeling of spindle-tool dynamics on machine tools using Timoshenko beam model and receptance coupling for the prediction of tool point FRF[J]. International Journal of Machine Tools & Manufacturing, 2006, 46(15): 1901-1912.

[8] A Ertürk, H N özgüven, E Budak. Effect analysis of bearing and interface dynamics on tool point FRF for chatter stability in machine tools by using a new analytical model for spindle-tool assemblies[J]. International Journal of Machine Tools & Manufacturing, 2007, 47(1): 23-32.

[9] 闫蓉, 蔡飞飞, 彭芳瑜, 等. 基于响应耦合方法的铣刀刀尖点频响函数预测[J]. 华中科技大学学报: 自然科学版, 2013, 41(4): 1-5.

[10] 李孝茹, 朱坚民, 张统超, 等. 基于RCSA与GA的铣刀刀尖点频响函数预测[J]. 计算机集成制造系统, 2016, 22(1): 272-280.

[11] 王二化, 吴波, 胡友民，等. 主轴-刀柄与刀柄-刀具结合面参数辨识研究[J]. 振动与冲击, 2014, 33(10): 50-54.

[12] P Albertelli, M Goletti, M Monno. A new receptance coupling substructure analysis methodology to improve chatter free cutting conditions prediction[J]. International Journal of Machine Tools & Manufacturing, 2013, 72(3): 16-24.

ModelingofSpindleDynamicsandToolPointFrequencyResponseFunctionPrediction

LIU Cheng-ying1a,1b，LIU Wei1a,1b，ZHENG Feng2，ZHANG Zhi1a,1b，ZHANG Jie1a,1b

(1a.Department of Mechanical Engineering；b.Beijing Key Lab of Precision/Ultra-precision Manufacturing Equipment and Control, Tsinghua University, Beijing 100084,China;2. School of Mechatronics Engineering, University of Electronic Science and Technology of China, Chengdu 611731,China)

To obtain the tool point frequency response function (FRF) for constructing a stability Lobe diagram, a new spindle system model based on receptance coupling substructure analysis (RCSA) method was presented. Spindle-holder-tool assembly was divided into three substructures according to practical application: the spindle-holder base; the extended holder-tool holding part; and tool overhang part. And substructures′ frequency functions were obtained by impact test; finite difference method; inverse RCSA method and Timoshenko beam model. This method avoided the modeling and parameter identification of interface, which could predict tool point RFR with different holder-tool combination simply and accurately. Experiments were carried out on 170XDS20Z11 spindle system, the results showed a good agreement with prediction.

receptance coupling; frequency response function; substructure; prediction

1001-2265(2017)11-0011-05

10.13462/j.cnki.mmtamt.2017.11.004

2017-03-03；

2017-03-14

国家科技重大专项(2013ZX04001-021)

刘成颖(1960—)，女，辽宁大连人，清华大学副教授，研究方向为精密与超精密加工工艺及其装备、直线直驱技术与精密运动控制、智能检测与监控，(E-mail)liucy@tsinghua.edu.cn。

TH113;TG113.25

A

(编辑李秀敏)