基于子结构的柴油机曲轴有限元建模方法研究
张明明 赵建华 张瑞波(海军工程大学动力工程学院湖北武汉430000)
基于子结构的柴油机曲轴有限元建模方法研究
张明明赵建华张瑞波
(海军工程大学动力工程学院湖北武汉430000)
以某V6柴油机曲轴为研究对象,给出了两种划分曲轴子结构的方法,建立了曲轴的常规有限元模型和子结构有限元模型。模态分析表明子结构有限元模型与常规有限元模型振型一致,模态频率误差小于5%,加载10 kN的集中力后计算结果误差小于10%。因此,子结构建模方法适用于有较多重复几何特征的柴油机结构动力学分析。
子结构曲轴有限元模态分析
引言
柴油机是一个复杂的机械系统,建立一个切合实际的柴油机结构动力学模型是进行柴油机动力学分析的基础。然而,柴油机等大型复杂机械系统的有限元模型建模困难,求解需要消耗大量的计算资源和劳动成本。实际工程中经常需要对这些复杂构件的结构和动力学特性进行快速准确地分析计算或者预测。针对这一问题,可采用子结构建模分析技术对柴油机进行有限元分析,建立柴油机零部件子结构库,允许分析人员分享子结构,减少对柴油机重复部件的建模工作,实现单独运算,提高了效率。
曲轴是柴油机动力传递组件,也是力及强度分析的关键部件。曲轴的计算模型经历了从和曲拐的简支梁模型发展到后来的整根曲轴的连续梁模型和空间刚架模型,以及到目前的整体曲轴三维有限元模型。整体三维有限元连续体模型是最合理的模型,计算精度高[1-3]。为了更好更快地对多缸机进行结构动力学分析,本文尝试采用子结构分析方法,开展子结构建模与分析。
1 子结构法的基本理论
子结构的概念是有限元中一般单元概念的拓展,即将某一个结构的若干个基本单元缩聚在一起,组成一个新的超级结构单元,这个新的超级结构单元称为原结构的子结构或称为超级单元。
将一个大型的复杂结构划分为由若干个子结构和非子结构组成,先分别计算各子结构的刚度、质量矩阵和界面结点信息等,然后再将子结构与非子结构组装成整体结构,最后确定整体结构的刚度特性。这种结构分析的方法称为子结构分析法。
采用子结构分析法,可将大型问题化为若干各小问题,将大型问题的联立方程组分解为若干组小型的方程组,从而减小对计算机的要求,实现微机解大题的可能。也可以在求解整机响应的有限元模型中,减小不关注的零部件模型规模,或消除结构特别复杂、网格质量特别差的部件对求解可行性的影响。
子结构是一种超级单元,具有相当多的内部结点和自由度。在子结构与其他子结构或单元联结前,要将子结构内部自由度缩减,达到减少整个系统的总自由度的目的。
子结构分析方法中的动力方程[4]
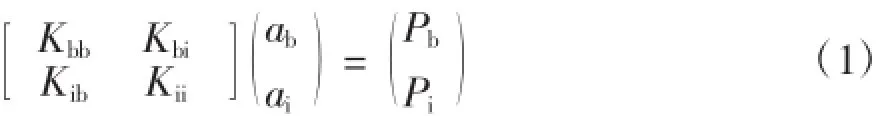
其中ab及ai分别是子结构交界面上结点的和内部结点的位移向量。
由(1)式的第二式可以得到

将式(2)代入式(1)的第一式,可以得到方程
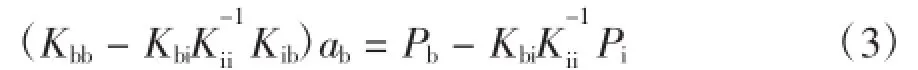
可以简单地写成如下的形式


由上面的论述,我们可以得知,只要计算出子结构保留结点的位移,子结构所有结点的位移和应力都可以根据Ka=P求解出[5]。由于缩聚后的子结构刚度矩阵的阶数b小于缩聚前的刚度矩阵K的阶数,组装缩聚后的各个子结构得到整体结构,整体结构的刚度矩阵的阶数就会成倍数地降低,所以应用子结构分析法在微型机上完成求解大型复杂结构的强度等问题有明显的优势。
2 基于子结构的曲轴有限元建模方法
2.1曲轴参数
图1所示为某V6型柴油机曲轴,该曲轴有3个单拐,各单拐在结构上相同(不考虑平衡块结构)。曲轴的材料为42CrMoA,弹性模量为E=2.10×105MPa,泊松比μ=0.3,密度ρ=7.8×10-9t/mm3。

图1 某柴油机曲轴
2.2曲轴子结构的划分
对结构进行建模时,首先必须要对结构的几何特征以及物理状态有清楚的了解,才能进一步划分子结构进行子结构分析。依据曲轴的结构特征,有两种子结构建模方式。
第一种,把整根曲轴离散化为若干个子结构。例如,可以把曲轴看成由3个单拐以及自由端和飞轮端组成的结构,因此曲轴可离散成为5个子结构。单拐、自由端、飞轮端的子结构如图2 a)、b)、c)所示。
第二种,对以上各子结构作进一步的离散,形成二层或多层子结构。例如,单拐可以进一步离散为2个半单拐,如图2 d)所示。

图2 曲轴用子结构方法逐级离散示意图
第一种方法整根曲轴CRANK调用SUP2、SUP3定义的超级单元各一次,调用SUP1定义的超级单元3次便可生成;第二种方法,单拐SUP1调用两个由SUP4定义的半单拐子结构,整根曲轴CRANK就是调用SUP2、SUP3定义的超级单元1次,调用SUP4定义的超级单元6次而生成。上述两种曲轴子结构构成可分别用图3和图4所示的结构构成树来表示。
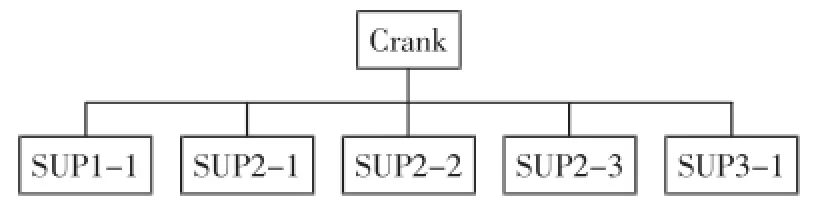
图3 曲轴单级子结构构成树

图4 曲轴多级子结构构成树
构成完整曲轴的所有子结构都可以在结构树里找到自己的位置,各子结构相互之间的关系非常直观,并为以后将计算结果扩展到子结构内部结点的应力求解分析提供方便。本文采用第一种方法,即单层子结构的方法,建立曲轴的子结构有限元模型。考虑到下一步子结构之间的组装要求,对各子结构划分网格时,相互连接的子结构界面上结点位置要对应一致。为方便建模可在Hypermesh中对子结构界面上的结点重新对应编号。
2.3各子结构特性分析
为了减小动力分析的误差,更好地表现整体模型的动态特性,需要提取子结构的模态信息。本文提取各子结构的前20阶模态。这里列出曲轴各子结构的前2阶振动模态和频率信息。
分析曲轴飞轮端子结构SUP1、SUP2、SUP3的各阶模态。表1是子结构的前2阶固有频率。图5是子结构的前2阶振型图。

表1 子结构自由状态固有频率Hz


图5 子结构振型图
2.4子结构装配
按照图3,调用SUP1、SUP3各1次,调用3次SUP2,组装成6缸机的完整曲轴,如图6所示。显然,按照这种方法还可以方便快速地完成8缸机、12缸机的曲轴有限元建模。结构越复杂,子结构法的优势越明显。

图6 曲轴子结构模型的子结构调用
曲轴的子结构有限元模型如图7所示。
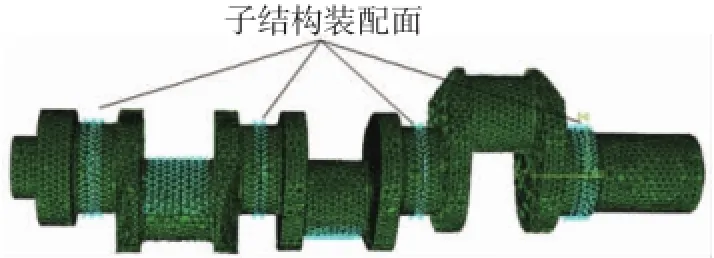
图7 曲轴子结构有限元模型
该曲轴子结构有限元模型共有5个单元,962个结点,对比曲轴常规有限元模型中的20 441个结点,95 776个单元,子结构有限元模型的规模大大缩减了。
3 子结构模型有效性分析
3.1模态对比分析
基于包含模态信息的子结构有限元模型,计算子结构组装后的曲轴各阶模态,模态计算结果及与常规有限元模型计算结果的对比如表2和图8所示。
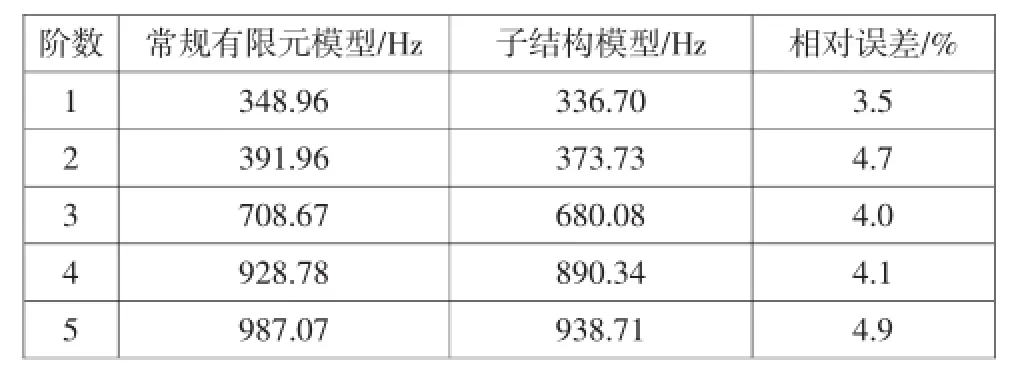
表2 常规有限元模型与子结构模型模态频率比较
通过模态频率和模态振型的比较可以发现,整体有限元模型和子结构有限元模型无论是从频率上看还是从振型上看,结果都吻合得比较好,模态频率误差小于5%。故可认为所建立的曲轴有限元模型是准确、合理的。

图8 常规有限元模型模态与子结构模型模态振型对比图
3.2静载荷计算对比分析
在曲轴常规有限元模型和子结构模型第二缸连杆轴颈的同一位置结点上加载10 kN的集中力,得到曲轴两种模型的应力分布,如图9所示。第一缸、第三缸曲轴曲柄销及曲柄臂的应力分布规律相同,两种模型考核节点应力计算结果误差小于10%。

图9 常规有限元模型模态与子结构模型结果对比图
4 结论
本文主要对某V6柴油机的曲轴进行子结构建模,提取各子结构的质量矩阵、刚度矩阵以及子结构模态频率,建立了该曲轴的子结构库,并生成了整根曲轴的子结构有限元模型。
子结构有限元模型的模态分析结果与常规有限元模型模态分析结果误差小于5%,两者的静力分析结果误差小于10%。因此对含有重复几何特征的部件,如柴油机曲轴、机体等,生成子结构库,分析时直接调用、复制,可节省生成整机模型的时间和精力。
1巨建民,吴昌华.柴油机曲轴整体三维强度分析[J].车用发动机,1996(5):32-35
2丁彦闯,牛天兰,吴昌华,等.柴油机曲轴整体三维应力精细分析[J].内燃机工程,1999(4):32-36,42
3S.Besset,L.Jézéquel.Dynamic substructuring based on a double modal analysis[J].Journal of Vibration and Acoustics,2008,130(1):107-116
4Suarez L E,Singh M P.Dynamic condensation method for structural eigen value analysis[J].AIAA,Journal,1992,30(4):1046-1054
5荀兵.子结构在有限元线静力分析中的应用[J].矿山机械,2003(02):48-50
Research on the Finite Element Modeling Method of the Crankshaft in Diesel Engine based on Substructure
Zhang Mingming,Zhao Jianhua,Zhang Ruibo
School of Power Engineering,Naval University of Engineering(Wuhan,Hubei,430000,China)
Taking the crankshaft of a V6 diesel engine for object,this paper gives two methods to divide the crankshaft into substructures,and establishes a conventional finite element model and a substructure model of a crankshaft.Modal analysis showed that the vibration modes of two finite element models,the error of modal frequencies was less than 5%and the calculation error was less than 10%when a 10KN concentrated force was loaded on the crankshaft.Therefore,the substructure modeling method is suitable for structure dynamic analysis of the diesel which contains more repeated geometric features.
Substructure,Crankshaft,Finite element,Modal analysis
TK423.3
A
2095-8234(2015)04-0027-06
2015-04-26)
张明明(1991-),男,硕士研究生,主要研究方向为热力系统设计、优化及仿真。

