磁流变弹性体减振单元动力学分析
王 磊,李长河,贾东洲,3,牛绍全
(1.福士汽车零部件(济南)有限公司,山东 济南 250000;2.青岛理工大学机械与汽车工程学院,山东 青岛 266520;3.内蒙古民族大学机械工程学院,内蒙古 通辽 028000)
1 引言
汽车在行驶中,会受到来自地面的激励振动。汽车系统激振主要来源有:因路面不平引起的系统低频随机振动、发动机引起的系统高频振动及车辆行驶加速、制动、转向过程中引起的振动[1]。其中,频率在(0.5~25)Hz之间的低频随机振动对车辆影响较大,而高频振动作为局部振动对整车影响较小[2]。减振系统可有效降低外部激励引起的低频振动,提高行驶平顺性。被动式减振器无法调和汽车运动性和舒适性之间的矛盾[3]。近年来磁流变液减振技术发展迅速,已成功应用于凯迪拉克等品牌汽车。新型减振器中的磁流变液具有粘度可控、响应迅速的特性,可依据通电状态主动改变磁流变液粘度,进而调控阻尼力[4]。但磁流变液减振器存在对中性差、密封要求高、铁磁质易沉淀等技术瓶颈。
文献[5]对比分析了三种磁流变弹性体(MRE)模型,结果表明挤压模式磁流变弹性体减振器具有最佳移频特性。文献[6-7]设计了一款磁流变弹性体减振器,通过动力学分析发现其具有吸振效果良好,刚度阻尼可控等优势。但这种基于剪切模式的磁流变弹性体减振器,无法应用于重载环境。
这里提出一种可用于重载环境的挤压模式磁流变弹性体减振单元,并利用等效模型和两自由度模型对其进行动力学特性和振动特性分析,分别得到一个振动周期内不同电流强度下的位移均方根值和加速度均方根值以及不同车速下均方根值,为控制系统的设计以及减振单元结构的布置提供了理论基础。
2 减振单元结构及动力学特性分析
2.1 减振单元结构
挤压模式下的磁流变弹性体减振单元为上下对称结构,上半部分,如图1 所示。主要由铁芯、缸筒、气隙、导磁板、磁流变弹性体等部分构成,其中缓冲气囊与活塞单元不参与磁路循环。由于磁流变弹性体刚度较大,为了避免结构硬冲击,将磁流变弹性体和缓冲气囊串联增强缓冲[8]。磁流变弹性体和缓冲气囊均具有变刚度特性,因此由两者组成的减振系统近于理想弹性特性,即在不同载荷之下能够保持固有频率保持不变,且变形挠度较小。
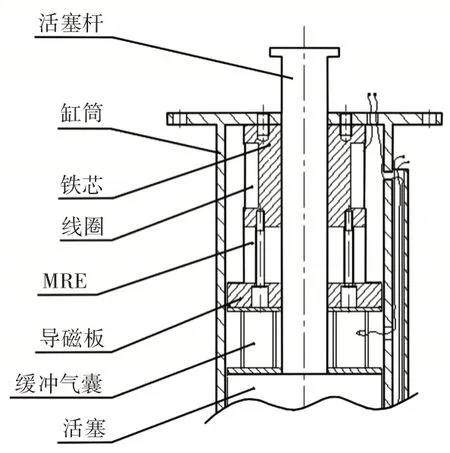
图1 磁流变弹性体减振单元结构Fig.1 The Damping Unit Structure of Magnetorheological Elastomer
2.2 减振单元等效模型及弹性特性
车辆偏频fn通常由车身质量和刚度决定,是设计减振单元的重要性能指标,可按式(1)计算。车辆偏频应避开(4~8)Hz的人体敏感频率,一般舒适偏频取值为(1~1.6)Hz。

式中:fn—车辆偏频(Hz);
k—悬架刚度(N/m);
m—系统质量(kg)。
将车辆偏频和系统质量(单个减振单元承重500kg)代入式(1)可以得到减振单元的系统刚度为(19.7~50)N/mm。
减振单元一般包括弹簧部分及阻尼部分,弹簧用于吸收振动能量,阻尼器用于能量消耗转化。这里方案等效模型,如图2所示。减振单元上半部分磁流变弹性体(MRE)的弹性系数为k1,缓冲气囊的弹性系数为k2,可将其等效成刚度系数为keq1的弹簧Ⅰ;下半部分缓冲气囊的弹性系数为k3,磁流变弹性体的弹性系数为k4,可将其等效成刚度系数为keq2的弹簧Ⅱ,c1和c2分别为压缩阻尼和伸张阻尼。

图2 振动系统等效模型Fig.2 The Equivalent Model of Vibration System
磁流变弹性体和缓冲气囊的静变形之和与等效弹簧的静变形相等,若其静变形分别为δs1和δs2,则等效弹簧的静变形δseq为:

式中:δs1—磁流变弹性体的静变形(mm);
δs2—缓冲气囊的静变形(mm);
δseq—等效弹簧的静变形(mm)。
依据胡克定律则有:

即:

2.3 阻尼特性
传统被动式减振单元阻尼通常为伸张阻尼比较大而压缩阻尼小,若要获得较大承载能力,只能提高弹簧刚度值,但是由于弹簧为蓄能元件,易产生强烈反弹。双向可变阻尼可迅速衰减振动,能够有效保护机械构件。弹簧-质量-阻尼系统振动衰减快慢程度通常用相对阻尼比ζ评价。根据振动理论和工程设计经验[10],垂直安装减振单元,悬架阻尼可由下式确定:

式中:ζ—悬架系统阻尼比(无量纲);
C—等效阻尼系数(N(/m/s));
K—悬架刚度(N/m);
m—悬架质量(kg)。
磁流变弹性体减振单元通过改变电流值大小改变磁场强度,进而控制磁流变弹性体阻尼。按照最小系统刚度K=19.7N/mm配置上部缓冲气囊,选择最小阻尼比ζ为0.22,定义质量为500kg,可得初始压缩等效阻尼系数C为1.4N(/mm/s)。初始伸张等效阻尼系数选为2.0N(/mm/s),根据式(5)可得下部缓冲气囊刚度为40N/mm。
3 磁流变弹性体减振单元振动特性分析
3.1 两自由度模型
汽车行驶中路况不平度存在随机性,所以振动输入激励也存在随机性。在随机激励下,汽车的车轮、车架和车身均会产生振动,导致汽车振动分析极为复杂,这里磁流变弹性体减振单元的减振分析仅考虑垂直方向振动。
若振动系统满足以下假设条件,汽车振动系统就可简化为车身垂直方向两自由度振动系统[11]。
(1)受到路面不平激励时,由于轮胎阻尼远远小于减振单元阻尼,只考虑轮胎的刚度作用,忽略其阻尼效果;(2)假设汽车结构及质量分布对称,且路面对汽车两侧轮胎激励相同,可将汽车振动简化为一个平面内的振动问题;(3)假设车架、车身的刚度足够大,不考虑车架弹性引起的各阶振动;(4)将乘员视为车身系统。
基于上述假设,建立图1/4单轮车辆模型,如图3所示。该模型为两自由度车辆振动系统简化模型,根据牛顿第二定律,可以得到系统的运动学方程。

图3 1/4单轮车辆模型Fig.3 A Quarter of a Single Wheel Vehicle Model
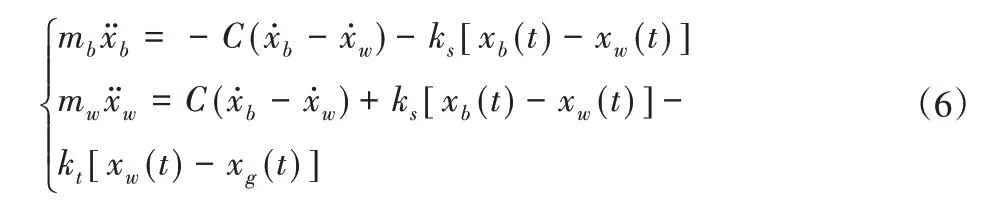
式中:xg—路面位移(mm);
xb—车身位移(mm);
xw—车轮位移(mm);
mb—车身质量(kg);
mw—车轮质量(kg);
Ks—悬架弹簧刚度(N/mm);
Kt—轮胎刚度(N/mm);
C—悬架阻尼(N(/mm/s)))。
基于上述理论模型,采用虚拟样机技术ADAMS 仿真分析,可模拟磁流变弹性体减振单元对实际路面的激励响应。
3.2 模型及参数
在ADAMS/View中建立磁流变弹性体减振系统1/4单轮仿真模型,如图4所示。施加约束后进行振动分析,利用均方根值评价法对减振前后的振动输出信号进行评判。模型振动分析具体边界条件可确定如下。
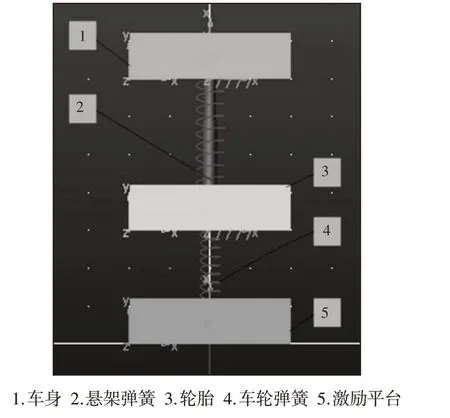
图4 Adams中磁流变弹性体减振单元的仿真模型Fig.4 The Magnetorheological Elastomer Damper Simulation Model in Adams
3.2.1 路面随机激励信号
建立B级路面下的随机激励信号,以接近实际行车情况。白噪声法具有计算速度快、精确等优点,因此采用白噪声法建立时域模型[12]。利用Matlab/Simulink 搭建模型,输入速度40km/h和路面不平度系数,即可得到所需要的时域响应输出,如图5 所示。将曲线导入Adams 生成Spline,作为Adams/Vibration 仿真的激励输入。

图5 Matlab/Simulink中路面谱时域输出信号Fig.5 The Road Surface Spectrum Output Signal in Matlab/Simulink
3.2.2 其它边界条件设定
1/4 车身质量mb=500kg,轮胎质量mw=40kg,悬架初始阻尼系数C=1.4N(/mm/s),轮胎的刚度Kt=2.2N/mm,悬架弹簧刚度Ks=1.97N/mm。
磁场强度和电流强度成正比例关系,由欧姆定律以及磁路分析得知在电流为2A 时,磁流变弹性体的磁场强度能够达到0.7095T[13],进而可得各磁场强度下相应的电流值。
磁流变弹性体作为一种磁滞粘弹性材料,可以通过循环加载力实验得到磁滞环,能够得到在不同磁感应强度时的磁致压缩模量E,由式(7)进而得到不同磁场强度下的等效刚度Kc和阻尼[14],如表1、表2所示。

表1 压缩状态时不同磁感应强度下的各参数值Tab.1 The Each Parameter Value Under Different Magnetic Induction Intensity in the State of Compress Condition
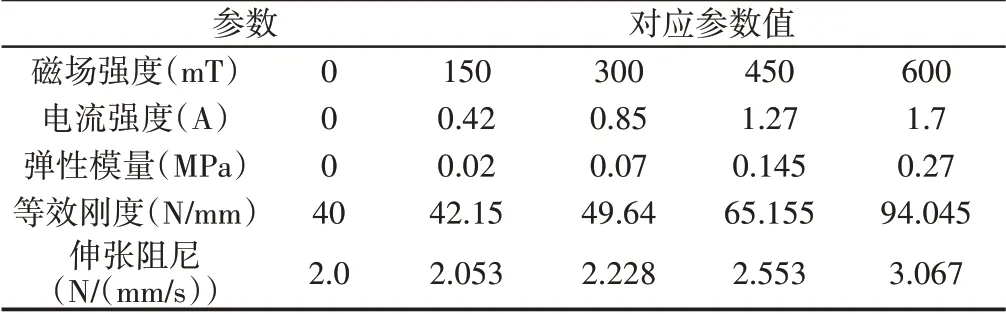
表2 伸张状态时不同磁感应强度下的各参数值Tab.2 The Each Parameter Value Under Different Magnetic Induction Intensity in the State of Stretched Condition

式中:E—磁致压缩模量(MPa);
A—磁流变弹性体截面积(mm2);
h—磁流变弹性体的高度(mm)。
3.3 不同磁场下均方根值分析
将上述参数分别输入到Adams/Post processor,能够得到5种磁场压缩状态车身垂直方向位移曲线和振动加速度曲线,在Ad⁃ams中进行FFT变化,在频率(0~50)Hz之间进行数据处理,统计得各参数的均方根值,如表3所示,随着磁场强度的增加,车身加速度和车身位移均降低。

表3 压缩状态各参数值的均方根值Tab.3 The Root Mean Square Value of Parameter Value in the Compression State
将压缩状态下的数据重新生成Spline,导入Adams重新加载振动,得到伸张状态下的车身位移曲线和车身垂向振动加速度曲线。经统计可得各参数的均方根值,如表4所示。

表4 伸张状态各参数值的均方根值Tab.4 The Root Mean Square Value of Parameter Value in the Stretching State
进一步分析压缩状态下和伸张状态的车身位移和加权加速度均方根值。减振单元在一个振动周期内压缩状态和伸张状态的位移均方根值,如图6所示。可知减振单元在压缩状态下,位移衰减并不明显,在伸张状态时可快速衰减位移。因此可以在满足减振效果的同时设计合理的悬架所需要的行程空间。磁场强度在(300~450)mT之间时,位移均方根值可迅速衰减到13mm;磁场强度在(450~600)mT 之间时,位移均方根值可迅速衰减到7.5mm,这为控制系统设计及减振单元结构布置提供了理论基础。一个振动周期内压缩状态和伸张状态的加权加速度均方根值,如图7所示。在压缩状态下,当磁场强度在(300~450)mT之间时,加权加速度均方根值衰减比较迅速;在伸张状态下,当磁场强度在(450~600)mT之间时,衰减比较迅速,因此在控制系统设计时应该控制电流迅速产生相应磁场。完成一个周期后,加权加速度均方根值衰减到270mm/s2。

图6 压缩状态和伸张状态下位移均方根值曲线Fig.6 The Graph of Displacement Root Mean Square Value Under Compression and Stretching State

图7 压缩状态和伸张状态下加速度均方根值Fig.7 The Graph of Accelerate Root Mean Square Value Under Compression and Stretching State
3.4 不同车速下均方根值分析
进一步的分析车速度为20km/h、40km/h、60km/h、80km/h 和100km/h时车身加速度和位移。车辆在B级路面行驶,在不同电流状态下,压缩状态和伸张状态的加速度均方根和位移均方根随速度的变化趋势基本是相同的,如图8、图9所示。车辆行驶的速度对位移均方根值和加速度均方根值影响很大,在低速段(20~60)km/h,随着车速的增加车身位移和加速度均方根值随之增大,且增幅较大,因此降低了乘坐舒适性和操控稳定性。而在高速段(60~100)km/h加速度均方根值则会有所降低,其原因是在高速段,随着车速增加激振频率增加,车辆的振动趋势被路面抵消;在此速度段,位移均方根值继续增加,但是增长速度降低。由于加速度均方根值是人体舒适性的重要指标,因此应该以加速度均方根作为标准,牺牲减振单元动挠度来保证加速度的均方根值符合舒适标准,动挠度的增加可以通过设计充足的行程来满足。从图8(a)和图8(b)中可知在(60~100)km/h 速度段,施加电流为1.27A-1.7A(450-600)mT时加速度均方根值衰减较为迅速。从图9(a)和图9(b)可知,在(40~80)km/h速度段,施加电流为1.7A(600mT)时加速度均方根值衰减较为迅速;但位移均方根值在(20~100)Km/h速度段,施加电流为1.27A-1.7A(450-600)mT时衰减较为迅速。

图8 压缩状态下均方根随速度变化趋势Fig.8 The Root Mean Square Velocity Change Trend Under Compression State

图9 伸张状态下均方根随速度变化趋势Fig.9 The Root Mean Square Velocity Change Trend Under Stretching State
4 结论
(1)设计挤压模式的磁流变弹性体减振单元结构,确定加装气囊缓冲结构并分析其弹性特性及阻尼特性,得到系统刚度;
(2)将汽车比较复杂振动系统简化为车身垂直方向两自由度振动系统,并建立随机激励下的两自由度模型;
(3)建立B级路面随机输入信号,仿真得到不同电流源强度下车身位移和加速度曲线,结果表明:在外加电流下,车身位移和加速度迅速衰减。进一步得到了一个振动周期内不同磁场强度下位移均方根值和加速度均方根值。
(4)仿真得到不同车速下的均方根值,可知在五种电流强度下,压缩状态和伸张状态下加速度及位移均方根随速度的变化趋势基本相同。压缩状态下在(60~100)km/h速度段,电流为1.27A-1.7A(450-600)mT 时加速度均方根值衰减迅速;伸张状态下在(40~80)km/h速度段,施加电流为1.7A(600mT)时加速度均方根值衰减迅速;位移均方根值在(20~100)km/h的速度段,施加电流强度1.27A-1.7A(450-600mT)衰减比较迅速。

