基于Kriging模型与NSGA-II算法的堆垛机结构优化设计

杨瑞刚，高 林，董 青，徐格宁

（太原科技大学机械工程学院，山西 太原 030024）

1 引言

随着物流仓储的快速发展，巷道式堆垛机应时代而生，巷道式堆垛机作为物流仓储的专用堆垛机，是物流仓储中最要的搬运设备。随着用地面积的紧张，堆垛机正向高速度和大高度方向发展，这对堆垛机的设计提出更高的要求，针对国内的堆垛机性能指标落后，结构不合理、笨重等特点［1］，提出了对现有堆垛机结构在满足结构强度、刚度、稳定性条件下的快速优化设计。

双高双立柱式堆垛机在启动，加速运行，停止时，堆垛机金属结构受到各种载荷作用，易发生挠曲变形，产生局部应力集中［2］，故对堆垛机结构优化就显得异常重要。文献［2］通过运用参数化建模运用ANSYS求解，以立柱顶部挠度和立柱根部应力为优化目标，通过改变单个设计参数寻优，具有一定局限性，容易陷入局部最优。文献［1］通过运用MOGA遗传算法对单立柱堆垛机设置不同的约束条件进行静态优化。但由于设计参数较少，当设计参数关系复杂时，对其进行直接优化，工作量巨大，效率极低。而代理模型可以减少调用真实模型次数，提高优化效率，文献［3］运用Kriging模型和稳健性设计相结合对乘务员约束系统进行稳健性设计，提高了设计质量。文献［4］通过kriging模型和遗传算法对泵叶轮进行了尺寸优化，优化后效率提高5.53%。文献［5］通过Krig⁃ing模型和模拟退火粒子群算法对桁架模型进行了模型修正和损伤识别等验证。文献［6］将Kriging模型与传统优化算法和遗传算法进行对比，确定Kriging模型的有效性。并对翼型进行优化，翼型升阻比提高了81%，优化效果明显。文献［7］通过将代理模型应用到飞机旋翼上进行优化设计。文献［8］通过运用Kriging模型可以对非线性模型有很好的逼近能力。Kriging广泛应用于工程结构和飞行器多学科优化中，但将Kriging模型用于堆垛机整机优化还很少。

鉴于此，这里提出一种适合双高（速度高与高度高）堆垛机结构特点的方案，即基于Kriging 模型与非支配排序遗传算法（NSGA-II）的相结合的优化方法，将双高双立柱堆垛机的位移和质量作为待优化目标，综合考虑双高双立柱整机的约束情况，采用参数化三维建模，通过最佳填充样本空间（OSF）进行试验设计，考虑不同设计参数进行组合，避免陷入单个设计参数局部最优。通过试验设计构建克里金代理模型代替有限元模型（真实模型），可以最大程度避免在进行优化时调用真实模型次数，提高了优化效率。最后通过精英保留策略快速非支配排序多目标遗传（NSGA-II）算法对Kriging代理模型寻找全局最优Pareto解。

2 双高双立柱式堆垛机优化设计流程

由于双高双立柱式堆垛机结构是一个非线性问题，对其进行直接优化设计，将不断调用真实模型进行寻优，将大大降低了优化效率，为了解决此类优化设计问题，通过构造代理模型将成为关键。针对双高双立柱式堆垛机的特性，故需要找到一个精度高和能描述高度非线性过程的代理模型，文献［3］中指出通过构造Kriging 构造代理模型不仅可以描述高度非线性过程，还可以去除噪声。被广泛应用于高度非线性问题。

基于Kriging模型的双高双立柱式堆垛机静态多目标优化设计流程，如图1所示。

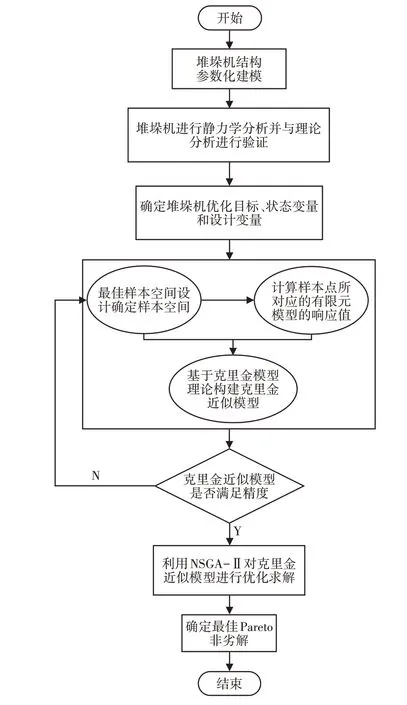
图1 堆垛机结构优化整体流程图Fig.1 Overall Flowchart of Stacker Structure Optimization

具体过程如下：

（1）对双高双立柱式堆垛机进行理论分析并通过构建有限元模型进行验证，确保优化设计模型的正确性；

（2）基于最佳样本空间（OSF）的试验设计方法和Kriging理论建立代理模型；

（3）通过NSGA-II 多目标优化算法对Kriging 代理模型进行求解，获得多个Pareto非劣解集；

（4）通过评价准则确定最佳Pareto非劣解。

3 双高双立柱堆垛机结构静力学分析

这里研究对象为双高双立柱式堆垛机，其基本参数，如表1所示。双高双立柱式堆垛机模型图，如图2所示。

表1 堆垛机基本参数Tab.1 Stacker Basic Parameters

图2 堆垛机模型Fig.2 Stacker Model

其中为主立柱、辅立柱、上横梁、下横梁各截面形式，如图3所示。其中L1为主立柱下端腹板长度，T1为主立柱下端翼板厚度，其中L2为主立柱上端腹板长度，T2为主立柱上端翼板厚度，T3为辅立柱腹板厚度，T4为辅立柱翼板厚度，T5为上横梁腹板厚度，T4为上横梁翼板厚度，T7为下横梁腹板厚度，T8为下横梁翼板厚度。

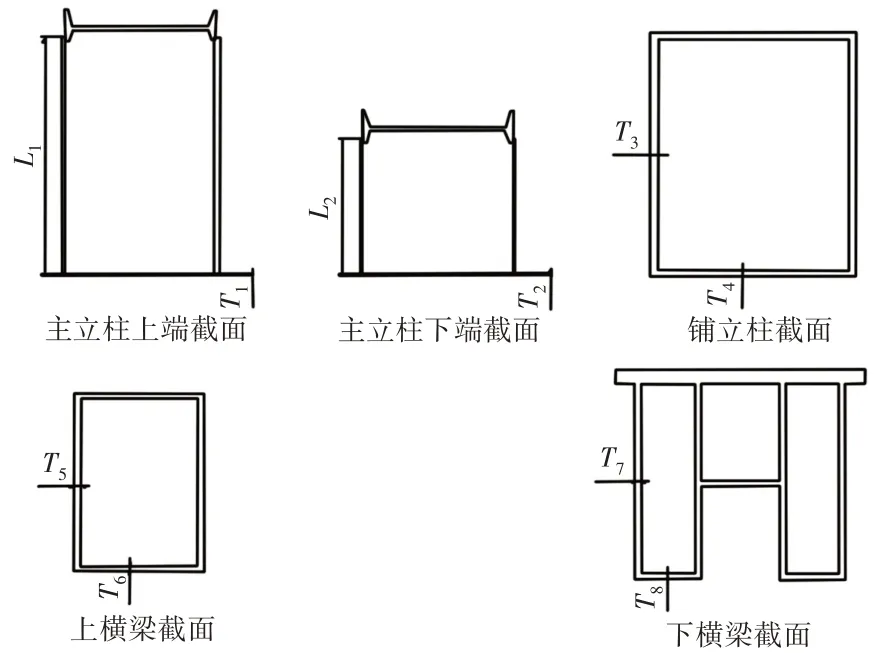
图3 各截面形式Fig.3 Each Section Form

3.1 堆垛机力学模型与有限元模型

当双高双立柱式堆垛机载货台运行到最高位置时，货叉全伸叉取满载货物。为最危险工况［9］，其堆垛机门架受力示意图，如图4所示。堆垛机门架结构力学模型，如图5所示。

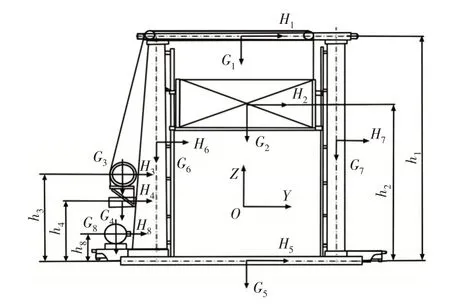
图4 堆垛机门架受力示意图Fig.4 Stacking Machine Frame Force Diagram

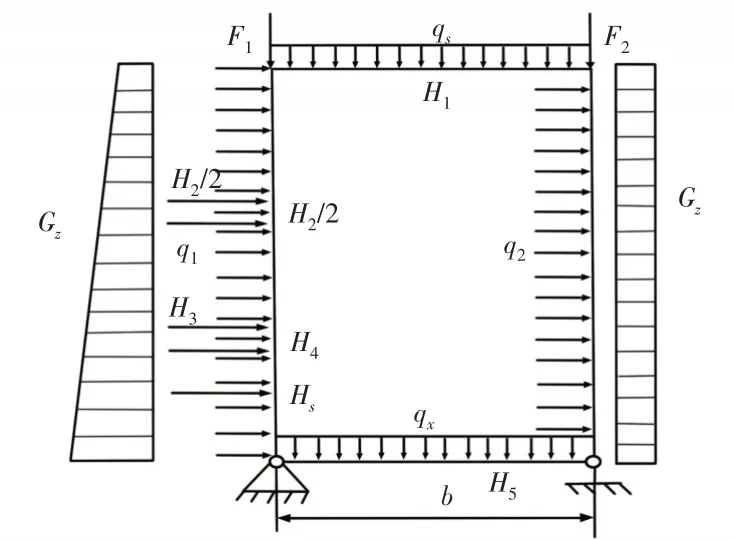
图5 堆垛机门架结构力学模型Fig.5 Mechanical Model of Door Frame Structure of Stacker

其中，自重载荷为：G1为上横梁及附件重力，G2为载货台、货物、司机室及附件的重力，G3为起升装置的重力，G4为电气控制柜的重力，G5为下横梁及附件重力，G6、G7为立柱重力，G8为运行机构自重，GZ1和GZ2分别为主立柱和辅立柱单位长度平均重力，qs和qx分别为上、下横梁单位长度平均重力，而h1～h5和h8分别对应于G1～G5和G8分别到下横梁中心线的质心高度。堆垛机在加速或者减速行走时产生的水平力为：H1～H5和H8对应于G1～G5和G8的水平惯性力，q1、q2分别为立柱的单位长度平均质量产生的水平惯性力。F1和F2分别为主立柱和辅立柱顶部作用力。

根据双高双立柱式堆垛机的工作特点、不同工况、考虑各项载荷实际出现的机率，按对结构最不利的作用情况，将可能同时出现的载荷分别按A1和A4进行组合，通过对比得到合理的载荷组合［10］。

按A1进行载荷组合时，取ϕ1=1.1，起升动载系数ϕ2按下式计算：

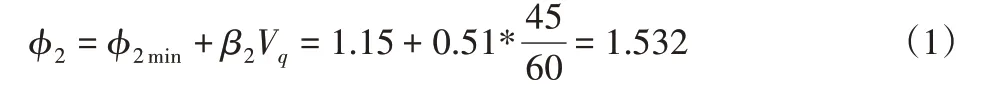
式中：ϕ2min—与起升状态级别相对应的起升动载系数的最小值；

β2—按起升状态级别设定的系数；

Vq—稳定（额定）起升速度，单位为m/s。

载荷组合A1下的总轮压：

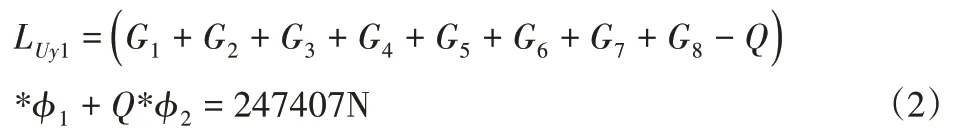
按A4进行载荷组合时运行冲击系数按式计算：

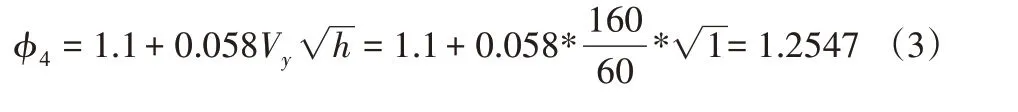
载荷组合A4下的总轮压：

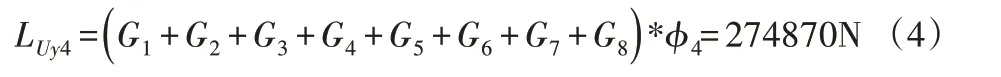
由于LUy4>LUy1因此因按载荷组合A4进行计算。

3.2 双高双立柱堆垛机有限元模型

双高双立柱式堆垛机的金属结构主要有，主立柱（变截面），辅立柱，上横梁，下横梁组成。建立双高双立柱式堆垛机的有限元的模型时要简化实际模型的中的一些不重要部件，使建立的有限元模型既可以反应实际模型的真实状况，又可以得到较为精确的结果。

双高双立柱式堆垛机的模型采用Solid works参数化建模，导入ANSYS workbench中，其中单元采用solid45单元，因为实体单元可以更好的模拟实际情况。主立柱，辅立柱，上横梁，下横梁之间均采用ANSYS workbench中的bonded接触。采用自由网格划分，建立有限元模型。其单元总数为17597，节点总数为109516，如图6所示。

图6 有限元模型Fig.6 Finite Element Model

根据双高双立柱式堆垛机的实际工作情况，在下横梁底部两端面与上横梁两侧面施加面约束，约束类型为：在A面施加固定约束，约束X，Y，Z三个方向自由度，在B面施加位移约束，限制住Y方向和Z方向的自由度，释放掉X方向的自由度。在C面和D面施加位移约束，限制Z方向的自由度，防止堆垛机前后摆动，使其始终保为平面，释放掉X和Y方向自由度。将堆垛机力学模型上面的力等效施加到有限元模型上，如图7所示。

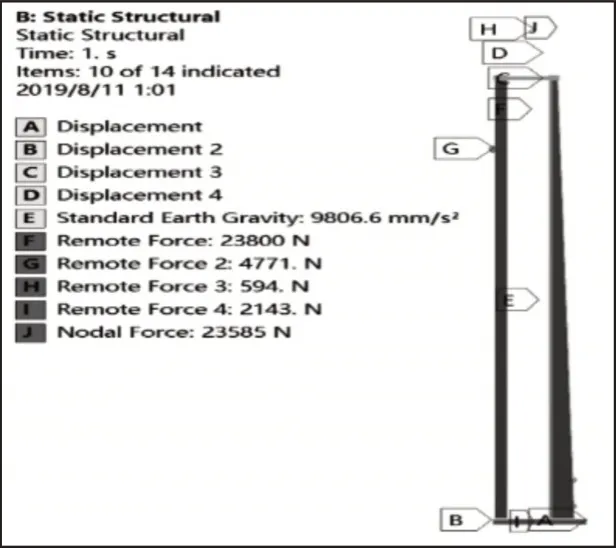
图7 载荷施加Fig.7 Load Application

3.3 有限元求解

通过云图9可知，在载货台移动到最高位置，且满载货物货叉伸出时的工况下，最大等效应力位移辅立柱下端，应力值为103.21MPa，且整个堆垛机金属结构在x方向产生的位移为41.157mm，小于许用位移值。由于堆垛机主立柱材料采用Q345，许用应力为[σ]=0.5*σs+0.35*σb ni=227MPa ，辅立柱材料采用Q235，许用应力为158MPa，由云图9可知，应力均小于许用应力。

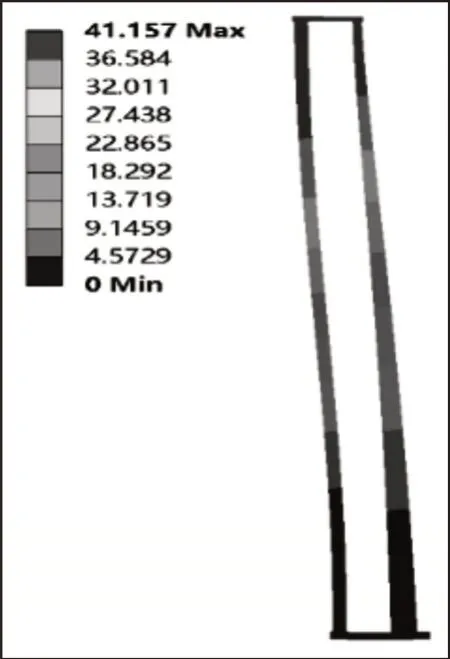
图8 堆垛机位移云图Fig.8 Stacker Displacement Cloud Diagram

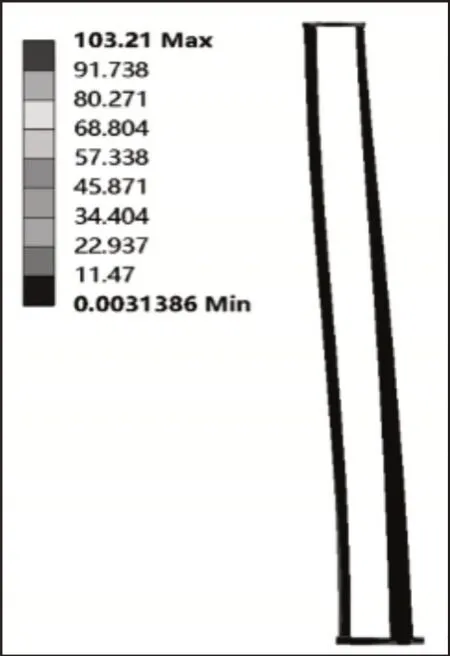
图9 堆垛机应力云图Fig.9 Stacker Stress Cloud Diagram

4 Kriging代理模型构建

由于双高双立柱式堆垛机在结构分析时为非线性过程，而Kriging 模型可以很好的描述非线性过程，同时也能光滑目标响应、去除噪声和提高优化设计效率［3］。Kriging模型的主要是有线性回归部分和随机分布部分所组成［11］，其样本点X=[x1，x2，x3…xn]T和响应值Y=[y1，y2，y3…yn]T，其中，样本点和响应点通过试验设计法中的最佳空间填充（OSF）来获得。其Krig⁃ing模型的数学表达式为：

式中：Y(x)—未知Kriging 模型；fi(x)—样本点的多项式回归组合，提供了设计空间的全局近似模拟；βi—回归系数的最小二乘估计；z(x)—从正态分布的随机项，是在全局近似模拟的基础上创建的局部偏差，其协方差方程表达式为：

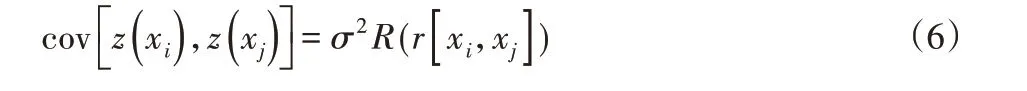
式中：R—N*N的协方差矩阵，沿对角线正定；r[xi，xj]—任意N个样本点中xi和xj空间函数相关，为高斯的相关函数：

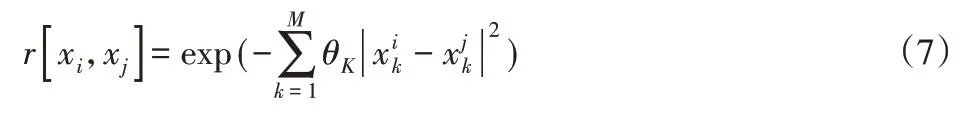
式中：θK—用于拟合模型的不确定参数；M—设计参数的数量。

通过确定相关函数，则样本点x处的响应估计为：

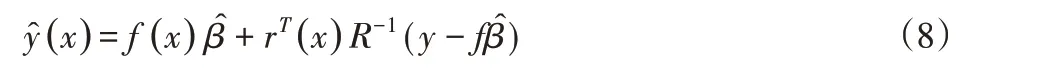
式中：y—样本点数据的响应值所组成的列向量；f—单位列矢量；

rT(x)—样本点和预测点之间得相关矢量，如式（9）所示：

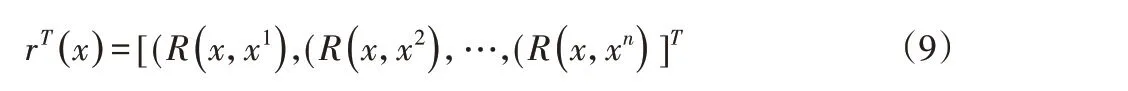
其中式（8）中β估计和式（6）全局模型方差估计值σ2如下式所示：

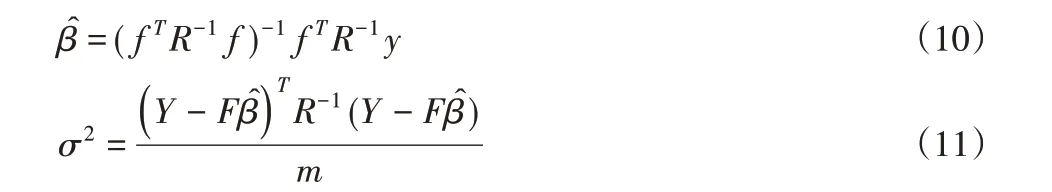
通过最大似然估计求解相关参数θK得到：

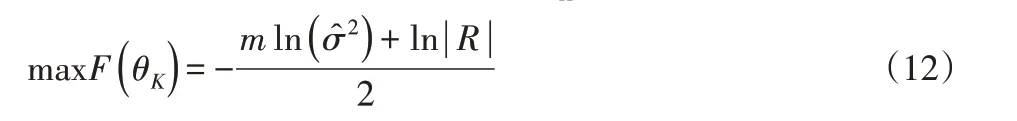
通过式（12）求解出θK后，可得到Kriging拟合精度最优的代理模型。

由于双高双立柱式堆垛机为非线性问题，因此在构建Krig⁃ing代理模型时，试验点的选取就显得异常重要。这里通过采用最佳填充空间（OSF）设计得到试验设计方法，最佳填充样本空间（OSF）相对于中心复合设计（CCD）可在整个设计空间均匀的分配设计参数，以最小的数量获得对设计点的最大洞察。根据设计点各个参数的取值范围，生成85组的样本点，进行计算，通过最佳填充空间（OSF）得到的样本点和响应值带入Kriging模型中构建响应面模型。通过拟合优度散点图可以观测Kriging模型拟合出的响应面精度好坏，其中，样本点越接近对角线，则表示Kriging模型拟合出的响应面精度越高，如图10所示。

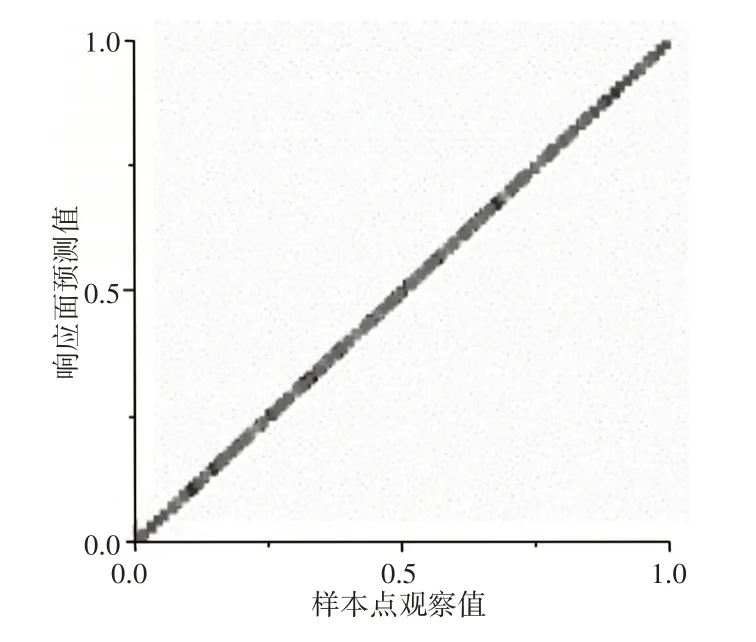
图10 拟合优度散点图Fig.10 Goodness of Fit Scatter Plot

设计参数与响应值通过Kriging模型拟合出的响应面图，如图11～图13所示。可以通过对不同的设计参数进行组合，得到设计参数与响应值不同的响应面图。通过响应面图还可以看出各个设计参数对响应值之间得影响。

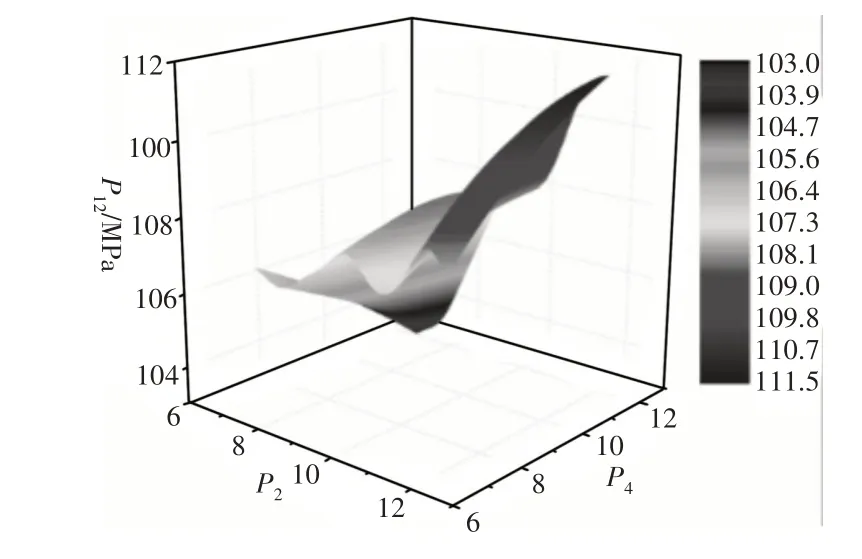
图11 设计参数与应力的拟合响应面Fig.11 Fitting Response Surface of Design Parameters and Stress

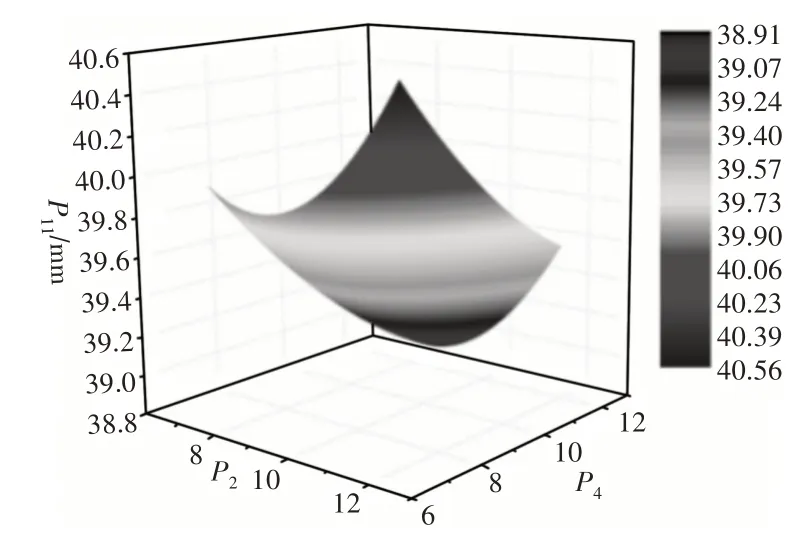
图12 设计参数与位移的拟合响应面图Fig.12 Fitting Response Surface of Design Parameters and Displacement

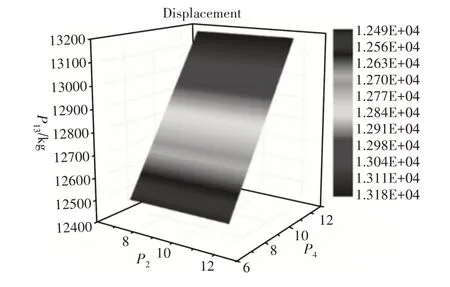
图13 设计参数与质量的拟合响应面图Fig.13 Fitting Response Surface of Design Parameters and Mass

5 堆垛机结构多目标优化数学模型

基于双高双立柱堆垛机金属结构模型，建立以主立柱下端腹板长度L1、主立柱下端翼板厚度T1、主立柱上端腹板长度L2、主立柱上端翼板厚度、T2辅立柱腹板厚度T3、辅立柱翼板厚度T4、上横梁腹板厚度T5、上横梁翼板厚度T4、下横梁腹板厚度T7、下横梁翼板厚度T8为设计参数，堆垛机结构强度为约束条件，堆垛机结构刚度和质量为优化目标的多目标数学优化模型如下所示：

式中：m—堆垛机结构质量；y—堆垛机结构最大位移；σmax—堆垛机结构最大应力值；[σ]—钢材许用值；xi—设计参数。

5.1 优化算法

多目标遗传算法（NSGA-II）是通过精英保留策略快速非支配排序的算法，是一种基本Pareto最优解集的多目标算法［13-14］。其分析流程图，如图14所示。其具体步骤为：（1）在变量范围内随机生成初始化种群，根据Pareto 的等级关系对生成的种群进行非支配排序后，带入遗传算法中进行选择、交叉、变异后，生成第一代子代种群。（2）第二代开始，将父代与子代合并，并进行非支配排序，同时对非支配关系层中的个体进行拥挤度计算，使解在目标空间更加均匀。根据个体拥挤度和非支配关系选择合适的种群组成新的父代种群，然后在带入遗传算法进行选择、交叉、变异生成新的子代种群。循环进行，直到满足进化代数要求［15］。

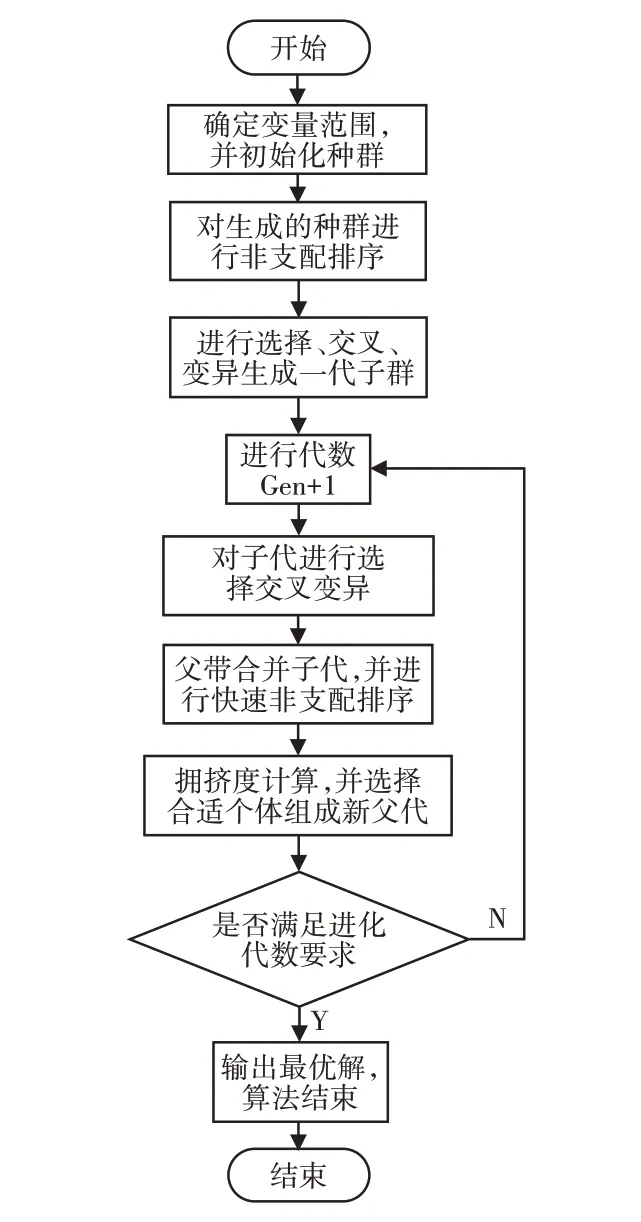
图14 NSGA-II算法流程图Fig.14 NSGA-II Algorithm Flowchart

5.2 模型优化对比

由于双高双立柱式堆垛机有限元模型单元数量众多，为了提高双高双立柱式堆垛机的优化效率。分别采用NSGA-II多目标优化算法对堆垛机有限元模型进行优化和基于最佳样本空间（OSF）试验设计构建的Kriging代理模型进行优化对比，由于直接优化与初始种群规模有直接影响，为了减少仿真时间，NSGA-II参数设置：初始种群规模为100，最大允许的Pareto 百分比为70%，进化代数50，突变因子概率为0.02，交叉因子概率为0.98。其对比结果，如表2所示。

表2 不同模型的优化对比Tab.2 Comparison of Model Optimization

通过表2 表明：基于最佳样本空间（OSF）试验设计构建的Kriging 代理模型进行优化相对于NSGA-II 对真实模型优化调用次数较少65次，优化时间减少了12.992h，优化效率提升明显。NSGA-II 多目标优化算法对参数进行设置［13］，初始种群规模为300，最大允许的Pareto百分比为70%，进化代数300，突变因子概率为0.02，交叉因子概率为0.98。通过对Kriging拟合代理模型进行自适应多目标优化，得到的为Pareto解非支配排序散点图，如图15所示。

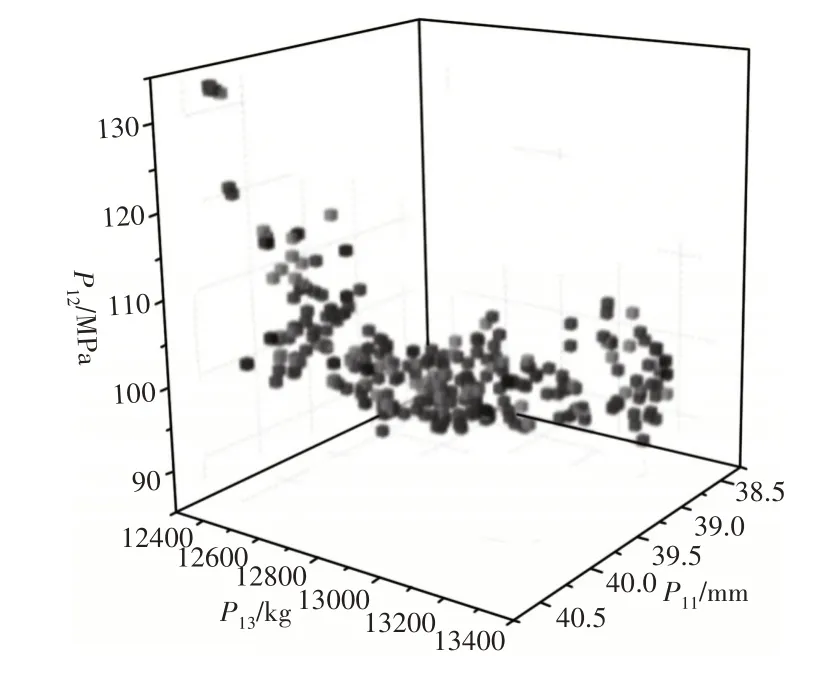
图15 Pareto解集散点图Fig.15 Pareto Solution Scatter Plot

通过在Pareto非支配排序最优解集中选出5个优化设计方案中，通过对其圆整后，如表2所示。

由表3可知在Pareto最优解集中的5个优化设计方案中可以看出目标函数δmax，σmax，与mass之间存在某种制约关系，因而选择出一个折中方案。方案1 相对于剩余方案质量较少了（5.4～8.7）%，而方案一的应力和位移相对于其他方案相差不大，因此选择方案1作为堆垛机多目标优化的最优解。通过表四最优解与初始解进行对比可知，其堆垛机整机质量下降了5%，最大位移减小了2.7%，最大应力增加了14%，却依然满足静强度和静刚度要求。

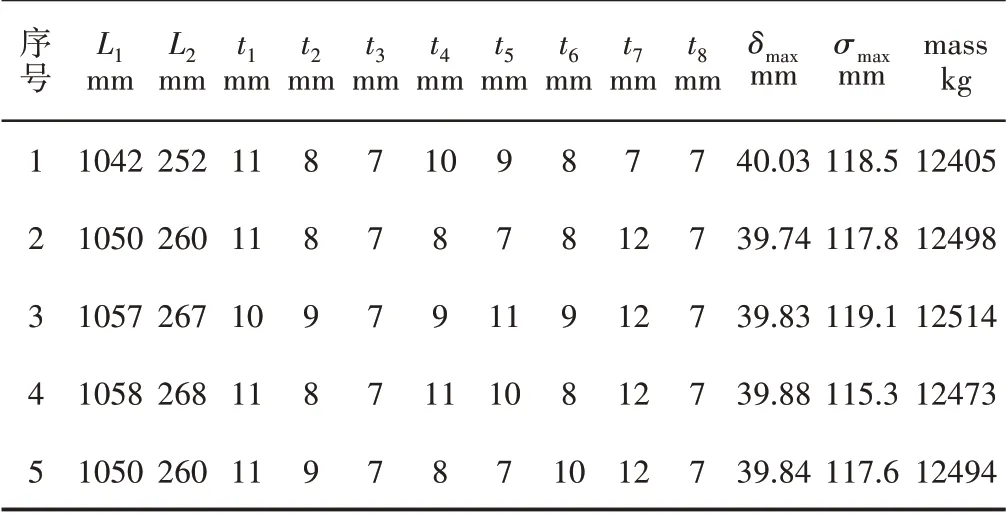
表3 5个最优Pareto解Tab.3 5 Optimal Pareto Solutions

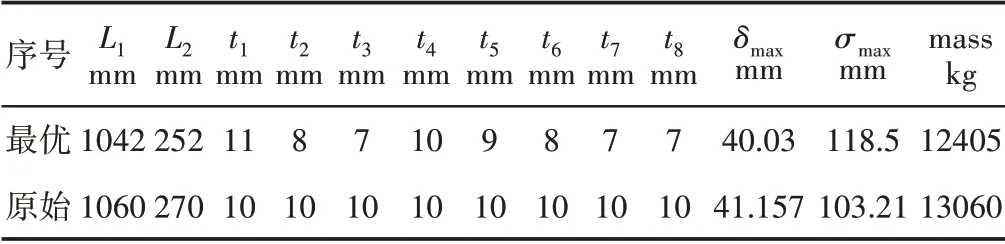
表4 最优方案和原始方案对比Tab.4 Comparison of Optimal and Original Plans

6 结论

这里以双高双立柱堆垛机整体结构为工程实例，提出以三维模型的参数，最佳填充样本空间（OSF）、Kriging模型非支配排序多目标遗传算法（NSGA-II）相结合的多目标静态优化设计方法，其特点为：（1）在双高双立柱堆垛机多目标优化过程中，通过采用最佳样本填充空间（OSF）进行试验设计，在通过Kriging模型构建近似响应面模型代替复杂真实的模型。从而避免优化时调用真实模型的次数，提高优化效率。（2）通过考虑最大应力、最大位移和整机质量等要求，在双高双立柱堆垛机结构多目标优化过程中，通过运用非支配排序多目标遗传算法（NSGA-II）进行寻优获得多个最优的非支配排序Pareto解。（3）通过上述方法能够有效的提高结构设计的效率和质量，对双高双立柱式堆垛机结构设计提供了参考。