Neuberg-Podoe不等式的优美证明与类似
浙江省湖州市双林中学 (邮编:313012)
1891年,J.Neuberg提出了以下著名不等式:设a、b、c与a′、b′、c′分别是两个三角形的三边长、△、△′分别代表它们的面积,猜测成立:
a2(b′2+c′2-a′2)+b2(c′2+a′2-b′2)+c2(a′2+b′2-c′2)≥16△△′
①
1943年,D.Podoe第一个给出了这个猜想的证明,故而称作Neuberg-Podoe不等式.
本文旨在探索Neuberg-Podoe不等式的优美证明,因势利导收获她的两个“类似”. 欣喜之余,与大家分享.
1 Neuberg-Podoe不等式的优美证明
证明记这两个三角形为△ABC与△A′B′C′,其中a、b、c与a′、b′、c′分别为内角A、B、C与A′、B′、C′的对边长,则①式等价于:
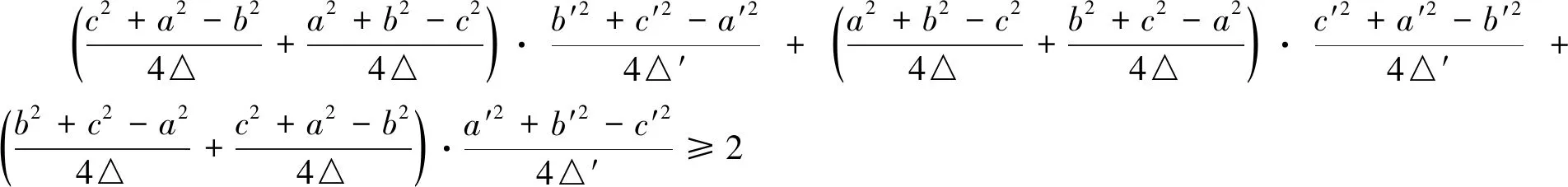
⟺(cotB+cotC)cotA′+(cotC+cotA)cotB′+(cotA+cotB)cotC′≥2
②
⟺(cotA+cotB+cotC)(cotA′+cotB′+cotC′)≥2+cotAcotA′+cotBcotB′+cotCcotC′
③
≥cotAcotA′+cotBcotB′+cotCcotC′+2.
这就证明了③式成立,从而Neuberg-Podoe不等式①获证(当且仅当cotA∶cotA′=cotB∶cotB′=cotC∶cotC′=1∶1,即△ABC与△A′B′C′相似时取“=”号).
基于以上Neuberg-Podoe不等式的优美证明,姑且将等价不等式②与①联袂成:
定理1 设△ABC与△A′B′C′的内角A、B、C与A′、B′、C′的对边长分别是a、b、c与a′、b′、c′,△与△′分别是它们的面积(以下意义相同),则有
(cotB+cotC)cotA′+(cotC+cotA)cotB′+(cotA+cotB)cotC′≥2
②
⟺a2(b′2+c′2-a′2)+b2(c′2+a′2-b′2)+c2(a′2+b′2-c′2)≥16△△′
①
2 Neuberg-Podoe不等式的类似
进而,把三角形恒等式:
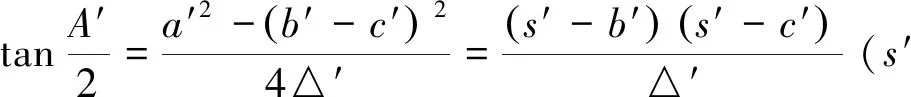
定理2 在△ABC与△A′B′C′中,s′为△A′B′C′的半周长,则有
④
⟺a2(s′-b′)(s′-c′)+b2(s′-c′)(s′-a′)+c2(s′-a′)(s′-b′)≥4△△′
⑤
类似地,还有:
定理3 在△ABC与△A′B′C′中,s与s′为它们的半周长,则有
⟺a(s-a)(s′-b′)(s′-c′)+b(s-b)(s′-c′)(s′-a′)+c(s-c)(s′-a′)(s′-b′)≥2△△′
⑥
定理2与定理3中的⑤式与⑥式就是Neuberg-Podoe不等式的两个类似.

