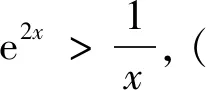微观分析图象 探微寻法悟理
安徽省金寨第一中学 六安市名师工作室 (邮编:237331)
解决函数问题思维切入点从何而来?灵感因何而生?毫无疑问,对图象的分析必不可少,很多时候,灵感来自图象.分析图象有时需要把握全局,分析整体,有时只需微观探究,盯准局部,微观分析,尤其涉及函数零点、极值点问题.笔者在文[1]进行了讨论,近日研究部分高考题,更发现微观分析图象,找到解题灵感之重要性,现举例说明.
1 见微知理
题1(2018年全国高考理科(Ⅲ)卷21题)已知函数f(x)=(2+x+ax2)ln(1+x)-2x.
(1)若a=0,证明:当-1
(2)若x=0是f(x)的极大值点,求a.
分析第二问.函数的定义域是(-1,+∞).由(1)可知a≥0不合题意,只要考虑a<0.现在利用f(x)的微图结合f(x)的导数f′(x)分析.
第一,注意到f(0)=0,f(x)在x=0处连续,若f(x)在x=0处取得极大值,则f(x)在x=0的邻域(-δ,δ)(邻域:本文中指“极小”的区间,下同)内,恒有f(x)≤0,可作出其“微图”,如图1.

图1
第二,f(x)在x=0处取得极大值,则在x=0的邻域(-δ,δ)内f(x)先增后减,f′(x)在x=0处先正后负且f′(0)=0,对应的f′(x)微图应为:在y轴左边图象在x轴上方,y轴右边图象在x轴下方.
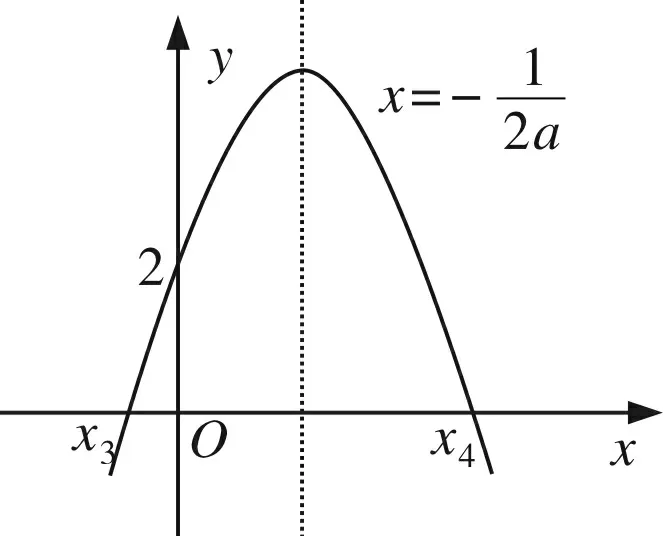
图2
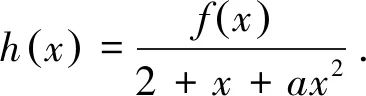
h(x)在x=0的邻域(-δ,δ)内连续,且h(x)=0,在x=0的邻域(-δ,δ)内的微图同图1,这样,问题转化成函数h(x)在x=0处取得极大值(结合微图分析,实现解决极值问题的“函数转化”).下面求出h(x)的导数,再结合“微图”对h(x)的导数h′(x)进行分析.

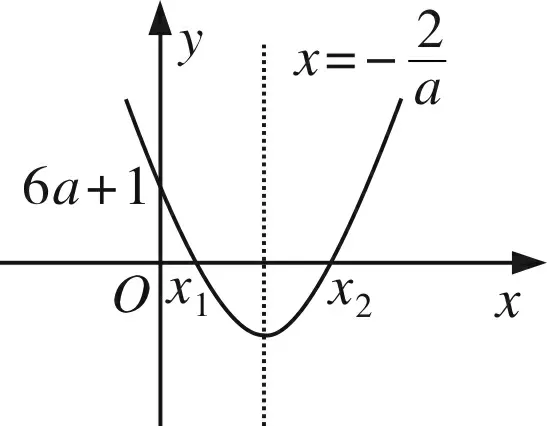
图3
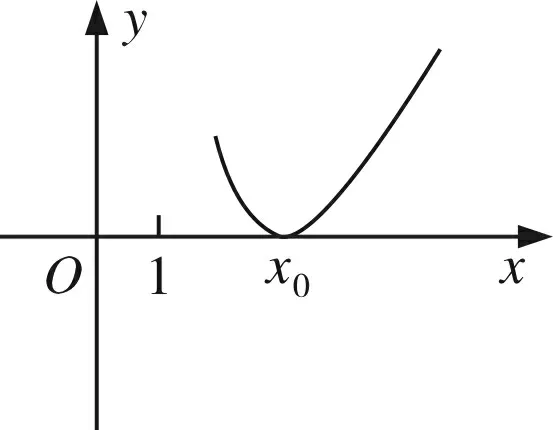
(1)当6a+1>0时,φ(x)如图3(只需关注图象在x=0的邻域(-δ,δ),下同),取δ 图4 (2)当6a+1<0时,φ(x)如图4,取δ 图5 (3)当6a+1=0时,φ(x)如图5,取δ 从上述问题解决过程可以看出,用图象辅助分析函数极值不一定要分析函数或导函数的整体状况,只要探究极值点附近如何变化(这一点很重要,它可以避免了暂时对参数的讨论),瞄准极值点附近函数局部图象,局部放大,微观分析.因此,凡涉及极值问题,在分析图象时均要想到“微图分析”,既要分析函数在极值点附近的微图,看“单调变化”;又要分析导函数在其零点附近的微图,看“正负变化”,观察导函数正负“走向”,如:是正负不变,还是由正变负或由负变正?从而知道函数能否取到极值,是极大值还是极小值. 微观分析,也是极限思想的应用,如构造函数h(x)时,在x=0的邻域(-δ,δ)内,2+x+ax2>0,h(x)与f(x)同号;分析导数h′(x)时,在x=0的邻域(-δ,δ)内,(1+x)>0,2+x+ax2>0,使问题简化. 题2(山东省2015年高考理科21)设函数f(x)=ln(x+1)+a(x2-x),其中a∈R. (1)讨论函数f(x)极值点的个数,并说明理由; (2)若∀x>0,f(x)≥0成立,求a的取值范围. 分析第二问.显然a<0不合题意,a=0,合题意.现在分析a>0时的情形. 虽然不知道f(x)在(0,+∞)整体单调性,但由于f(0)=0,所以微区间(0,δ)内,f(x)必然单增,亦即通过“微区间”分析,使隐含的信息凸显(如本例中在(0,δ)内函数必须单增),使问题解决的思维暴露.同样的方法可以解决以下问题. 题3 (2017年全国高考理科(Ⅲ)卷21题)已知函数f(x)=x-1-alnx. (1)若f(x)≥0,求a的值; (2)略. 图6 分析(1)函数定义域为(0,+∞),注意到f(1)=0,f(x)连续,因此,若f(x)≥0,则在x=1的邻域内函数微图如图6,即x=1是函数极小值点,所以f′(1)=0,a=1(f(x)≥0的必要条件),现在只要证明a=1时,f(x)≥0即可(易证,过程略). 题4(四川省2015年高考理科21题)已知函数f(x)=-2(x+a)lnx+x2-2ax-2a2+a,其中a>0. (1)设g(x)是f(x)的导函数,讨论g(x)的单调性; (2)证明:存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解. 简析第二问难度很大,用微图辅助分析. 图7 微图分析使我们发现了隐含较深的“关系”,找到了问题解决的切入点.本例中,x0既是零点又是极小值点,满足f′(x0)=0和f(x0)=0,并利用f′(x0)=0实现变量之间转化. 函数零点问题中,我们经常要求零点所在区间或证明某一单调区间上存在零点,用零点附近的微图能够确定解决问题的努力方向,再结合不等式放缩分析求解. 题5 (2017年全国高考理科I卷21题)已知函数f(x)=ae2x+(a-2)ex-x. (1)讨论f(x)的单调性; (2)若f(x)有两个零点,求a的取值范围. 图8 而当0 由于求f(x)的零点或得出f(ξ)>0的点ξ比较困难,考虑放缩成比原函数小且能够求出零点的函数(图中的虚线部分,一般与原函数在放缩的区间上单调性一致). ①先考虑区间(-lna,+∞),怎样找到使f(ξ)>0的ξ值呢?关键是在区间(-lna,+∞)上找到比f(x)小的函数φ(x)(这是微图分析的结果). 由于x>0时,ex>x,当aex+(a-2)>0时(注:只要x>ln(2-a),就有aex+(a-2)>0成立,我们就在x>ln(2-a)时进行放缩), f(x)=ae2x+(a-2)ex-x=ex[aex+(a-2)]-x>x[aex+(a-2)]-x. ②再分析在区间(-∞,-lna)上能否寻找到使f(ξ)>0的ξ值.事实上,可以通过“试取”的方法得到ξ,但为了说明微图的作用,并利用放缩法求解,同样用上述方法分析. 图9 当然,放缩的方式有无数种,但无论如何变式,都是基于对零点附近图象探究而得到的启发.如果零点附近图象如图9(实线代表原函数,虚线代表放缩后的函数),则放缩应朝着大于原函数的方向进行. 用图微观分析的作用是:怎样通过放缩找到并证明包含函数零点的区间端点.图象是不等式放缩的直观显现和几何解释,学生理解更易.如果不用微图分析,学生有时很难理解为什么要用不等式放缩,为什么朝着比原函数小(或者大)的函数方向放缩. 准确作图,以微图分析,是基本的数学能力,养成用图分析的习惯,是基本数学素养的体现,微图使思维“可视”,微图使思维插上翅膀.函数教学时,要培养学生作图用图的意识,以图助思维,以图寻思路.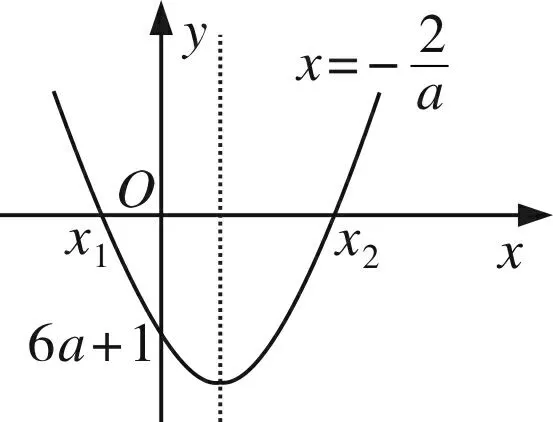


2 探微索果
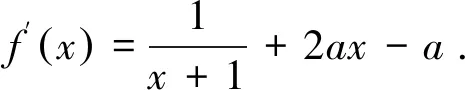


3 以微定向