数学质疑式阅读能力刍议

山东师范大学数学与统计学院 (邮编：250014)

山东省烟台第二中学 权 奎 (邮编：264000)

1 数学质疑式阅读能力的内涵

数学阅读是数学学习的重要方式之一.社会的信息化发展使得人类的阅读活动日趋复杂，阅读内容的呈现方式多样化.其中，数学相关材料的阅读成为现代信息社会对人的信息素养的要求之一.

数学质疑式阅读能力是在数学质疑式阅读活动中需要培养的能力，是数学教师在引导学生进行自主课前预习、阅读课本和数学探究活动中，由学生产生困惑或提出有价值的问题，通过师生互动交流合作、质疑提升，共同解决疑惑，最终使学生理解和体会数学内容和方法的本质，并能消化吸收加以应用的一种阅读能力.

培养学生的质疑能力和创新精神是在数学学科中实施素质教育的重要内容之一.数学质疑式阅读能力是学生的质疑能力和创新精神的重要体现，在数学教学过程中，只有熟练运用这种能力才能更好地进行数学质疑式阅读活动，从而完成质疑式数学教学过程.

数学质疑式阅读能力是在数学质疑式阅读活动过程中培养发展起来的.对此，目前有不少研究.例如，李兴贵[1]提出，数学阅读过程同一般阅读过程一样，是一个完整的心理活动过程，包括对语言符号(文字、数学符号、术语、公式、图表等)的感知和认读、新概念的同化或顺应、阅读材料的理解和记忆等各种心理活动因素.同样地，数学质疑式阅读首先与一般性的数学阅读过程一样，是一个需要不断假设、想象、推理、验证的积极能动的认知过程，同时也是对数学概念、定理、公式、法则等不断激起学生认知内部的矛盾冲突，并通过师生间的质疑、释疑、解疑等完整的心理活动过程.数学质疑式阅读过程的认知对象是数学材料，包括各类概念、命题、例题、习题，和以数学语言为载体的数学系统知识的逻辑表述.傅海伦[2]提出，数学除了抽象性、严谨性和应用的广泛性外，还有十分丰富的思维方法和简约、通用的语言系统、符号体系，这些特点使得数学质疑式阅读有与传统阅读不同的要求，体现在具体方面则是语言转化方面、问题解决方面和信息获取方面等方面的各种能力.

2 数学质疑式阅读能力的分类

数学质疑式阅读究竟应该包括哪些方面的能力？如何对数学质疑式阅读能力进行分类？目前并没有一致的说法，也没有统一的分类标准.李兴贵[3]将数学阅读能力分为语言转化能力、逻辑思维能力和元阅读能力.也有研究者[4]将数学阅读能力分为数学材料形式化能力、概括数学材料能力、联想能力、辨别数学材料的能力、对所读数学材料的应用能力等.笔者尝试通过数学质疑式阅读活动的语言转化、问题解决和信息获取这三个具体的方面，对数学质疑式阅读能力进行分类研究.

2.1 语言转化方面的数学质疑式阅读能力

数学的简约、通用的语言系统与文字语言相结合，方便传达各种数学知识与数学信息，这就要求学习者在数学质疑式阅读活动过程中有将各种文字语言、符号语言、图形语言等进行相互转化的能力.

(1)文字语言符号化能力

通过数学质疑式阅读将文字语言进行符号化的能力，是语言转化方面最基本的数学质疑式阅读能力.在指导学生进行数学史和数学文化材料的阅读中，尤其需要培养学生的这种能力.傅海伦[5]在对各类中国传统数学思想方法进行分析时，特别强调中国古代的数学经典名著《九章算术》等就十分重视这种基本能力.古代数学内容以文字形式呈现，通过对文字语言进行符号转化，只有具备了这种文字语言符号化能力才能为后人阅读文献、准确进行解读与分析奠定必要的基础.例如，《九章算术》勾股章一开始讲了勾股定理及其变形，前三个题的“勾股术曰：勾股各自乘，并而开方除之，即弦.又股自乘，以减弦自乘，其余开方除之，即勾.又勾自乘，以减弦自乘，其余开方除之，即股”.

如果以a、b、c各表示直角三角形的勾、股、弦.则上述三句话可表示为

这种符号转化，既可以方便理解与记忆，又可以更简洁地交流和应用，这给我们现代人以重要启示：文字语言的各种词语界定了具体的运算，进行数学质疑式阅读活动时必须具备文字语言符号化的能力，不能漏字和颠倒次序.

(2)符号语言文字化能力

数学常用符号进行记录与分析，这种符号方便已了解符号意义的学习者理解与记忆具体数学知识与数学信息.在对学生的数理逻辑教学中，可以渗透使用多种符号语言进行逻辑推理与相关分析，例如著名的苏格拉底论证可以写成符号语言：

(∀x)(H(x)→M(x))∧H(s)⟹M(s)

其中，H(x):x是一个人，M(x):x是要死的，s:苏格拉底.

转化成文字语言其实就是苏格拉底论证：人都是要死的，苏格拉底是人，所以苏格拉底是要死的.

将符号语言转化成文字的能力不仅仅是高等数学研究常用到的能力，在小学数学与中学数学的学习过程中也常常需要应用这种能力.

(3)图形语言转化能力

数学中有各种各样的图形与表格，例如函数图象、几何图形、程序框图、数值表、统计表等.将这些图形与表格中包含的各种信息转化为文字语言或者符号语言的能力，就是图形语言转化能力.

在高中学习三角函数的时候，需要从三角函数图象中获得相关信息，如下图：

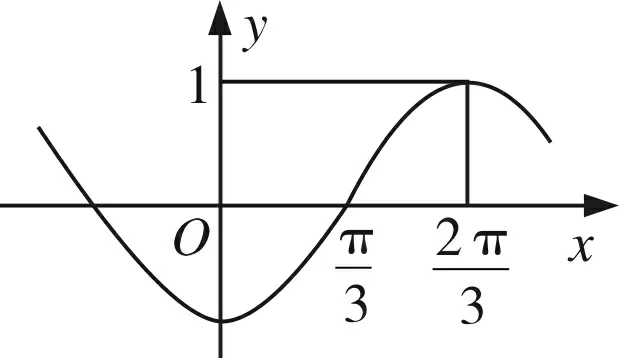
2.2 问题解决方面的数学质疑式阅读能力

喻平[6]认为，问题解决是在概念、命题学习的基础上，应用知识去解决问题的学习形式.在解决一个问题的过程中，学习者也会学到某些新知识.问题解决从宏观角度看，是让学习者运用数学知识解决现实问题或将现实问题进行数学建模的形式，从微观角度看，是让学习者解决某一知识点或某一学段的数学习题的形式.问题解决能够培养学习者应用数学的意识和能力，从而体会到数学的应用意义.

数学质疑式阅读能力在问题解决方面，主要作用于对已知条件的解读能力和对问题解决思路的分析能力.

(1)对已知条件的解读能力

在质疑式数学阅读过程中，对题目已知条件的认真解读与否决定了解决问题的对错，例如有这样的一个已知条件：

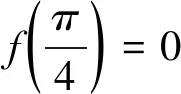
(2)对问题解决思路分析能力

对于质疑过程中提出的问题，通过质疑式阅读，先将题目的已知条件分析透彻，之后要考虑怎样解决题目要求解的问题，即问题解决的思路是什么.

例如，已经将已知条件整理成了最简单的形式tanα=-3，待求解问题是

由于分子的式子与倍角公式很相似，部分学生马上套用倍角公式进行转化，但是在转化后却不知如何进行，因为已知条件与倍角没有明显关系.

其次，对于有待解决的质疑问题，通过质疑式阅读，还可以考虑在只知道一个值的情况下求式子的解，最理想的情况莫过于将式子转化成只有已知值的形式.分子的两项又都是两个三角函数相乘，可以尝试在分子上加分母1，从而

由于sin2α+cos2α=1，可以带入进行约分，转化成只含tanα的形式，赋值即可解决，这样能收到好的效果.

2.3 信息获取方面的数学质疑式阅读能力

数学包括数学思维与数学知识，随着社会的信息化发展，信息的获取越来越重要，能不能从各种各类信息中获得需要的信息是一个人信息获取能力的重要体现.结合数学学科，数学质疑式阅读在信息获取方面需要学习者在各种形式各种载体的信息中获得与数学知识和问题解决方法有关的信息.具体来说，这种能力既包括对关键信息的提取能力，又包括对信息中蕴含的数学知识进行有效检索和应用能力，不仅可以提高学生的思维品质，还有利于培养学生的质疑能力和创新精神.

(1)关键信息的提取能力

数学思维能力主要考虑从相关信息中获取数学思维的能力.即通过阅读相关信息，是否能获取某些数学思维并运用于之后的问题解决中.

例如，《孙子算经》中记载了这样的一道题：“今有雏兔同笼，上有三十五头，下有九十四足，问雏兔各几何？”现行的解题思路一般是列方程求解，但古时提出了“半其足”的巧妙算法.这里的“半其足”就是最为关键的信息.翻译成现代的解释是：数一数所有鸡和兔一半的脚，则每只鸡就变成了“独脚鸡”，而每只兔就变成了“双脚兔”.这样，“独脚鸡”和“双脚兔”的脚就由94只变成了47只；而每只“鸡”的头数与脚数之比变为1:1，每只“兔”的头数与脚数之比变为1∶2.由此可知，有一只“双脚兔”，脚的数量就会比头的数量多1.所以，“独脚鸡”和“双脚兔”的脚的数量与他们的头的数量之差，就是兔子的只数，即：47-35=12(只)；鸡的数量就是：35-12=23(只).

通过对上述数学质疑式阅读材料的分析，关键信息的提取能力十分重要，这种阅读能力不仅可以帮助学习者准确理解问题的实质，把握解题规律，而且可以获取一题多解、假设求解、比列求解等多种解题思路，从而拓展学习者的思维.

(2)数学知识信息的检索能力

数学知识信息的检索能力主要考虑从相关信息中及时检索到已有数学知识的能力.例如，在向学习者介绍黄金分割之后，学习者能否应用这一数学知识解决实际问题，以检验学习者是否真正获取了数学知识.

黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值约为0.618.这个比例被公认为是最能引起美感的比例，因此被称为黄金分割.

对于问题[7]：女士应该穿多高的高跟鞋看起来最美？

学生在遇到这个问题时，立马能检索到黄金分割的知识信息：人下肢与身高比为黄金分割时看起来最美.设女士身高为lcm，下肢躯干部分为xcm，鞋跟高为dcm.可列式：

从而迅速巧妙地解决问题.

3 总结

数学质疑式阅读能力有不同方面的具体体现.这种不同并不冲突，不同方面的数学质疑式阅读能力往往需要共同发挥作用以实现真正高效的数学质疑式阅读活动.例如信息获取方面的数学质疑式阅读能力，往往需要语言转化方面的文字语言符号化能力，同时还可能作用于问题解决方面的解决思路分析能力，等等.因此，培养学习者的数学质疑式阅读能力，要结合学习者的特点，依据阅读目的和学习要求，从不同方面综合分析后进行针对性的培养.