错在哪里
2019-04-18 03:41邮编473061
中学数学教学 2019年2期
(邮编:473061)
1 河南省南阳师范学院软件学院
题目已知函数f(x)=3x-b(2≤x≤4)的图象过点(2,1),则F(x)=[f-1(x)]2-f-1(x2)的值域为______.
错解由题意得f(2)=32-b=1,
所以b=2,f(x)=3x-2.
因为函数f(x)的定义域为[2,4],所以
2≤f-1(x)≤4,0≤log3x≤2,
又F(x)=[f-1(x)]2-f-1(x2)
=(2+log3x)2-(2+log3x2)
=(1+log3x)2+1,
所以2≤F(x)≤10,
故函数F(x)的值域为[2,10].
解答错了!错在哪里?
上述解答过程中,没有注意到函数f-1(x)的定义域为[1,9],忽视了f-1(x2)的定义域并非为[1,9],从而将函数F(x)的定义域也视为[1,9],没有理清函数的基本概念.
正解由上述解答可得,
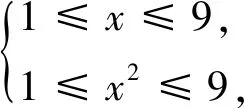
所以F(x)的定义域为[1,3],所以2≤F(x)≤5,故函数F(x)的值域为[2,5].
2 新疆乌鲁木齐市第八中学
李昌成(邮编:830002)
题目(《小题大做》2019版,教师用书第131页)已知函数
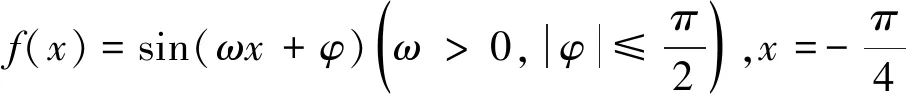
A.11 B.9 C.7 D.5
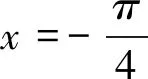
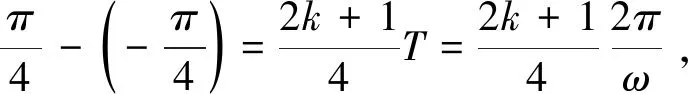
ω=2k+1(k∈N).
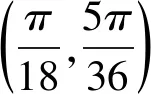
所以ω≤12,由此得ω的最大值为11,故选A.
解答错了!错在哪里?
由于ω是奇数,且ω≤12,因此我们从满足这两个条件的最大值开始验证.
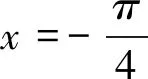
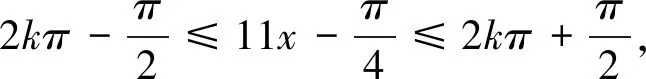
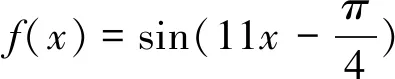
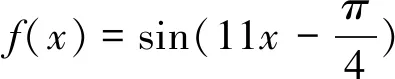
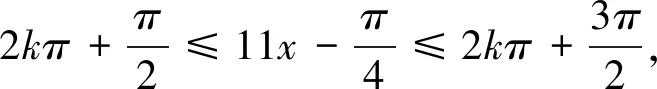
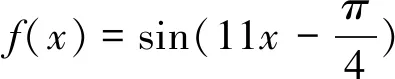
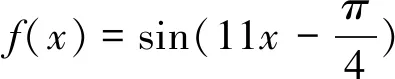
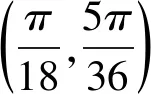
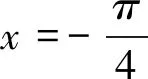
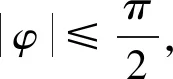
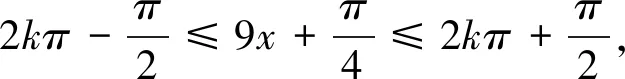
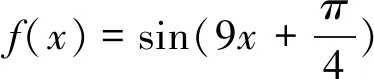
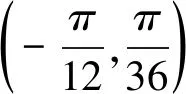
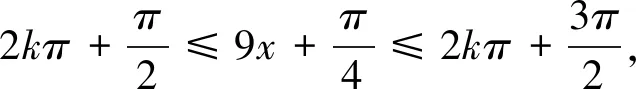
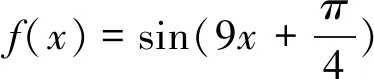
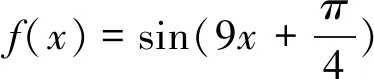
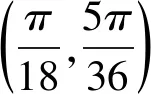
所以ω的最大值为9.故选B.
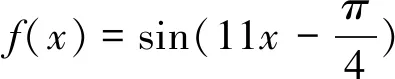
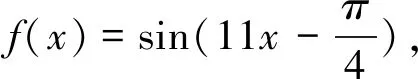
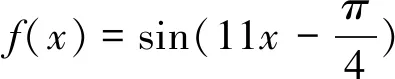
对于ω的奇偶性还可以如下论证.
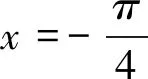
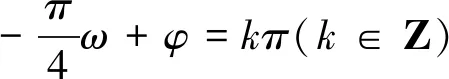
①
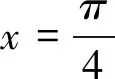
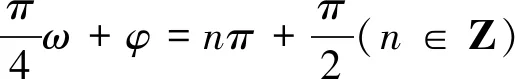
②
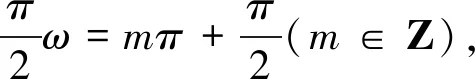
通过以上研究,我们既发现了问题,也解决了问题,对于巩固学生的基础知识,培养严谨的逻辑思维,提高学生数学核心素养是大有裨益的.
猜你喜欢
语数外学习·高中版上旬(2022年2期)2022-04-09
新世纪智能(数学备考)(2021年9期)2021-11-24
新世纪智能(数学备考)(2021年9期)2021-11-24
新世纪智能(数学备考)(2020年9期)2021-01-04
新世纪智能(数学备考)(2020年9期)2021-01-04
读写算(2019年5期)2019-09-01
中学生数理化·高一版(2018年10期)2018-11-08
中学生数理化·高一版(2018年9期)2018-10-09
上海师范大学学报·自然科学版(2018年3期)2018-05-14
理科考试研究·高中(2017年10期)2018-03-07

