对一道高考压轴题的深度探究
湖南省长沙市明德中学 (邮编:410009)
近日笔者在上一堂高三习题课时,讲到一道2016年高考浙江卷的压轴题,不料一波三折,“被迫”与学生一道对该题进行了深度探究.

图1
1 试题再现
(1)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(2)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
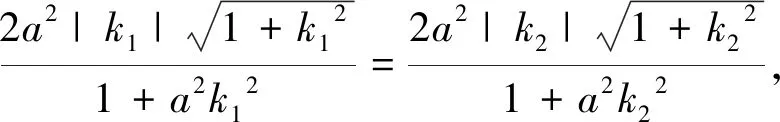

笔者按照上述标准答案的解法讲解了该题,指出关键是求出a2的取值范围,并着重点评了“正难则反”的思维,本以为这样就可以完美收官了,但学生们普遍表现出一种欲言又止,心有不甘的表情,一方面对“正难则反”的方法啧啧称叹,一方面对自己从正面解题的方法也觉得不无道理,一时间大家各抒己见,争论不休.
2 华山论剑

图2

该生是凭借几何直观构造图形,但立刻遭到其他同学反驳.
生2:我认为在圆A变大时虽然点B不再是公共点,但可能在两侧产生新的公共点,所以这个椭圆并不满足与圆至多3个公共点的要求.
师:生2的怀疑确实不无道理,毕竟感性认识不具备理性的说服力,可否从理性的角度来解析呢?

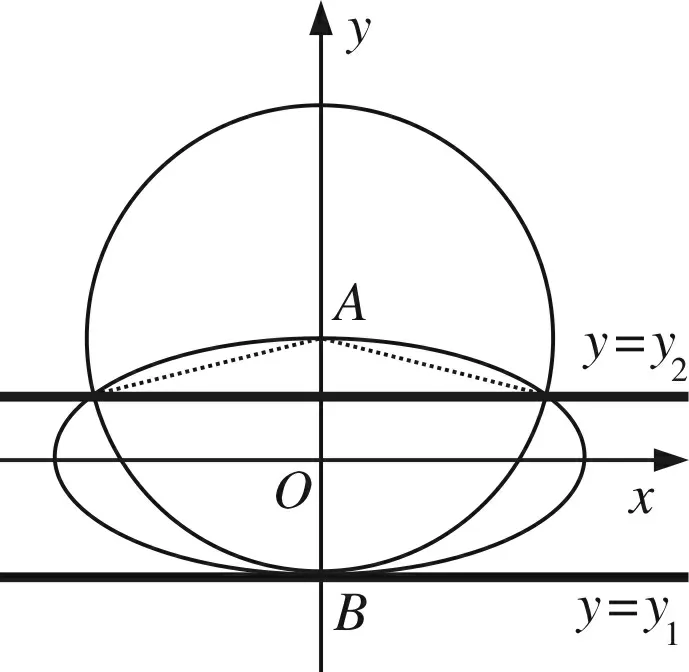
图3

很明显此刻同学们的兴趣和疑惑更大了,一方面联立方程利用数形结合解题是大家常用的方法,另一方面两种结果竟然恰好相反,大家都把目光投向了教师,看来不搞个水落石出决不罢休了,于是笔者和同学们共同展开了对本题的深度探究.
3 深度探究
师:同学们专注于计算恰好3个公共点的情况,然而本题是要寻找这样一类椭圆,即无论圆A大小怎样变化,都至多3个公共点,因此不应局限在恰好3个公共点而止步不前,还要看在变化过程中是否出现4个公共点.

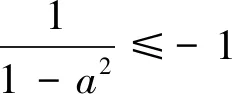
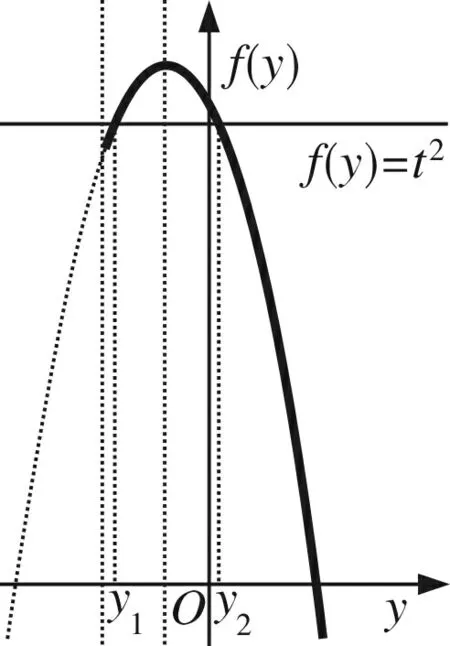
(1)当r2>f(-1)=4,即r>|AB|时,方程f(y)=r2无解,此时0个公共点;
(2)当r2=f(-1)=4,即r=|AB|时,方程f(y)=r2有唯一解y1=-1,此时对应1个
公共点(如图4、5) .

图4
(3)当0=f(1) 图6 图8 此时对应有4个公共点(如图10、11); 图10 (4)当r2=f(-1)=4,即r=|AB|时,方程f(y)=r2有两个不同的解y1=-1,y2∈(-1,1),此时对应有3个公共点(如图12、13); 图12 (5)当0 图14 综上所述,当1 揭开庐山真面目,学生的满腹疑惑终于烟消云散,通过深度探究,训练了对函数的综合运用能力,强化了数形结合的思维,相信对提升学生包括逻辑推理等在内的核心素养大有裨益.


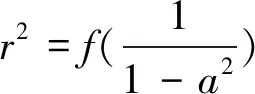




4 尘埃落定

