一次现场命题比赛的全记录

浙江省金华市第六中学 (邮编：321000)

为了加强新高考背景下数学复习的信息交流，增进数学复习的经验共享，增强复习的针对性和实效性，提升教师的命题能力，浙江省金华市教研室决定于11月27日13:30-16:30在浙师大附中举办金华市首届高中数学现场命题比赛.由举办方提供命题背景和命题方向，以校为单位(每单位三名高三教师)组队报名参加，比赛自带电脑，可带资料，但比赛时不允许上网.笔者有幸参加了此次现场命题比赛，并荣获金华市一等奖．经过抽签，得到如下命题材料.

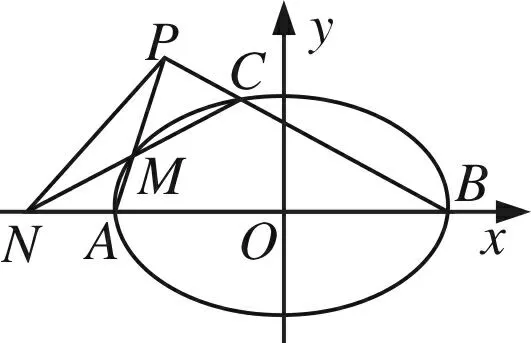
解析几何现场命题试题

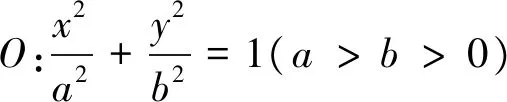
要求请你改变“A、B是椭圆长轴上的两个顶点”状态为“某种符合条件的两点”，命制一道具有浙江特色的高考题，并做简要解答. 现将本次现场命题比赛活动记录如下，供同行批评指正．

1 背景解读

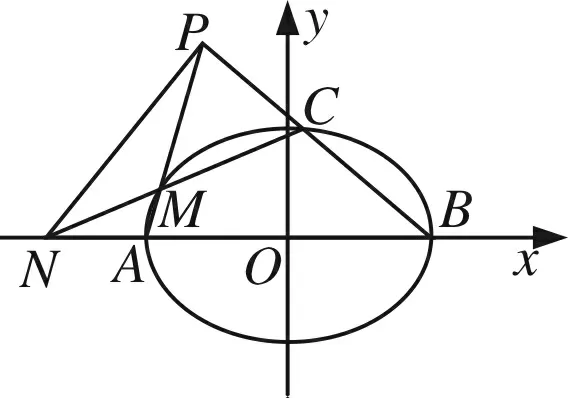
图1

借助几何画板对满足上述条件的问题进行了演示，立马就可以测算出数值，如图1所示，图形变化过程中数量关系的变化(哪怕是微小的变化)也可以直观地显示出来. 笔者欣喜地发现，在连续改变交点P坐标数值时，不影响结论成立. 其实这是一个与圆锥曲线极点和极线有关的一个统一等差定理[1].

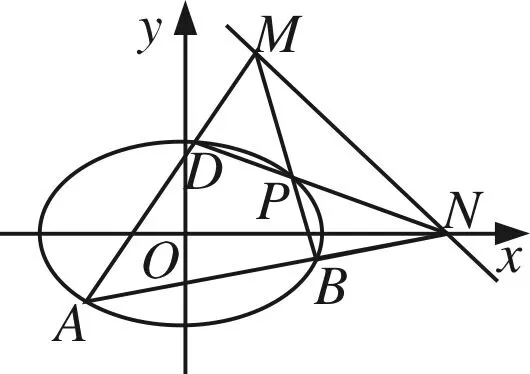
图2

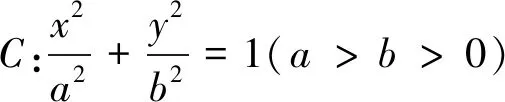
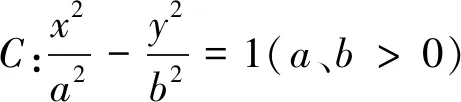
定理3 点A、B、D、P是抛物线C:y2=2px(p>0)上四点，直线AB、DP交x轴于点N，直线AD交BP于点M，设AD、BP、MN的斜率为k1、k2、k3，则k1+k2=2k3．

2 题源追溯

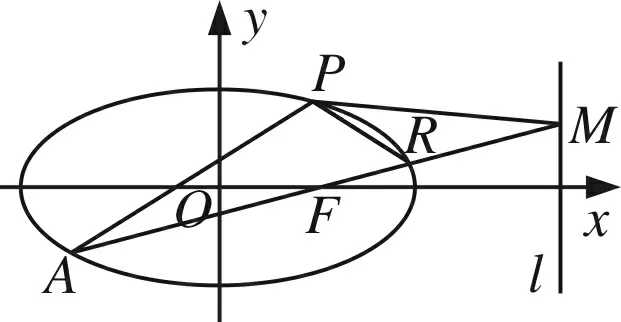
图3

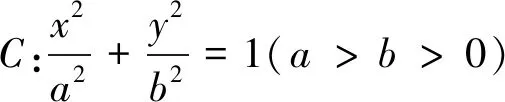
(1)求椭圆C的方程；

(2)AB是经过右焦点F的任一弦(不经过点P)，设直线AB与直线l相交于点M，记PA、PB、PM的斜率分别为k1、k2、k3.问：是否存在常数λ，使得k1+k2=λk3？若存在，求λ的值；若不存在，说明理由．

题源2 (2013年高考江西卷文科20题)

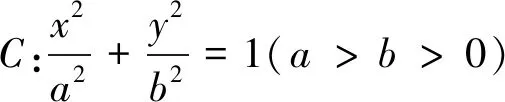
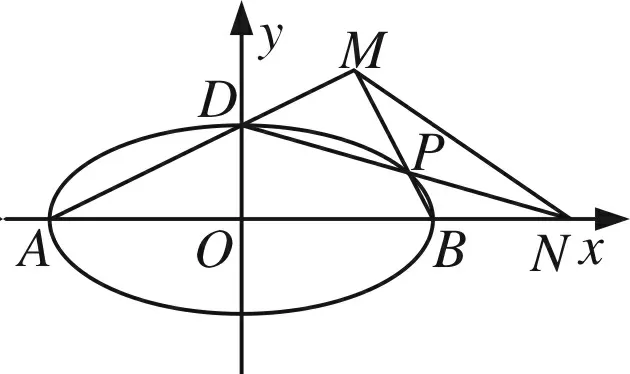
图4

(1)求椭圆C的方程；

(2)如图4所示，A、B、D是椭圆C的顶点，P是椭圆C上除顶点外的任意点，直线DP交x轴于点N，直线AD交BP于点M，设BP的斜率为k，MN的斜率为m，证明：2m-k为定值．

每年的高考试题似乎都出乎意料，却又在情理之中．2013年高考江西文理卷中的解析几何解答题更是堪称经典，赏析之余，无不佩服命题者的深厚功底和良苦用心．对这些题进行深入研究，并对其进行改编是命制高考模拟试题的常用着力点．

3 命题历程

3.1 立意与选材

立意是确定试题的编写意图，明确考查目的(考查哪几种能力？哪种能力为主？哪种能力为兼顾？考查哪个学科分支？考查哪部分内容？等等)，立意是核心，选材应服务于立意．根据抽签材料上的要求，笔者拟命制一道圆锥曲线的综合试题，着重考查直线方程、直线斜率及直线与圆锥曲线相交等知识，旨在考查学生的逻辑推理、直观想象、数学运算等核心素养．

3.2 联系与搭架

波利亚说：“类比是伟大的引路人．” 圆与椭圆、双曲线、抛物线 “同宗同源”，那么圆是否具有上述类似结论成立？同时受到题源2定值问题的启示，特初拟了如下试题．

命题1 已知圆O:x2+y2=1与x轴交于A、B两点，与y轴交于点C,M是圆O上任意一点(除去圆O与两坐标轴的交点)．直线AM与BC交于点P,直线CM与x轴交于点N,设直线PM、PN的斜率分别为m、n，求证：m-2n为定值．

为了减少运算的盲目性，借助几何画板对满足上述信息的问题进行了演示，发现m-2n始终为定值1，从而确保了命题的正确性．定值问题求解方法通常有两种：一是特殊值求法，即将问题条件特殊化，再证明所特殊化后的定值与变量无关；二是直接推理、计算，将要求的定值表示为某个变量的函数关系，再化简这个关系消去变量，从而得到定值．本题设点为参数或设斜率为参数均可顺利求解，有兴趣的读者可试一试．同时，设计试题框架时应注意主干硬朗，层次分明，从而形成坯胎．试题坯胎要具有一定的弹性和伸缩性，即题设条件便于增加或减少，提问角度可提供调换，试题难度容易调节，方便加工与调整．

3.3 加工与调整

2017年浙江高考数学试卷，打破了高考中文科生和理科生的固定思维模式，开启了文理合卷的新篇章．解析几何解答题作为浙江新高考次压轴题，应充分考查学生的思维品质与学习潜能，彰显对数学核心素养的考查要求．由命题1的解答过程来看，此题中的圆锥曲线以圆为载体，则略显平和，缺乏必要梯度．同时受题源1、2定值问题的启发，在随后的多地高考模拟卷中出现了类似问题，新颖性不够．而一道优质的试题往往是命题者研究成果的结晶，在同一个背景下，交换部分条件和结论，便可生成一道新题．笔者结合对相关题目的研究[2]，可得到以下试题．

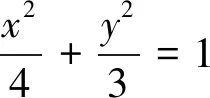
试题的加工和调整，首先确保试题的科学性和适纲性，其次是精心调节难度．难度调节必须以整卷的难度分布为依据，常用的调节方法有：改变提问方式，将结论隐藏变为探索式可以提高难度，增设中间问可降低难度；改变题设条件，条件隐蔽化或明朗化，直接化或间接化、具体化或抽象化均可调节难度；改变综合程度，增减知识点的组合，调整解题方法的结构，变换知识和方法的综合广度与深度．

3.4 复核与定稿

随着新课改的深入进行，探究存在性问题越来越受到命题者的青睐，更是高考试卷中的常客．而解析几何中的探究存在性问题主要考查学生探索解题途径，解决非传统完备问题的能力，将数学知识有机结合并赋予新的情境创设而成的，要求考生自己观察、分析、创造性地运用所学知识和方法解决问题．凸显这一特性，命题2略显不足，基于此，笔者作了微调，获得了下述试题．

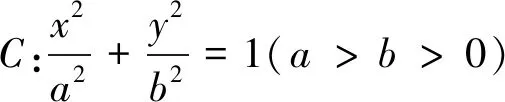
(1)求椭圆C的标准方程；

(2)若直线PA、PM、PB的斜率存在且成等差数列，试问直线AB是否过定点？若过定点，请求出定点坐标；若不过定点，请说明理由．

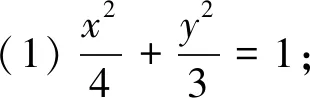
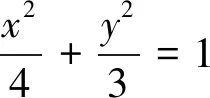
由韦达定理得

当x=4时，则y=4k+m,所以点M的坐标为(4,4k+m).

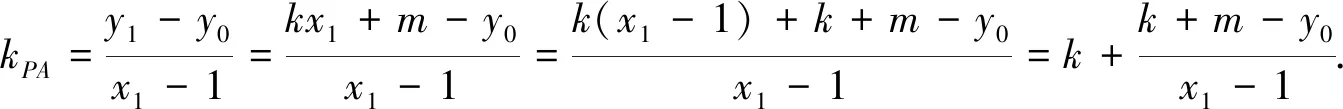
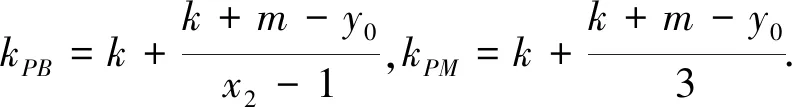
于是kPA+kPB

由直线PA、PM、PB的斜率成等差数列，得

由于l不经过点P,则k+m-y0≠0,故

化简得(m+k)(m+4k)=0.

当m=-k时，则直线AB的方程为y=kx-k,必过定点(1,0)；

当m=-4k时，则直线AB的方程为y=kx-4k,必过定点(4,0)．

综上，直线AB必过定点(1,0)或(4,0)．

复核工作通常需要两人以上进行，才能防止先入为主，重新细写答案，尽可能把各种可能的解答都写出来进行比较，以保证达到考查目的．往往有可能发现更简洁的解法，可能出现其考查的有效性与预先的设计意图大相径庭，如出现这种情况有时会前功尽弃，推倒重来．复核的另一项工作就是文字功夫，对试题的字词句及数学符号都要一一推敲，连标点符号也不能放过．对每一个细节都得顾及，包括试题的陈述和答案的编写，都在这一步完成．

4 点滴感悟

命题很难无中生有，教师需要解题经验的积累，需要命题素材的挖掘，需要理念素养的熏陶，需要命题技术的提升．一道试题的成型往往意味着时间的投入和精力的付出，同时得到经验的积累和能力的提升．只要我们能做一个有心人，勤奋钻研，点滴积累，就会在专业上得到很大提高．