瞄准通法 凸显过程
——记一节高三一轮后的复习课
安徽省淮南市教育局中小学教研室 (邮编:232001)
1 问题提出
《普通高中数学课程标准(2017年)》明确指出“高中数学学习活动不应只限于接受、记忆、模仿和练习,还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.”教学目标的实现要靠学生在学习过程中不断积累基本的活动经验,并运用已有数学知识及其所蕴含的数学思想方法去解决问题,由此在此过程中感悟数学学习的价值和作用,提高学生的数学素养.
历年高考数学考试大纲均明确将“注重通性通法,强化特殊技巧”作为一条重要命题原则.这就是要求教师提高对所教内容的理解水平,增强辨别和判断能力,并在数学中引导学生去分析、总结、体会哪些是“雕虫小技”,哪些是“通性通法”,逐步提高学生的解题能力和数学素养,最终落实数学学科的育人功能.
高三教学后期(一轮已结束)尽管复习已到位,但需要对一系列相对零散知识与方法进行重组,构纬联经,形成网络.但正是因为如此,教师的教学组织更要彰显“过程”与“通法”,充分调动学生的主动性.以下结合笔者听评的一节高三复习课,以求“管中窥豹”,并向各位求教与汇报.
2 课堂实录
出示一道经典例题:
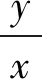
师:请问这道如何求解,请大家发表看法.
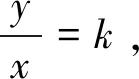
师:这个方法不错,不妨称之为判别式法(投影生1解题过程).
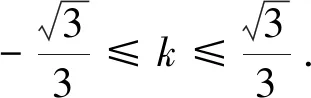
师:本题还有其它解法吗?
生2:由生1的设法y=kx表示直线,(x-2)2+y2=1表示圆,故还可以利用直线与圆的位置关系来求解.
师:这个想法很自然,我们称之为几何法(投影生2的解题过程).
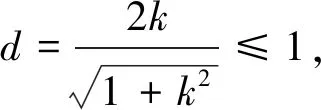

师:本题是否仅有此两种解法呢?

生3:还有更简洁解法,几乎可以“秒杀”!
师:还有如此玄妙的解法?赶快贡献出来与我们一同分享吧!


注意|OC|=2,|AC|=1,则∠AOC=∠BOC=30°,故
师:这个方法以形助数,借形解数,妙不可言,称之为数形结合法.本题已有三种解法,估计差不多了吧?
生4:还有一种解法.
师:请你说说看.
生4:可利用圆的参数方程进行三角换元解决(投影生4的解法).
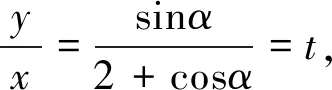
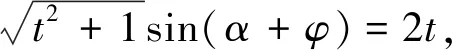
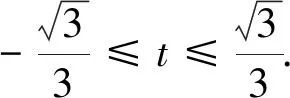
师:刚才大家一共找到四个办法共同解决了一个问题,可谓“异曲同工”.那么在以后解题应该如何选取最有效的方法呢?接下来再看几个题目,请大家思考,讨论下列各题可采用什么方法?(引导学生先讨论再回答)
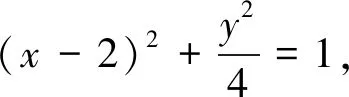
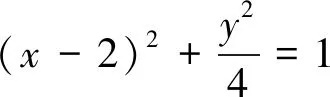
师:为何不用几何法?
生5:因为目前我们还不能从几何直观上判定直线与椭圆位置关系.
师:很好!那么“数形结合”你是如何求解呢?
生5:过原点向椭圆引切线,求出切线斜率.
师:如何求切线斜率?
生5:利用判别式.
师:那么该“数形结合法”本质上说仍是判别式法.故本题通法为“判别式法”与“三角换元法”.(解题过程略)
变式2 若实数x、y满足x2+xy+y-3=0,试求2x+3y的最值.
生6:本题只能用判别式法.
师:请说一说你的理由.
生6:因为x2+xy+y-3=0只是一个二元二次方程,其几何意义并不清楚.
师:很好!看来“判别式法”是一个无所不能的好办法,应该算是我们常谈的“通性通法”,那么它会不会也有“失败”的时候呢?
变式3 若实数x、y满足(x-2)2+y2=1,试求x2+y2+2x-4y的最值.
师:这道题可用判别式吗?为什么?
生7:不可以,因为所求结果不是一次式,不能进行消元.
师:那么它该如何求解呢?
生7:可用三角换元(投影生7的解法)
令x=cosθ,y=sinθ,
原式=(2+cosθ)2+sin2θ+2(2+cosθ)-4sinθ=9-2(2sinθ+3cosθ)
生8:本题也可用数形结合,因为x2+y2+2x-4y=(x+1)2+(y-2)2-5,其中
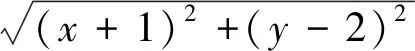
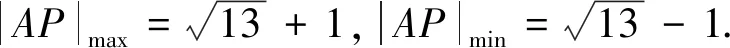
师:生8解法很有思想,数形结合,魅力无穷.
生9:刚才生7说x2+y2+2x-4y不是一次式,事实上,所求代数式可转化成一次式求解,故还可用判别式.
师:真的吗?说说你的发现.
生9: 由(x-2)2+y2=1,知x2+y2=4x-3,故x2+y2+2x-4y=6x-4y-3,可用判别式求解.
师:非常正确,转化成功,这个方法老师都没想到!让我们为他鼓掌!(掌声四起)
课堂小结:
本节课我们集中研究了在二次方程(一般不含xy项)限制性条件下,求代数式的最值问题.主要结论小结如下:
若被求代数式为线性(或可转化为线性),则可用“判别式”法求解,即“判别式”法是求解该问题的“通性通法”.
若已知条件可转化成圆或椭圆方程,则可考虑采用三角换元求解:若被求代数式又有明显的几何意义(斜率与距离)也可用数形结合求解.
3 感悟升华
3.1 “一轮后”复习也要重视“过程”
应该说随着课程改革的推进,教师在新授课的教学中,教师的教学观或多或少都发生了改变,探究活动,合作学习也常见于课堂.然而在高三一轮后复习备课的教学中,课堂再次被教师独霸,常见的教学是教师提前编写讲义,发给学生练习(或测试),教师结合学生错误多的地方进行重点订正.如此简单随意的教学,把习题课变成订正课,很难保证复习效率.即便在重点题型讲解上,也只是在炒剩饭,突出表现在以下两方面:一是对同一个题目采取一题多解,各种解法平行推进,以教师的讲解代替学生的思维,再以类似题进行固化的训练.然而一旦题目稍有变化,学生便感到“十八般武艺,样样不通”,教学的效果大打折扣.二是未能很好地将相关知识点进行“串联”,形成有机的整体,造成学生认知上的困难,学生的能力并未真正提高.本节课从一个简单而又不失经典的题目入手,全方位展示该题的多种解法,每一种解法都不是教师给出,而是由学生根据提议和结论,不断进行升级与改造,充分给学生时间,做足“过程”.为了进一步让学生逐个感悟到各解法的适用对象,课堂上将原题进行适当的变式,制造冲突,让学生时刻处于兴奋状态,让复习课也充满新鲜感.
“灌输”虽然也可以让学生获得知识,但失去了直觉、感悟和乐趣;而关注“过程”的教学在让学生获得知识的同时,却在发展着学生的思维,感受着数学的魅力,在生命层次上体验学习的乐趣,感悟数学的教育价值.
3.2 “一轮后”复习更要突出通法
本节课的题目引例虽然简单,但方法多样,倘若不慎,会让学生有“钱多不知如何花之感”.为此,在后续的教学安排中,不断变化条件与问题,最终让学生体会到“判别式法与“三角换元”作为解决此类问题的“通性通法”的威力与“魅力”!虽然问题较多,但由于问题设计条理清晰、层次清楚、设问自然,会有“忽如一夜春风来”的顿悟.
诚然,“通法”不能由教师简单地告知,而应当让学生去亲自体验与感悟.本节课教师似乎没有给学生任何解题“妙招”,而只是在追问学生“你是怎样想的”“还有什么想法”“为什么不能这样想”“为什么可以这样想”这些追问其实引导学生挖掘精彩背后的“通法”之源,充分暴露学生的思维过程,加深学生对知识的理解和运用,用“火热的思考”去替代“冰冷的美丽”,从而提升学生思维的品质.
3.3 学生是“一轮后”最具活力的资源
在高三复习后期(一轮复习已结束),学生对高中数学知识体系、思维方法都有了较系统的掌握.加之,他们对同一个问题思考角度不同,一定会带来不同的解题策略与方法,正所谓“众人拾柴火焰高”.在教学中,教师应注重对课堂最具活动的资源——学生的开发.如教师可以通过设置恰当的情境,让学生去探索、讨论、讲解,对于同一个问题,引导学生从多个角度去分析探究,鼓励一题多解;对于同一类问题,引导学生从中抽象概括出本质属性,总结规律和方法,强化通性通法,最终提升学生的解决问题的能力.

