一道抽象函数题的解法思考与改编*

福建省泉州市第七中学(362000) 黄永生 林志敏 杨 丹

1.试题呈现

(A)有极大值，无极小值

(B)有极小值，无极大值

(C)既有极大值又有极小值

(D)既无极大值也无极小值

2.思路分析与解答

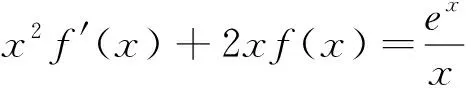
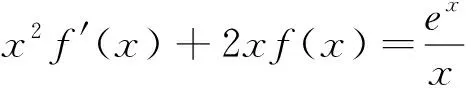
3.解法思考

(1)根据求导法则，对已知条件作变形，构造一个与原函数f(x)相关的g(x)；

(2)根据构造的g(x)，对已知条件作变形，构造一个与导函数f′(x)相关的h(x)；

(3)对含有g(x)和h(x)的等式两边求导，通过研究h(x)的最值，判定f′(x)的符号.

4.试题改编

(A)有极大值，无极小值

(B)有极小值，无极大值

(C)既有极大值也有极小值

(D)既无极大值也无极小值

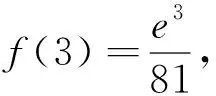
改编2 定义在(0,+∞)的函数f(x)的导函数是f′(x)，且满足f′(x)-f(x)=e2xlnx，f(1)=0，则f(x)( ).

(A)单调递增 (B)单调递减

(C)最大值为0 (D)最小值为0

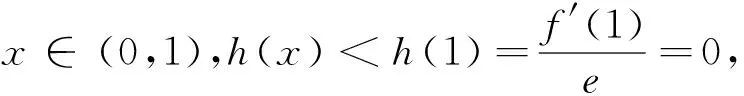
(A)f(x)在(0,+∞)单调递减

(B)f(x)在(0,+∞)单调递增

(C)f(x)在(0,+∞)上有极大值

(D)f(x)在(0,+∞)上有极小值

解答：在x2f′(x)+xf(x)=lnx中令x=e，得到f′(e)=0.

解答：由改编3解答可知f(x)在(0,+∞)单调递减，不等式f(x+1)-f(e+1)>x-e等价于f(x+1)-(x+1)>f(e+1)-(e+1).令g(x)=f(x)-x，则g(x)在(0,+∞)单调递减.不等式g(x+1)>g(e+1)等价于0