尖锐特征曲面点云模型各向异性邻域搜索
袁小翠 陈华伟
1(南昌工程学院江西精密驱动与控制重点实验室 江西 南昌 330099)2(贵州师范大学机械与电气工程学院 贵州 贵阳 550025)
0 引 言
三维扫描仪可以快速获取物体表面的三维信息,对三维点云数据处理可以实现曲面重建和产品再制造等应用。然而,三维扫描仪获取的数据一般只有三维坐标信息,无任何拓扑结构,点云数据处理时需要以点云的邻域为基础。点云邻域的准确性直接影响点云处理结果,如法向量估计、去噪和曲面重建等。
点云数据处理一般基于点云的k邻域。对任意点pi求其k邻域最直接的方法是计算该点与其他数据点的欧氏距离,取距离最近的k个点。然而,这种方法计算量大、效率低。为了提高计算效率,提出了许多快速邻域搜索算法。这些方法可以大致分为四类:多步递归法,并行法,栅格法(空间划分法)和数据重组算法[1],栅格法和数据重组法是比较常用的点云邻域搜索方法。
栅格法[2-5]计算邻域的思路是:对点云模型构建最大包围盒,对包围盒进行空间划分得到八个子立方体,再对这八个立方体进行递归划分直到子立方体不包含点云或者立方体的边长小于给定阈值。对任意点在其周围26个子立方体中搜索得到k邻域。文献[2-3]利用栅格法搜索邻域对曲面进行重建和提取点云模型空洞。文献[6]利用子块扩张方法避免搜索相邻子空间,但是该方法只适合规则点云。文献[4]解决了栅格法对大规模点云数据k邻域搜索效率低和分块不均匀的问题。
数据重组方法[1,7-10]主要是将数据划分为树状结构,它将整个数据集划分为多级子空间,这些子空间根据递归分裂规则用于构建树节点。因此,分裂规则决定了这些算法的搜索效率。例如,Cell树[8]通过将数据空间划分为大小相等的立方单元,从而构建了Cell树。VP树[9]通过划分数据空间建立二进制数。KD树[10]采用树节点来存储分区数据空间,从而缩小搜索范围。基于KD树的邻域搜索方法速度快,可以用于任何无规则点云,广泛应用于点云数据处理中。
以上点云邻域搜索方法主要专注于如何提高邻域构建算法效率,忽略了邻域的准确性。对于光滑曲面,点云k邻域可以比较准确地描述局部曲面信息,进而准确计算点云的相关信息,如点云微分信息和曲面重建等。但是,当点云处于高曲率区域,或者点云位于多个不连续曲面交界区域,这些方法计算得到的点云邻域位于多个不同连续曲面上。点云处理基于这种邻域容易造成严重的处理误差或者丢失曲面的细节信息,针对这些问题,提出各向异性邻域搜索方法。
1 邻域搜索方法
1.1 法矢估计及特征点检测
法向量估计的目的是将特征点的k邻域映射到高斯球形成多个独立的数据簇。一般利用点云的邻域拟合点云的切平面,切平面对应的法向量为点云的法向量。当点云模型处处光滑,通过邻域拟合的切平面法向量能准备描述点云的法向量。当点云处于高曲率区域,点云邻域位于多个不连续曲面上,拟合的切平面不准确,法向量被平滑。邻域拟合法估计法向量在文献[11]中被首次提出,被称为主成分分析法PCA(Principal Component Analysis),该方法计算快速,广泛应用于点云法向量估计。文献[12-13]改进了文献[11]的法向量估计方法,这些方法均能比较准确地估计尖锐特征模型的点云法向量,但是比较耗时。本文利用文献[11]方法粗略估计点云法矢,并对特征区域的法矢进行修正来获得较准确的点云法向量。

(1)
C被分解为三个特征向量:v2、v1、v0。三个特征向量对应的特征值分别为λ2、λ1、λ0,其中λ2≥λ1≥λ0。λ0对应的特征向量v0即为切平面法向量。
点的曲面变化表示为:
(2)
一般来说,当ωi=0时,表示点xi位于平面点,ωi值不为0,表示点xi处于非平坦区域,且ωi越大,表示点xi所处曲面越尖锐。因此,可以根据ωi值判断点xi的类型,即特征点和非特征点,如果ωi大于给定阈值Thresh,表示点xi为候选特征点。图1为经典模型Smooth-feature法矢和特征点检测结果,其中(c)为(b)中矩形框中折角面的放大图。灰色区域点表示检测的特征点,线条表示法向量。

(a) Smooth-feature模型 (b) 点云法向量

(c) 局部区域法矢 (d) 特征点图1 Smooth-feature模型法向量及其特征点
为了快速得到准确法向量,用平坦区域准确的法矢修正特征点的法矢。本文采用前期研究工作——邻域迭代加权法[14]修正特征点的法向量,特征点法矢修正表示为:
(3)
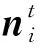
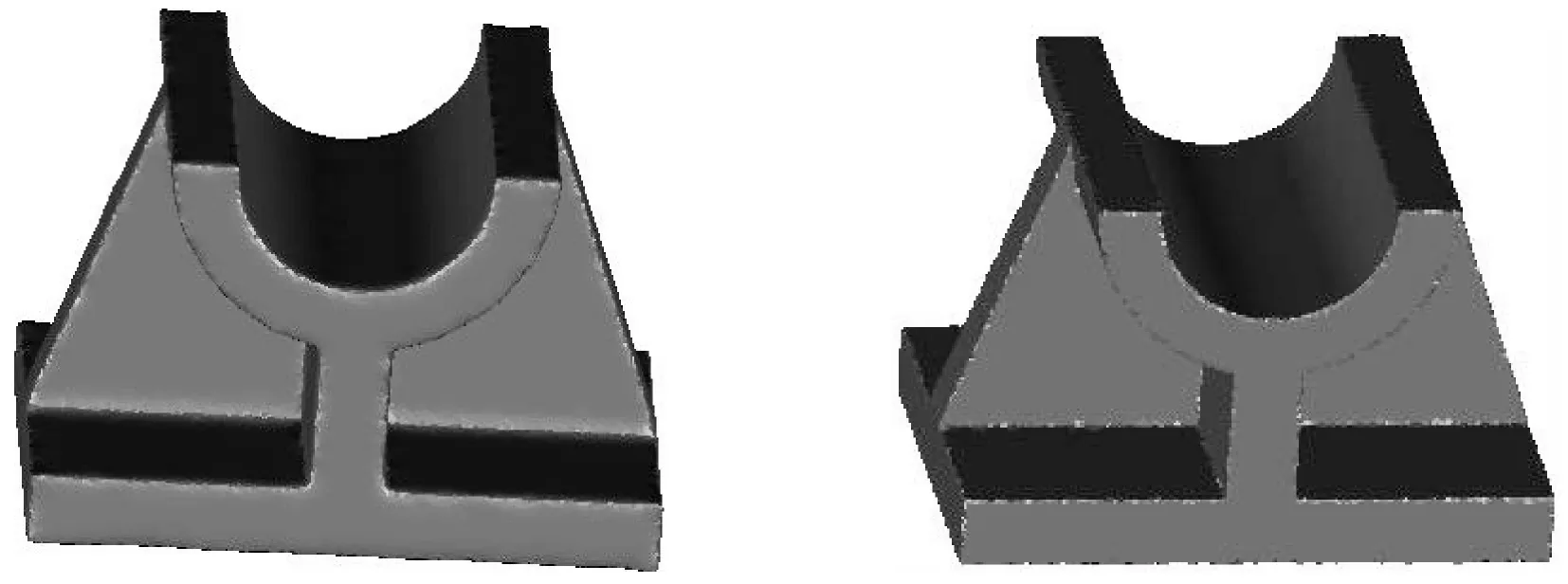
式中:σd、σn分别是距离带宽和法向偏差带宽,一般都取0.2,即σd=σn=0.2。
图2是法向量修正结果,图2(a)为Fandisk PCA方法估算得到的法向量,经过3次迭代(t=3)后修正结果如图2(b)所示,可以看出修正后的法向量几乎垂直所对应的局部曲面。

(a) PCA方法估计的法向量 (b) 修正后的法向量图2 Fandisk点云模型法向量修正结果
1.2 各向同性邻域分割
点云高斯映射[15]的目的是将特征点的各向同性邻域映射到高斯球上形成不同的数据簇。
高斯映射的特点:如果点云模型是一连通的平面,则该连通平面上的点云映射为高斯球上的一点;反之,如果点云模型的高斯图为高斯球上的一点,则该点云模型为一平面[15]。然而,估算的点云法向量与标准法向量总是存在一定的偏差,所以连通平面的点云映射为高斯球上密集的一个数据簇。
若估算的点云法矢比较准确,在局部区域连续曲面的法矢接近平行,该区域的点云高斯映射时形成一个密集分布的数据簇。若局部区域曲面不连续,不同曲面间的法矢夹角较大,高斯映射时形成多个数据簇,且数据簇的个数与曲面的个数一致。图3 (a)是由三个连续曲面相交形成的转角曲面模型,估算的法矢如图3(b)所示,斯映射示意图如图3(c)所示。局部区域不连续曲面的越尖锐,高斯球上不同数据簇的距离越远。

(a) 转角曲面点云 (b) 点云法向量 (c) 高斯图图3 特征区域高斯映射示意图
将特征点的Kb(一般Kb=3k)邻域映射到高斯球,在高斯球上形成不同的数据簇,再对高斯球上的数据簇聚类分割,将数据簇分为多个独立的子类,各子类对应不同连续曲面上的点云,即特征点的各向同性邻域被分割为多个子邻域,且各子邻域各向异性。因为无法确知特征点的各向同性邻域包含的各向异性子邻域的个数,所以需要用无参聚类分割法对高斯球上的数据分类。层次聚类和均值漂移算法是两种常用的无参聚类法,对特征空间中的样本点进行聚类时,无需指定聚类数目。均值漂移法对高斯球上的数据分割时容易产生多个聚类数目,每个类包含的点的个数少,使聚类结果不准确,因而,本文采用层次聚类法对数据分类。
假设特征点xi的Kb邻域组成的数据集合为:Psub={xi,i=1,2,…,Kb},则高斯球上的数据集表示为:
G(Psub)={g(x),x∈Psub}={ni,i=1,2,…,Kb}
式中:g(x)为点x的法向量,ni为点集Psub中第i个点的法向量,经过高斯映射后为高斯球上的第i个点。层次聚类分为凝聚和分裂聚类,本文采用凝聚层次聚类,该方法对数据样本聚类时将每个点作为一个单独的数据簇,合并这些原子数据簇为越来越大的簇,直到满足终止条件,且以平均距离为度量准则合并数据。簇间平均距离Dc表示为:
(4)
式中:|C1|、|C2|分别表示类C1、C2点的数量。d(ni,nj)为高斯球上ni、nj间的欧氏距离。且:
d(ni,nj)=2(1-〈nix,niy〉)
高斯球上点ni、nj的值为一行三列的单位向量,因此〈nix,niy〉表示单位法向量的内积nix、niy,当高斯球上的欧式距离小于T时合并为同类,即,样本数据的距离小于T=2(1-cosθ)时合并为同类数据簇,θ为法向量的夹角。高斯球上聚类结果对应为特征点k邻域点云分割结果,选取包含数据点最多的一个聚类对应的点云为所求邻域。
2 实验结果与分析
2.1 参数选择
本文点云邻域搜索算法中有4个参数需要用户设定(其他参数均为默认值),分别为特征点检测阈值Thresh、点云的KD树邻域的k值、特征点Kb邻域和层次聚类合并阈值θ。
(1)Thresh需要用户设定,参考值为0.01。
(2) 建立KD树,由用户选取点云的k邻域,当点云为平坦点,k邻域即为点云的各向异性邻域。
(3)Kb是特征点进行高斯映射的邻域,需要将Kb邻域分割来获得最优邻域,Kb的大小与k有关,本文取Kb=3k。因为特征点至少是两个曲面的交叉形成,为了使特征点的邻域大小与平坦点的邻域尽可能一致,需要根据曲面的复杂度来设定Kb值。例如,若点云的特征点由两个以上曲面交叉形成,可以取Kb=2k,若点云的特征点由三个以上曲面交叉形成,可以取Kb=3k,依次类推,本文默认取Kb=3k,且k=16。
(4)θ为高斯球上法向量夹角,当高斯球上两点的距离小于2(1-cosθ)时合并为同类数据簇。θ值影响各向同性邻域被分割为子邻域的个数。当点云及其邻域为平坦点,点云法向量接近平行,法向量之间的夹角比较小,因而,平坦区域点云邻域映射为高斯球上一个密集分布的数据簇。当两点的法向量夹角比较大,这两点一般来自两片不同的连续曲面,而且不连续曲面的特征区域的曲面越尖锐,法向量之间的夹角越大,即高斯球上的距离越大。当θ设为较小的值,特征点的各向同性邻域被分割为许多个小的各向异性邻域,当θ设为较大值,被分割后的邻域仍然是各向同性。文献[12-13]在测量估算法向量准确性时,计算标准法向量与测量法向量的夹角,当两者的夹角小于10°时认为该点为平坦点;当两者的夹角大于10°时,认为该点为特征点。考虑到估算的点云模型法向量与标准法向量存在一定的偏差,并受文献[12-13]的启发,本文将θ值设为10°,即当高斯球上簇与簇之间或者点与点之间的距离小于0.173(T=0.173)时合并为同类。
2.2 点云邻域应用
为了验证算法的有效性,对所求点云邻域进行实例验证,并且将本文搜索的邻域和其他方法搜索的邻域进行比较,如KD树[8]和栅格[4]邻域。采用C++语言编程在Microsoft visual studio 2015上实现点云邻域搜索和其他相关算法。由于点云的邻域难以直接可视化,本文将点云的邻域进行实例应用,即将不同邻域用于点云数据处理中,如点云法矢估计、点云去噪等。比较过程中除了输入的点云邻域不同,同一应用中的各个参数均相同。
2.2.1 邻域在法向量估算中的应用
邻域拟合法准确估计法向量的前提是用来拟合切平面的邻域来自同一片连续的曲面上。将KD树、栅格法和本文方法搜索得到邻域采用最小二乘法分别拟合切平面。基于几种不同邻域对八面体和经典的Fandisk点云模型估算点云法向量,法向量可视化结果如图4、图5所示。为了便于观察,对点云模型三角化显示,并且将法向量调整为一致方向,大小归一化。图4、图5中的(b-d)是几种邻域应用比较结果。栅格法和KD树法搜索到的邻域在平坦区域可以比较准确地拟合点云对应的切平面,从而估算的法向量比较准确。然而,在特征区域,特征点的邻域位于不同的连续曲面上,拟合的切平面不准确,从而法向量不准确。本文方法搜索得到的邻域在平坦区域即为KD树搜索的邻域,在特征区域特征点的各向同性邻域被分割,得到的是各向异性邻域,从而拟合的切平面比较准确,估算的法向量几乎垂直点云所在的局部曲面,如图4(d)、图5(d)所示。

(a) 八面体三角化模型(b) KD树邻域

(c) 栅格邻域 (d) 本文方法邻域图4 基于不同邻域八面体点云法向量估计结果比较

(a) Fandisk三角化模型 (b) KD树邻域

(c) 栅格邻域 (d) 本文方法邻域图5 基于不同邻域Fandisk模型法向量估计结果比较
2.2.2 邻域在点云去噪中的应用
双边滤波去噪法在去噪的同时能够比较有效地保留点云模型的尖锐特征,但是需要比较准确的点云法矢和点云邻域。双边滤波去噪法最早被用于特征保持的二维图像去噪,Fleishman等将双边滤波方法引入到三维网格光顺[16],该算法也同样适用于离散点云去噪。
双边滤波方法定义为:
x′=x+dn
(5)
式中,x为原始点云,x′为滤波后的点云,n为法向量,d为双边滤波因子,且:
(6)

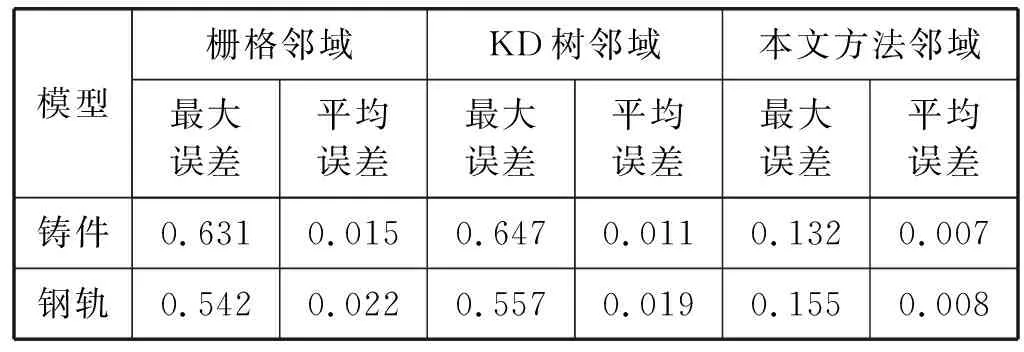
基于不同邻域对铸件和钢轨点云双边滤波去噪,此时Nb(x)分别表示KD树邻域、栅格邻域和本文方法所求邻域。基于三种不同邻域的双边滤波去噪结果如图6、图7所示。图6、图7两种点云模型都包含了非常明显的尖锐边界特征(多个不连续曲面交界处),为了突出去噪效果,对无噪声模型添加不同程度的噪声,对噪声点云去噪,并计算去噪产生的处理误差。图6、图7的(e-f)分别是基于三种不同邻域去噪结果。表1展示了基于三种不同邻域双边滤波器去噪的误差。由图6、图7和表1可知,基于本文方法的邻域去噪产生的误差最小,并且特征保留效果更好。

(a) 噪声点云数据 (b) 无噪声模型

(c) 加噪模型 (d) 栅格邻域
(e) KD树邻域 (f) 本文方法邻域图6 基于不同邻域铸件点云模型去噪结果

(a) 噪声点云数据 (b) 无噪声模型

(c) 加噪模型 (d) 栅格邻域

(e) KD树邻域 (f) 各向异性邻域图7 基于不同邻域钢轨点云模型去噪结果
2.3 不同邻域搜索方法耗时分析
实验所用的计算机配置为Intel Core i7-6500,2.50 GHz CPU,16 GB内存。对Fandisk,八面体、铸件和钢轨点云模型进行邻域搜索,不同方法搜索邻域耗时比较如表2所示。当点云模型处处光滑,不包含特征点时本文方法所求邻域即为kd邻域。当点云模型包含特征点,需要对KD数构造的邻域进行分割,相比于栅格法和KD树方法,本文方法搜索邻域耗时最长。
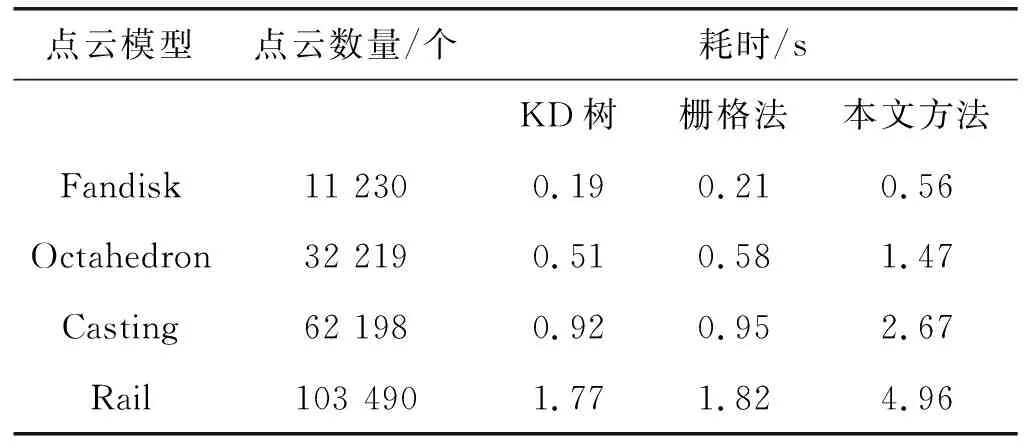
表2 点云邻域计算耗时比较
3 结 语
包含尖锐特征的点云模型邻域在特征区域点云邻域各向同性,本文对特征模型的各向异性搜索方法进行了研究。采用KD树方法快速搜索点云邻域,检测点云特征点寻找各向同性邻域,估算点云法向量,将各向同性邻域的法向量映射到高斯球,在高斯球上对各向同性邻域分割得到各向异性子邻域。将本文方法搜索的邻域与KD树和栅格法搜索的邻域进行了比较,本文方法搜索的邻域对点云数据处理(法向量估算和点云去噪)结果更准确,但是算法的复杂度更高,从而更耗时。在对复杂点云曲面重建或者去噪等领域,需要更好地保留原始点云模型的尖锐特征时可以采用本文方法来搜索邻域。本文算法有多个参数需要用户设定,今后工作中将在自适应和计算效率方面对点云邻域深入探讨。

