超声速栅格舵/弹身干扰特性数值模拟与试验研究

李永红，杨晓娟，陈建中，贾巍

(中国空气动力研究与发展中心，绵阳621000）

栅格舵作为一种特殊的气动控制面，由外部框架和内部若干栅格布置而成的一个空间多升力面系统，与传统的平板舵相比，栅格舵有其固有的优点［1-2］，体现在：①弦长较小，翼面上的压力中心距铰链轴很近且受迎角变化影响较小，因此舵面铰链力矩较小，降低了对作动装置的要求，允许采用较轻和较小的转向机构；②便于折叠，在不需要翼面时可以贴在主体表面，而不影响主体的外形，减小了栅格舵布局的空间体积；③栅格舵的流动分离晚于平板舵，具有不同于平板舵的失速特性，有利于在大迎角下保持升力［3-7］，对于提高导弹的最大可用过载、增强导弹的机动性和敏捷性，以及导弹的制导与防控具有重要的意义。

自1985年开始美国航空与导弹研究与发展中心对栅格舵布局就展开了相关研究［8-11］，特别是近年来国内外学者在减小超声速栅格舵阻力方面开展了大量的研究工作并取得了一定的进展［12-13］。然而，在栅格舵风洞试验中仍面临着较多的问题，比较突出的是在现有风洞条件下栅格舵按照风洞尺寸对弹体长度、堵塞度等要求进行缩比后，栅格舵翼元宽度和格壁厚度都较小，导致模型加工、检验困难，也可能无法满足风洞试验对模型强度的要求，造成试验无法开展，或即使能够加工，但由于气流的黏性作用，较小的格宽也会引起格壁通道内的非正常壅塞，从而导致气动力模拟失真。在这种情况下，将栅格舵和弹体按照不同缩比分开进行风洞试验，再将数据按照一定方法进行叠加得到全弹的气动特性成为获取栅格舵弹身组合体气动特性的一种思路。然而在开展这种方法研究之前，有必要开展弹身对栅格舵布局的干扰特性研究。因为与常规平板尾舵不同，在有迎角存在时，垂直安装在弹身表面的2片栅格舵会产生一定的法向载荷，另外，垂直安装的栅格舵主要受弹体头部分离体涡的影响，水平安装的栅格舵主要受弹体上洗流的影响，所以不同安装位置的栅格舵的气动特性会有较大差异。为对比这种差异，并研究弹体对栅格舵气动特性的影响，本文基于数值模拟方法分析了弹身对不同安装位置栅格舵的扰流特性和载荷分布，研究了由单独栅格舵气动特性转换到存在弹身干扰时栅格舵气动特性的修正方法。同时在中国空气动力研究与发展中心高速空气动力研究所FL-21风洞中开展相关试验，获取了2种不同安装方式栅格舵试验数据差异，验证了洗流修正方法的可行性。

1 研究模型

在弹身干扰特性研究中采用典型旋成体弹身简化外形，长细比为11，头部采用半球体，栅格舵采用格数为4×4的正置蜂窝式布局，呈十字型安装在弹体尾部距底部端面一倍弹径处，图1为栅格舵/弹身组合体外形示意图。图中：l为导弹弹身长度；D为导弹弹身直径；C为栅格舵翼弦；H为栅格舵翼高；L为栅格舵翼展；h为翼稍舵面距弹身表面距离；h0为翼根舵面距弹身表面距离。栅格舵基本外形尺寸与弹身直径的比值如表1所示。

图1 栅格舵/弹身组合体外形示意图Fig.1 Sketch map of grid fins/missile body configuration

表1 栅格舵外形尺寸Table 1 Main dimensions of grid fins

2 数值方法与网格划分

控制方程采用雷诺平均的Navier-Stokes方程，采用有限体积法进行空间离散，空间无黏通量采用Roe格式进行离散，黏性通量采用二阶中心差分格式离散，时间项采用隐式LU-SGS方法求解。为了加快收敛速度，采用局部时间步长和多重网格技术。湍流模型是两方程k-ωSST模型。计算时采用基于弹身长度的雷诺数，马赫数Ma=2.0时，Re=8.75×107。

计算网格采用“三层次”分块对接生成思想，附面层第1层网格y+≈1，全弹网格量约为1 100万。栅格舵/弹身组合体网络拓扑结构如图2所示。在网格的生成过程中，首先生成弹身组合体布局的网格；然后在弹身组合体网格的基础上，保持栅格舵物面及附面层网格不变，按照弹身组合体远场网格的划分规则生成单独栅格舵的远场网格，这样基本保持了单独栅格舵与存在弹身时栅格舵布局网格的一致性，降低了网格差异对气动特性的影响。

图2 栅格舵/弹身组合体网络拓扑结构Fig.2 Sketch map of topogical structure of grids for grid fins/missile booly configuration

3 数值计算结果与分析

在栅格舵和弹身组合体超声速气动特性计算中，采用一个简化模型来考虑弹体对栅格舵的气动干扰。图3为Ma=2.0，h0/D=0.375时，不存在弹体干扰的单独栅格舵法向力系数与存在弹身干扰时垂直以及水平安装的4片栅格舵法向力系数的对比。从图中可以直观地看出，弹体扰流对不同安装位置栅格舵的法向力特性的影响是显著的。尽管相对于传统平板舵布局来说，有迎角存在时，2片垂直栅格舵会产生一定的法向力，但是计算结果与单独栅格舵相比，上、下侧栅格舵的法向力都有不同程度的降低，即弹体的干扰是不利的，特别是上尾舵在迎角大于2°后，其法向力系数随迎角基本没有变化，主要是当迎角大于2°时，从弹体头部发出的体涡在到达栅格舵安装的弹体尾部位置时，其强度得到了增强，使得背风面栅格舵(上侧栅格舵）处在体涡的下洗流场中，当地迎角急剧降低。从图4所示纵向对称剖面马赫数及流线分布图中可以直观地看出，在来流迎角α=6°时，与迎风面尾舵相比，背风面尾舵附近的速度矢量方向几乎与弹体表面平行，即当地迎角几乎为0。定义当地迎角为

式中：un和vn分别为当地纵向和横向速度大小。

图5给出了Ma=2.0，h0/D=0.375，α=6°时栅格舵前缘剖面当地迎角云图。可以看出，受弹体涡下洗的影响，距离弹体越近，栅格舵元的当地迎角降低越严重，局部区域迎角降低为负值。处于迎风面尾舵(下侧尾舵）的当地迎角也有所降低，但相对所受干扰较小。

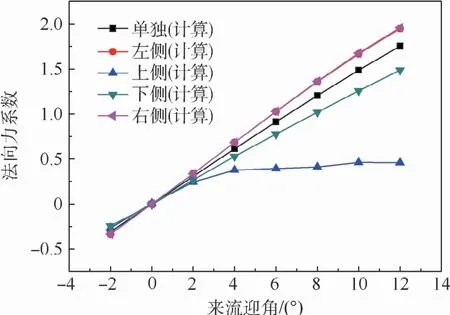
图3 弹身干扰对栅格舵法向力系数的影响(Ma=2.0，h0/D=0.375）Fig.3 Effect of missile body interference on normal force coefficients of grid fins(Ma=2.0，h0/D=0.375）

图4 纵向对称剖面马赫数及流线分布(Ma=2.0，α=6°，h0/D=0.375）Fig.4 Mach number and streamline distribution for longitudinal symmetrical profile(Ma=2.0，α=6°，h0/D=0.375）

对于水平安装的2片栅格舵而言，其法向力曲线的斜率要明显大于单独栅格舵布局，主要是由于弹体横向上洗流场增大了水平栅格舵的局部迎角。从图5可以看出，在来流迎角α=6°时，靠近弹体的栅格舵元附近的局部迎角接近8°，中部的栅格舵元附近的迎角也达到7.1°。

图5 栅格舵前缘剖面当地迎角云图(Ma=2.0，α=6°，h0/D=0.375）Fig.5 Cloud chart of local angle of attack for leading edge profile of grid fin(Ma=2.0，α=6°，h0/D=0.375）

文献［14］在研究弹体对栅格舵影响时，假定栅格舵的存在对弹体速度场没有影响，栅格舵处在弹身横向绕流的上洗流场中。弹身在栅格舵每个单元上引起的当地迎角为

式中：d为栅格舵某单元到圆心的距离；R为弹身的半径；θ为d与y轴夹角。对垂直或水平安装在弹身上的栅格舵，其法向力系数为

将式(2）代入式(5），即得

式中：A为修正系数，正号和负号分别对应水平和垂直安装在弹身上的栅格舵。基于沈遐龄和王丽丽［15］按照弹体的横向上洗理论，给出了修正系数的经验公式，即

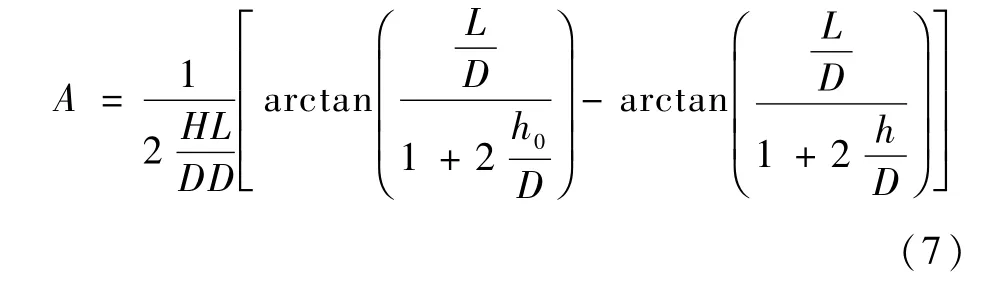
从而可得存在弹身干扰下的栅格舵的法向力系数为

基于式(8）将单独舵的法向力系数进行了洗流修正计算(计算结果用垂直修正，水平修正表征，分别代表垂直和水平栅格舵的修正结果），并与存在弹身洗流影响的栅格舵的法向力系数进行了对比，如图6所示，Ma=2.0，h0/D=0.375。可以看出，对于水平安装的栅格舵而言，利用洗流修正方法，单独舵修正以后的结果和弹舵一体的计算结果吻合较好，采用的修正方法是合理可信的，因此在无法进行栅格舵弹身组合体试验时，在已知单独栅格舵法向力的情况下，利用式(8）可以得到存在弹身干扰情况下水平安装的栅格舵的法向力特性。

图6 洗流修正结果与真实CFD计算结果对比(Ma=2.0，h0/D=0.375）Fig.6 Comparison of upward flow correction results and real CFD results(Ma=2.0，h0/D=0.375）

然而，对于垂直安装的栅格舵来说，迎风面栅格舵在来流迎角8°之前法向力系数可以得到较好的修正，随着来流迎角的增大存在过修正的趋势，特别是对于背风面栅格舵来讲，在来流迎角大于2°，按照式(8）所得的修正结果与实际计算结果相比明显偏大，因而对于垂直安装的迎风面和背风面栅格舵所受弹身的干扰影响是存在差异的，其法向力特性并不能由单一的修正因子进行修正。对于背风面栅格舵，在迎角大于2°时其法向力系数随来流迎角变化较小，且与单独栅格舵2°的法向力系数按照式(8）修正后的结果相当。

为进一步考察栅格舵与弹体表面距离的影响，将翼根舵面距弹身表面距离h0/D从原始的0.375降低到0.125。

图7为Ma=2.0，α=6°，h0/D=0.125时栅格舵前缘剖面当地迎角云图。可以看出，与图5相比，随着h0/D的降低，垂直安装的栅格舵受弹身干扰的影响增大，特别是背风面栅格舵，栅格舵元的当地迎角有显著降低，特别是距离弹体较近的两排栅格舵元的当地迎角降低为负值。图8为Ma=2.0，h0/D=0.125时，弹身干扰对栅格舵法向力系数的影响。栅格舵法向力系数的对比中可以看出，来流迎角大于2°时，背风面栅格舵的法向力系数随来流迎角的变化依然较小。

图7 栅格舵前缘剖面当地迎角云图(Ma=2.0，α=6°，h0/D=0.125）Fig.7 Cloud chart of local angle of attack for leading edge profile of grid fin(Ma=2.0，α=6°，h0/D=0.125）

图8 弹身干扰对栅格舵法向力系数的影响(Ma=2.0，h0/D=0.125）Fig.8 Effect of missile body interference on normal force coefficients of grid fins(Ma=2.0，h0/D=0.125）

从图9所示栅格舵法向力系数修正结果与计算值的对比中可以看出，用式(8）对水平尾舵的法向力修正仍然可以得到较为满意的结果。在迎角大于2°时背风面栅格舵的法向力系数与单独栅格舵来流迎角为2°的法向力系数按照式(8）修正后的结果也基本相当。

图9 洗流修正结果与真实CFD计算结果对比(Ma=2.0，h0/D=0.125）Fig.9 Comparison of upward flow correction results and real CFD results(Ma=2.0，h0/D=0.125）

因此，在超声速范围，基于单独栅格舵布局的法向力特性，通过弹体的横向上洗理论得出的修正公式可以较好得出水平安装的栅格舵以及垂直安装的迎风面栅格舵布局的法向力特性。在本文计算示例简化模型典型栅格舵外形尺寸条件下，对于垂直安装的背风面栅格舵布局，来流迎角大于2°时，其法向力系数可以用单独栅格舵来流迎角为2°的法向力系数修正后的结果进行赋值。

图10给出了Ma=2.0，h0/D=0.125时栅格舵轴向力系数的对比曲线。可以看出，无论是单独栅格舵布局还是存在弹身干扰的栅格舵布局，其轴向力随迎角的变化均较小，且弹身洗流对水平安装的栅格舵以及垂直安装的迎风面栅格舵布局的轴向力影响都较小，只是背风面栅格舵的轴向力相对于单独栅格舵布局来说降低了20%左右，此降低量约占全弹轴向力的1.5%，与法向力特性不同的是轴向力的差异与迎角的关系较小，主要是背风面气流受弹身的阻滞，能量损失严重，从栅格舵前缘剖面的马赫数云图(见图11）上来看，背风面栅格舵前缘的马赫数从来流的Ma=2.0降低到1.5左右，并随着离弹身距离的减小而进一步降低，而轴向力系数又是通过来流动压求得，因而轴向力会有明显的降低，但从量值以及对全弹轴向力贡献上来讲，可以不考虑弹身洗流对栅格舵轴向力的影响。

图10 弹身干扰对栅格舵轴向力系数的影响(Ma=2.0，h0/D=0.125）Fig.10 Effect of missile body interference on axial force coefficients of grid fins(Ma=2.0，h0/D=0.125）

图11 栅格舵前缘剖面当地马赫数云图(Ma=2.0，α=6°，h0/D=0.125）Fig.11 Cloud chart of local Mach number for leading edge profile of grid fin(Ma=2.0，α=6°，h0/D=0.125）

4 风洞试验验证

在中国空气动力研究与发展中心FL-21风洞(0.6 m×0.6 m跨超声速风洞）中进行了相关验证试验。由于模型尺寸和天平载荷匹配的限制，实际风洞试验模型尺寸在CFD计算数模基础上进行了调整，模型弹径增加到80 mm，栅格舵弦长截短减小到12 mm(即C/D=0.15），h0/D=0.125，其他参数基本保持不变。图12为单独栅格舵和弹身组合体模型在风洞中的试验照片。单独栅格舵模型与弹身组合体栅格舵模型几何尺寸相同。单独栅格舵模型通过半模杆式天平与风洞侧壁半模转窗相连，由半模杆式天平测量单独栅格舵的气动载荷。弹身组合体模型采用单支杆尾支撑方式固定于测力双支臂支架，由安装于弹体内部的六分量嵌套组合式铰链力矩天平测量栅格舵(测量舵）的气动载荷，通过滚转全弹的方式来实现不同位置栅格舵(测量舵）气动力和力矩的测量。试验马赫数为Ma=2.04，基于单位长度的试验雷诺数Re=2.38×107。

图12 风洞试验模型照片Fig.12 Photos of test models in wind tunnel

图13给出了Ma=2.0时不存在弹体干扰的单独栅格舵与存在弹身干扰时垂直以及水平安装栅格舵气动特性对比试验曲线。从图中可以看出，弹体扰流对不同安装位置栅格舵的法向力特性的影响是显著的，试验结果与计算结果规律基本一致。但上方栅格舵在来流迎角大于10°后，其法向力系数随来流迎角增大略趋于减小，同样是由于弹身洗流影响所致。

图13 弹身干扰对栅格舵法向力系数的影响Fig.13 Effect of missile body interference on normal force coefficients of grid fins

图14给出了Ma=2.0时栅格舵轴向力系数的对比试验曲线。无论是单独栅格舵布局还是存在弹身干扰的栅格舵，其轴向力系数随来流迎角的变化均较小，且弹身洗流对水平安装及垂直安装的栅格舵布局的轴向力影响都较小。

图14 弹身干扰对栅格舵轴向力系数的影响Fig.14 Effect of missile body interference on axial force coefficients of grid fins

同理，基于式(8）将单独栅格舵的法向力系数进行了洗流修正计算(计算结果用左侧修正，上侧修正，下侧修正表示），并与存在弹身洗流影响的栅格舵的法向力系数试验结果进行了对比，如图15所示。

从图15中可以看出，对于安装在弹体左侧(水平安装）的栅格舵而言，利用洗流修正方法，Ma=2.0时，单独栅格舵修正以后的结果和弹舵一体试验结果吻合很好，采用的修正方法是合理可信的，因此无法进行栅格舵弹身组合体试验时，在已知单独栅格舵法向力的情况下，利用式(8）可以得到存在弹身干扰情况下水平安装的栅格舵的法向力特性。对于安装在弹体上方(垂直安装）的栅格舵来说，栅格舵处于背风面，小来流迎角时法向力系数可以得到较好的修正，随着来流迎角增大，修正结果与试验结果相比明显偏大，存在过修的趋势，其法向力特性并不能由单一的修正因子进行修正。但对于安装在弹体下方(垂直安装）的栅格舵来说，来流舵处于迎风面，Ma=2.0时，按照式(8）修正后的结果与弹舵一体试验结果吻合很好。

图15 洗流修正结果与试验结果对比Fig.15 Comparison of upward flow correction results and test results

5 结 论

本文基于数值模拟方法分析了超声速条件下弹身对不同安装位置栅格舵干扰特性的影响，研究了栅格舵法向力、轴向力的修正方法，并通过风洞试验进行了验证，探讨了修正方法的可行性，得出如下结论：

1）有弹身存在时，垂直安装的栅格舵由于受弹体头部分离涡的影响，法向力系数较单独栅格舵有不同程度的降低，特别是背风面尾舵的法向力系数在迎角大于一定角度后随迎角变化较小时，其法向力系数可以用单独尾舵该角度下的法向力系数按照洗流影响修正后的结果进行赋值。迎风面尾舵的法向力系数可以通过单独栅格舵洗流修正结果得到。

2）有弹身存在时，水平安装的栅格舵由于受弹体上洗流的影响，法向力系数较单独栅格舵有明显增大，但是基本可以通过单独栅格舵洗流修正结果得到。

3）栅格舵轴向力受弹身干扰影响较小。

4）洗流修正方法是可行的，通过修正单独栅格舵气动系数并叠加到弹体从而得到全弹的气动特性，在工程上是适用的。