椭圆截面弹体斜侵彻金属靶体弹道研究*

魏海洋，张先锋，熊 玮，周婕群，刘 闯，冯晓伟

（1. 南京理工大学机械工程学院，江苏 南京 210094；2. 中国工程物理研究院总体工程研究所，四川 绵阳 621999）

相较于圆截面弹体，异型截面弹体具有平台适应性好、装填比大、抗弯强度高及可提高平台内部腔体空间利用率等优点。近年来，异型截面弹体侵彻问题已成为武器研发领域的研究热点。Woo研究了任意截面形状的空腔膨胀过程中的边界阻力分布特性，并由此得到了非圆截面弹体结构能够有效降低靶体侵彻阻力的结论。Bless开展了长方形截面杆体及圆截面杆体高速侵彻试验，对比分析了二者的侵彻效率，得出了在临界速度以下非对称截面弹体侵彻性能更优的结论。杜忠华等开展了圆截面、矩形截面、三角形截面3 类侵彻体侵彻半无限金属板的试验与理论研究，发现在3 类弹体截面比动能相等的情况下，侵彻效率由高到低分别为三角形截面弹体、矩形截面弹体及圆截面弹体。高光发等基于杜忠华等的试验结果，开展了相应的数值模拟工作，进一步验证了该结论。Partom 等开展了不同速度下旋转对称圆截面弹体和平面对称非圆截面弹体侵彻金属板的数值模拟研究。荣光等开展了正方形和正三角形截面结构弹体的高速垂直和斜侵彻金属靶板的试验研究，结果表明，相同速度下，两种变截面结构弹体的垂直侵彻深度相差不大，但正方形截面结构弹体斜侵彻的深度略大于三角形截面结构弹体。王文杰等开展了椭圆截面弹体侵彻半无限厚混凝土试验，基于局部相互作用理论及空腔膨胀理论，分析了椭圆截面弹体的侵彻阻力，建立了椭圆截面弹体侵彻深度计算模型。Dong 等、Zhang 等、刘子豪等、王浩等开展了椭圆截面弹体侵彻半无限厚混凝土试验，通过引入椭圆截面弹体头部形状因子对空腔膨胀理论进行修正，分析了弹体头部阻力变化规律，建立了椭圆截面弹体正侵彻深度模型，随后开展了椭圆截面弹体对多层钢板的侵彻破坏模式研究，分析了弹体侵彻过程中的弹道特性。

弹体在侵彻过程中偏离初始的速度方向而使得侵彻弹道弯曲、偏转是一个普遍的物理现象。试验结果表明，弹体侵彻混凝土、岩石、土壤、金属等靶体过程中均会受到多种因素的作用而发生弹体偏转现象。当前，Bernard 等、Warren 等、Fang 等、Kong 等、孔祥振等、Wei 等对侵彻弹道的研究多以圆截面弹体为主，且主要采用数值模拟以及试验研究手段，而针对侵彻弹道的理论研究工作开展较少。同时，关于椭圆截面弹体侵彻弹道研究工作的公开报道较少。

目前，关于异型截面弹体的设计包括多种截面形状，且以异型截面弹体对典型靶体的正侵彻研究为主。侵彻弹道研究则关注圆截面卵形弹体侵彻问题，尚未涉及椭圆截面弹体的侵彻弹道研究。本文中，以圆截面卵形弹体形状函数为基准设计椭圆截面弹体，开展椭圆截面弹体以不同撞击速度及倾角侵彻半无限2A12 铝合金靶体试验研究；同时，基于局部相互作用模型及空腔膨胀理论，建立弹体形状表征函数，发展椭圆截面弹体对半无限金属靶体的侵彻弹道模型，并结合试验数据验证模型的可靠性，分析椭圆长短轴之比、弹体绕轴旋转角度、弹体撞击速度对侵彻弹道的影响规律。

1 椭圆截面弹体侵彻弹道模型

弹体侵彻问题是一个复杂的动力学问题。为简化这一过程，本文中，假设弹体为刚性弹体，结合空腔膨胀阻力模型及局部相互作用理论，分析椭圆截面弹体斜侵彻过程中的阻力特性，建立椭圆截面弹体对半无限金属靶体的侵彻弹道模型。

1.1 椭圆截面弹体形状函数

基于局部相互作用理论，引入局部笛卡尔坐标系描述椭圆截面弹体形状，如图1 所示。图中为椭圆截面的短半轴长，为椭圆截面的长短轴之比（=1），为弹体头部长度，为弹体长度。图1 中以短半轴长为有效半径，其所对应的头部曲率半径为，以此获得椭圆截面弹体的等效曲径比为/2，同时，对椭圆截面长半轴进行放缩，使得椭圆截面弹体头部任意椭圆截面的长短轴之比恒定，其所对应的椭圆截面弹体头部曲线为椭圆弧，见图1。因此，椭圆截面弹体的头部形状可表示为：

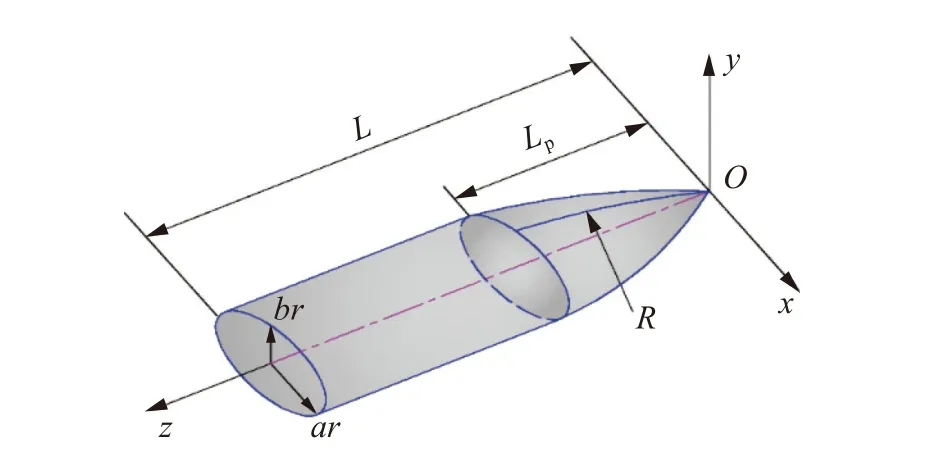
图1 椭圆弹体形状示意图Fig. 1 Schematic diagram of the elliptical cross-section projectile

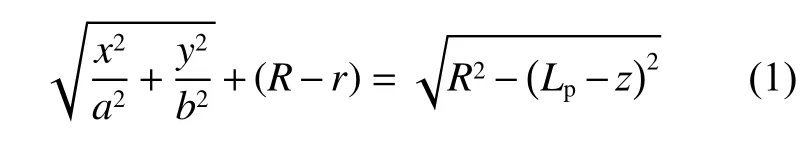
考虑弹体绕轴逆时针（从轴正向）旋转γ 角，且椭圆截面弹体为非旋转弹体。为便于分析计算，将弹体形状函数转换至柱坐标系下，因此，式(1)可改写为：

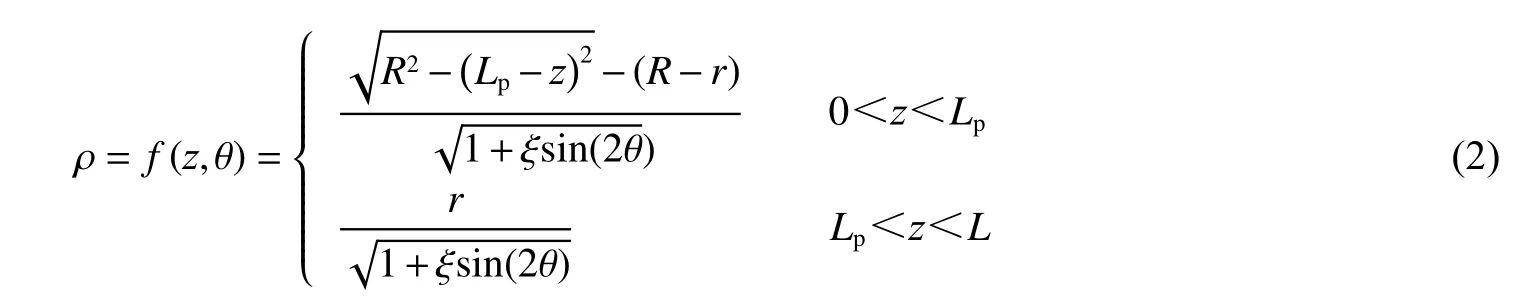
式中：(, θ)为椭圆截面弹体形状函数，ξ 为与弹体绕轴旋转角度γ 相关的因子，可表示为：

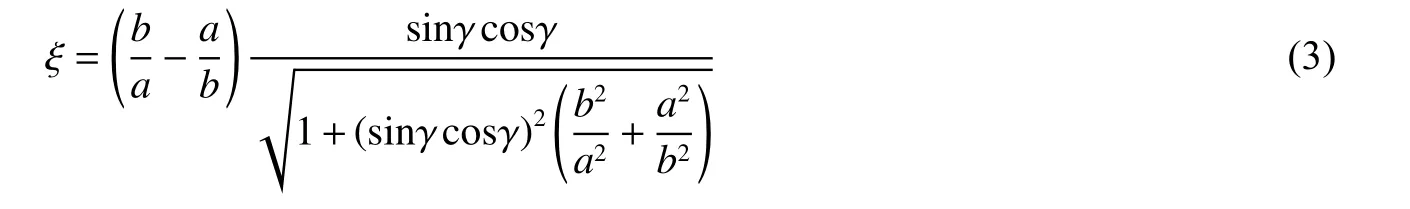
1.2 弹体侵彻阻力模型

Forrestal 等的研究表明，弹体在侵彻理想弹塑性应变硬化不可压缩材料过程中，其空腔膨胀阻力模型可表示为：

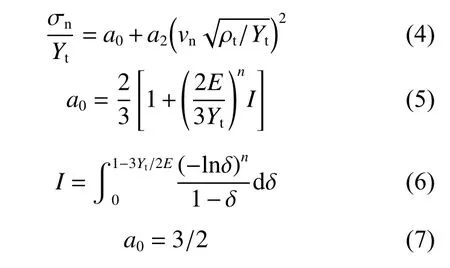
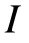
图2 为弹体侵彻初始条件分析示意图。图中为弹体初始撞击速度，θ为弹体在平面内的弹轴与速度方向夹角，即攻角；ψ为弹体在平面内的弹轴与速度方向夹角，即偏航角；v、v、v为初始撞击速度在局部坐标下沿、、轴方向的速度分量；α为弹体在平面内的初始倾角；β为弹体在平面内的初始倾角。为便于分析弹体侵彻弹道，在局部坐标系之外引入整体坐标系。其中，笛卡尔局部坐标系与整体坐标系间的转换关系可以表示为：

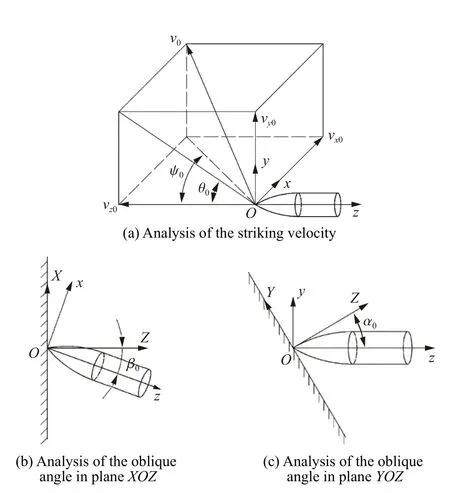
图2 侵彻初始条件分析Fig. 2 Analysis of the initial penetration conditions

式中：v、v、v分别为弹体在局部坐标系沿、、方向的平移速度分量，n、n、n分别表示弹体表面外法向向量在局部坐标系下沿、、方向的分量。

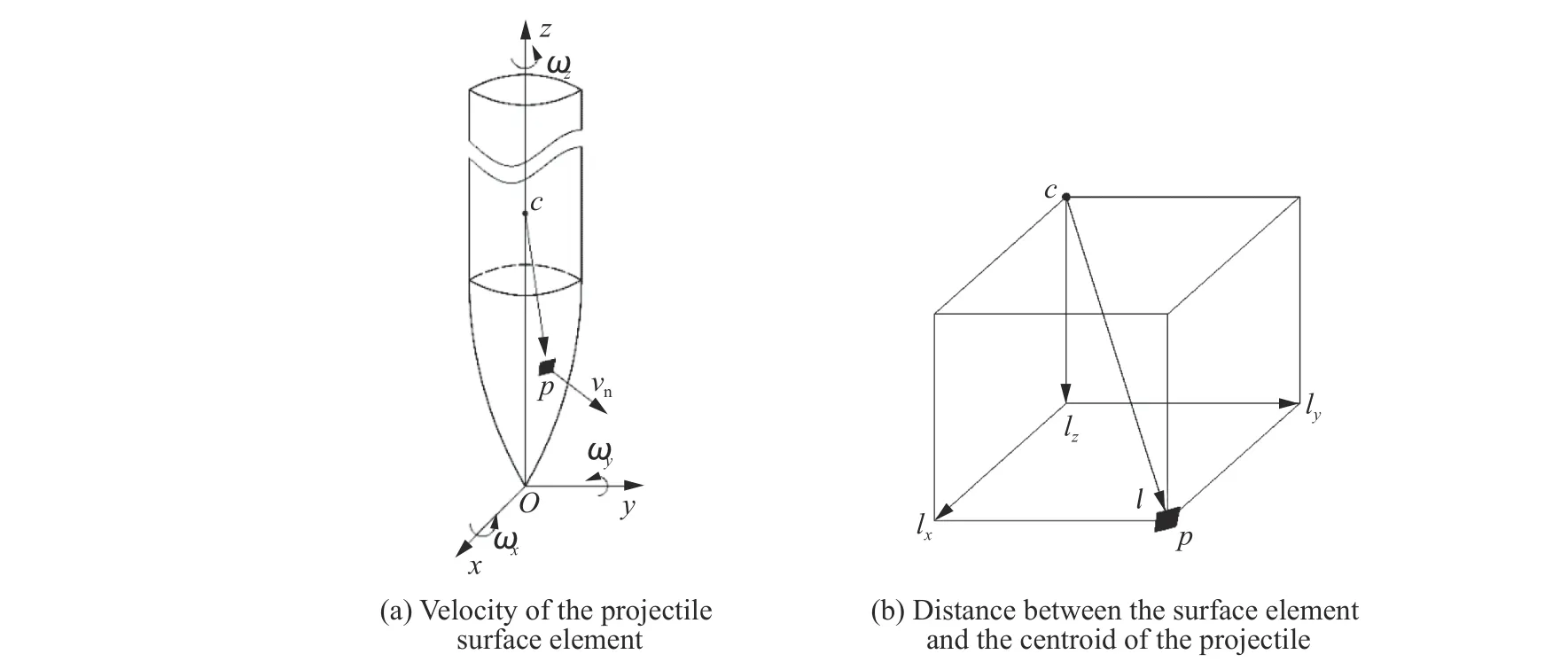
图3 弹体表面微元法向速度分析Fig. 3 Analysis of the outer normal velocity of surface elements of the projectile

图4 为局部坐标系下弹体斜侵彻过程中的阻力分析示意图。由图4 可知，弹体表面所受偏转力及力矩可表示为：

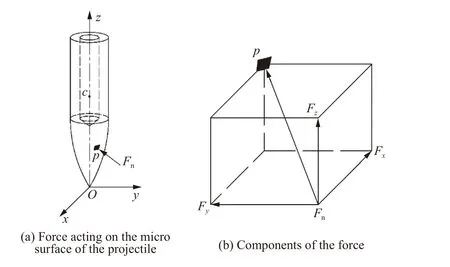
图4 弹体受力分析Fig. 4 Analyses of forces and moments acting on the projectile

式中：为弹体表面微元法向受力。有：

式中：Σ 为弹靶接触面积，d为弹体表面微元的微分形式。有：

因此，结合式(8)，即可将弹体在整体坐标系下的偏转力及力矩表示出来。

1.3 椭圆截面弹体侵彻半无限厚金属靶弹道模型

基于刚性弹体假设，弹体在局部坐标系下的空间运动方程为：

式中：为弹体质量，a、a、a分别为弹体沿、、方向的过载，J、J、J分别为弹体绕穿过质心的、、轴的转动惯量，η、η、η为弹体偏转角加速度。弹体在局部坐标系下的初始侵彻条件为：

式中：ω|、ω|、ω|为弹体偏转角速度分量初始条件，ω、ω、ω为弹体着靶前绕局部坐标系下、、轴的旋转速度。弹体整体坐标系下的侵彻初始条件可结合式(8)得到，同时弹体侵彻弹道亦可结合式(8)、式(14)～(17)得到。

2 椭圆截面弹体侵彻铝合金靶弹道试验

为研究椭圆截面弹体对半无限金属靶的侵彻弹道规律及验证侵彻弹道模型，基于14.5 mm弹道枪平台，开展了椭圆截面弹体以850～950 m/s撞击速度斜侵彻半无限金属靶试验。

2.1 试验弹体及靶体

图5 为试验椭圆截面弹体实物。图中，弹身处椭圆截面长轴长14.5 mm，短轴长9.0 mm，等效头部曲径比为5.6。弹体全长43.5 mm，质量为22.2 g。试验弹体由弹芯、底推组成。弹芯材料为30CrMnSiNi2A，密度为7.85 g/cm，热处理后HRC 硬度为42～45。为达到良好的闭气效果，底推材料选用铝合金，使弹芯在发射过程中与枪管配合紧密，保证弹体发射的稳定性，弹体结构质量参数见表1。

表1 弹体结构质量参数Table 1 Parameters of the projectile

图5 弹体实物Fig. 5 Photo of an elliptical cross-section projectile

图6 试验现场布局Fig. 6 Layout of the testing site

表2 2A12 铝合金力学性能参数Table 2 Parameters of the target material aluminum alloy 2A12

2.2 试验结果

共计开展3 发试验，弹体倾角分别为5°、10°、20°。图7 为弹体飞行姿态分析示意图。由图7 可知，弹体外弹道飞行特性较好。

图7 弹体飞行姿态分析Fig. 7 Analysis of the flight attitude of the projectile

弹体侵彻前和侵彻后的长度及质量分别为43.5 mm、22.2 g 和42.3 mm、21.2 g。因此，椭圆截面弹体斜侵彻过程可视为刚体侵彻。图8 为椭圆截面弹体在不同倾角及撞击速度下靶体的破坏结果。由图8可知，当弹体以较小角度侵彻靶体时，靶体表面变形呈花瓣状。同时，由于弹体截面为椭圆形，在着靶前弹体绕弹轴旋转一定角度，导致靶体表面孔洞与水平方向存在一定角度。当弹体斜侵彻时，由于弹靶相互作用而产生的非对称力，使得靶体表面孔洞一侧受到的挤压较另一侧更严重。随着弹体着靶倾角的增大，与弹体上表面接触的靶体材料逐渐由挤压转向崩落。

图8 靶体破坏结果Fig. 8 Damage patterns of the targets

图9 为不同倾角及撞击速度下弹体的侵彻弹道。由图9 可知，椭圆截面弹体侵彻弹道随着倾角的增大而更加不稳定，随着撞击速度的提升则趋向于稳定。同时，由图9(a)可知，尽管在试验前预设的倾角为0°，但是弹体的侵彻弹道仍然出现了弯曲偏转，通过高速摄像对弹体着靶姿态进行校核，弹体着靶角度为5°，使得弹道发生偏转。通过高速摄像系统观察及记录侵彻后靶体破坏结果，弹体侵彻试验结果见表3。表中：S、S、S分别为弹体在整体坐标系下沿、、方向的位移，α为弹体最终姿态角。

图9 侵彻弹道试验结果Fig. 9 Results of the penetration trajectories

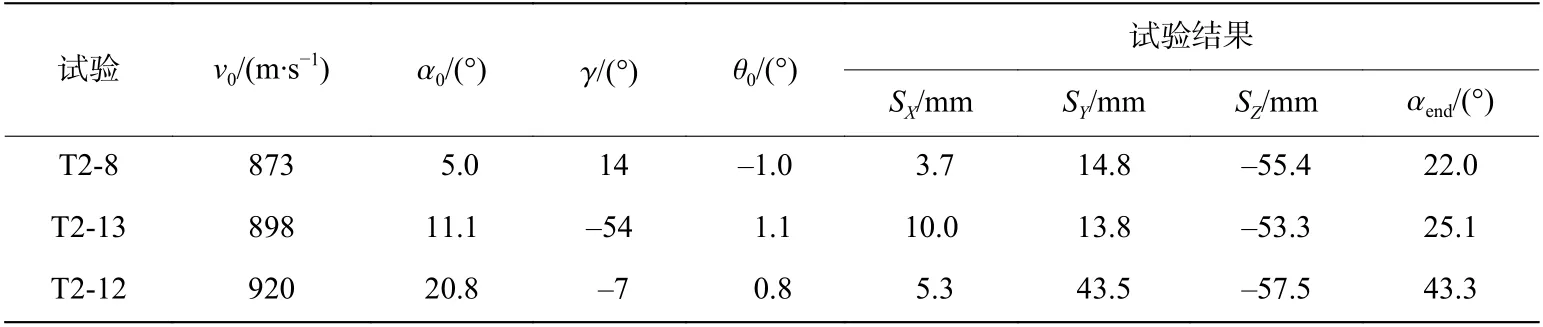
表3 弹体侵彻试验结果Table 3 Test results of the penetration trajectories

3 椭圆截面弹体侵彻弹道模型验证与讨论

3.1 模型验证

基于第2 节的理论公式，通过编写程序代入弹体形状函数及初始侵彻条件，求解出不同侵彻条件下椭圆截面弹体对半无限2A12 铝合金靶体的侵彻弹道，并与第2 节试验结果进行对比验证。图10 为不同侵彻条件下椭圆截面弹体侵彻弹道的计算结果与试验结果的对比。由于本模型未考虑靶体表面破坏如材料挤压、裂纹扩展等对侵彻弹道的影响，同时，弹体在平面内的攻角并未观测，因此，当弹体在平面的倾角为5°时，弹尖终点坐标S与试验结果相差较大，但是弹体在向的侵彻深度与试验结果接近。当弹体在平面的倾角为11.1°及20.8°时，弹尖终点坐标与试验结果吻合较好。表4 为弹体终点坐标计算结果与试验结果的对比。

表4 椭圆截面弹体终点坐标对比Table 4 Comparison of the final coordinates of the elliptic cross section projectiles

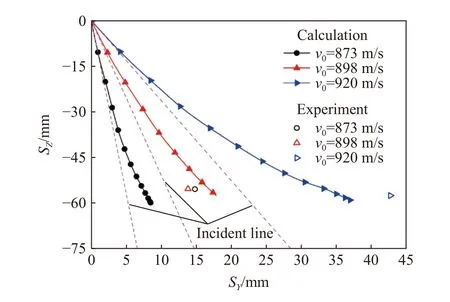
图10 椭圆截面弹体侵彻弹道Fig. 10 Penetration trajectories of the elliptic cross section projectiles

3.2 椭圆截面弹体侵彻弹道影响因素分析

基于椭圆截面弹体侵彻弹道模型，对影响弹体侵彻弹道的主要因素进行分析，包括弹体的长短轴之比，弹体绕弹轴旋转角度γ 以及弹体撞击速度。

3.2.1 弹体长短轴之比对侵彻弹道的影响分析

为研究椭圆截面弹体长短轴之比对侵彻弹道的影响规律，长短轴之比（=1）分别取1.0、1.2、1.4、1.6、1.8、2.0，并计算相应弹体的侵彻弹道。其中，当长短轴之比为1.0 时，弹体退化为尖卵形圆截面弹体。计算弹体结构质量参数如表5 所示。表中：1弹体为尖卵形圆截面弹体，2～6弹体为椭圆截面弹体，为弹体头部等效曲径比，为弹体质心至弹尖的距离。各弹体质量、弹体头部长度、弹体等效曲径比均保持一致。

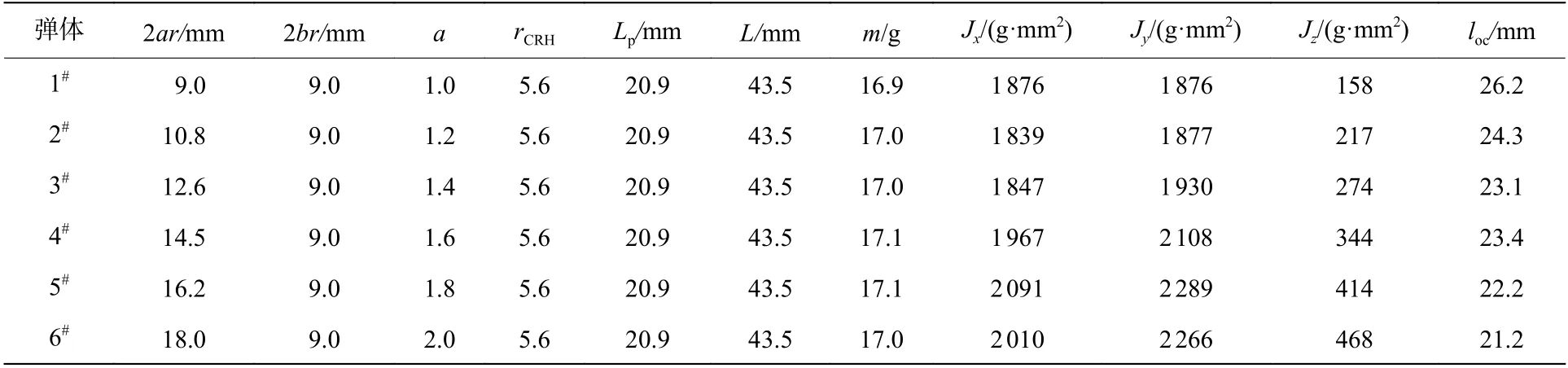
表5 计算弹体结构质量参数Table 5 Computational parameters of the projectiles

同时，为对比分析弹体的侵彻弹道，弹体的撞击速度均为900 m/s，平面内初始倾角为20°，其他初始侵彻条件均设为零。图11～12 分别为不同长短轴之比的椭圆截面弹体侵彻弹道、弹体姿态变化计算结果。从图中可以看出，当弹体绕轴旋转角度为0°时，椭圆截面弹体侵彻弹道稳定性随着长短轴之比的增大越来越差，同时，弹体长短轴之比的最优值为1.0。

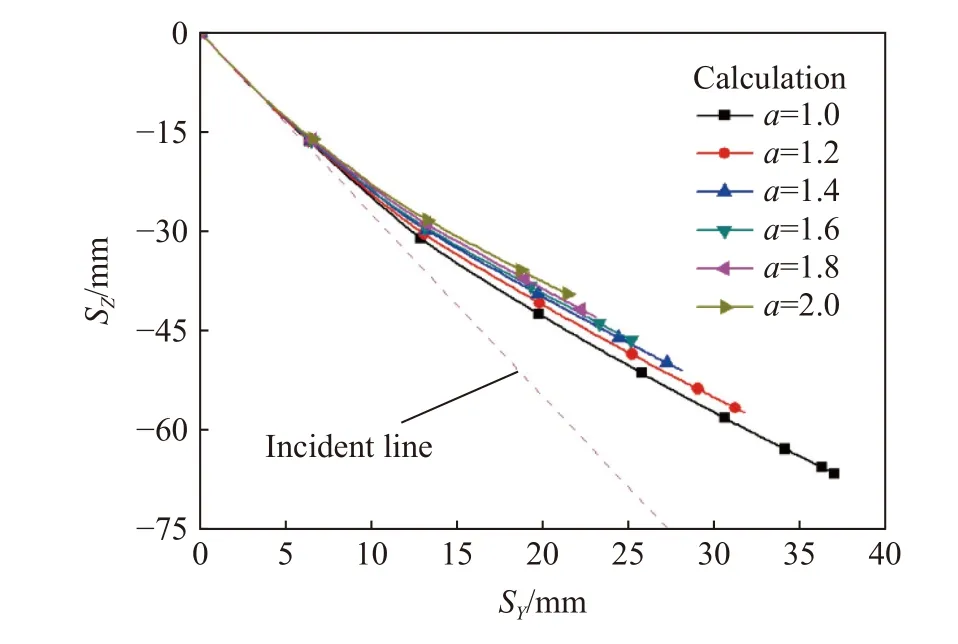
图11 γ=0°时不同弹体侵彻弹道计算结果Fig. 11 Calculation results of the penetration trajectories of various projectiles while γ is 0°

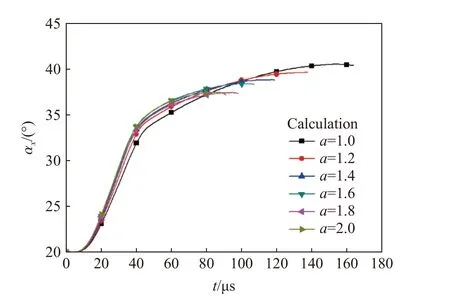
图12 γ=0°时不同弹体的姿态角变化Fig. 12 Time histories of the attitude angle αx of various projectiles while γ is 0°

3.2.2 弹体绕弹轴旋转角度对侵彻弹道的影响分析

为分析椭圆截面弹体绕轴旋转角度对侵彻弹道的影响规律，以表5 中的4弹体为弹体计算模型，计算弹体在900 m/s 撞击速度、20°倾角时的侵彻弹道。其中，弹体绕弹轴旋转角度γ 分别取0°、30°、60°、90°，如图13 所示。图14 为不同γ 角度下椭圆截面弹体侵彻弹道计算结果。由图14 可知，椭圆截面弹体侵彻弹道稳定性随着绕轴旋转角度的增大而变差。同时，根据计算结果，弹体在绕弹轴旋转角度γ 分别取0°、30°、60°、90°时，在方向上终点坐标分别为0、2.7、3.0、0 mm。由此可知，当椭圆截面弹体以一定的绕轴旋转角度侵彻靶体时，弹体的受力不再局限于平面，在平面内亦有分量。

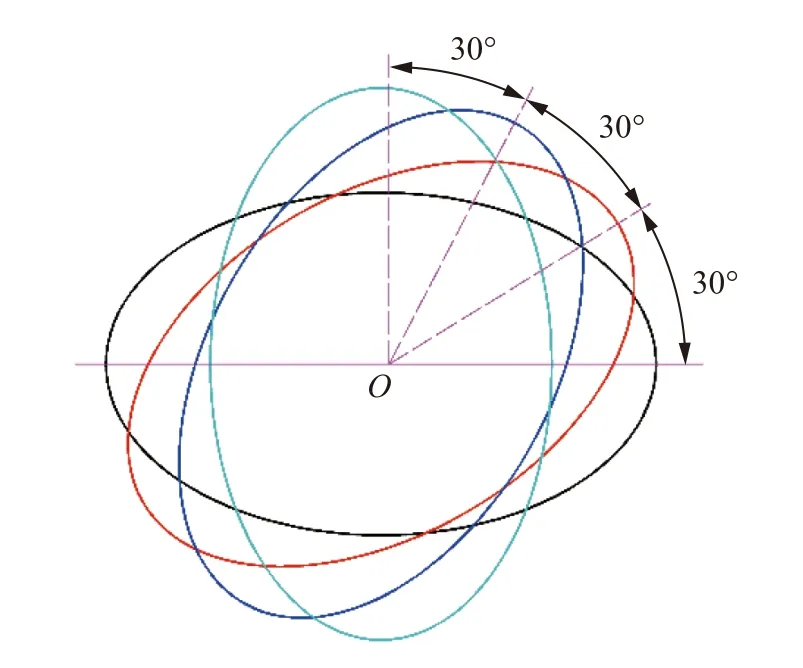
图13 弹体绕弹轴旋转示意图Fig. 13 Schematic diagraph of the projectilerotating around axis z

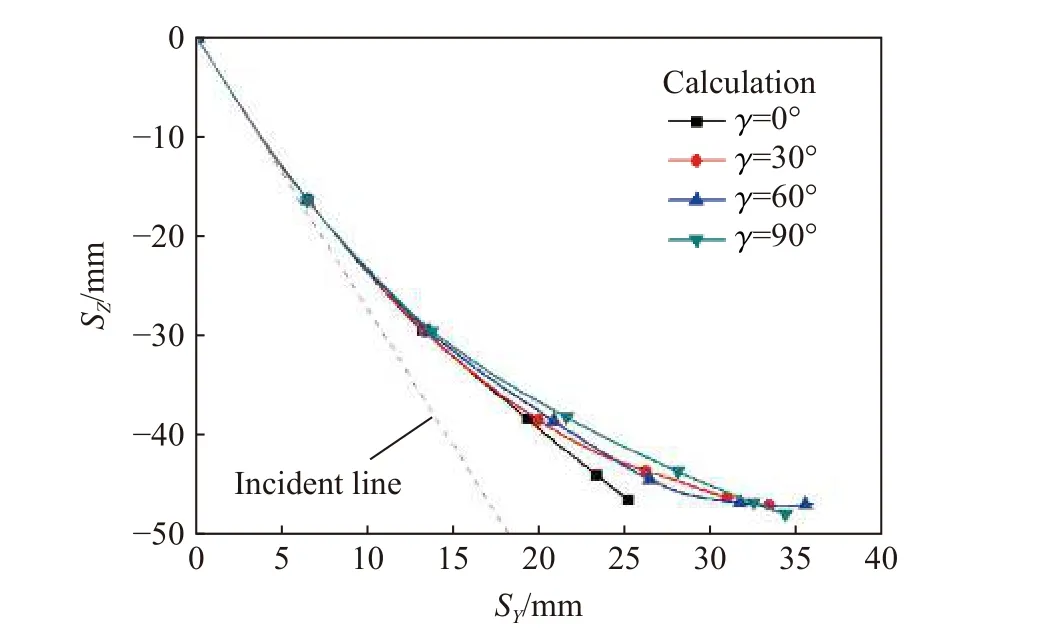
图14 不同γ 角下弹体侵彻弹道计算结果Fig. 14 Calculation results of penetration trajectories at different γ

图15 为不同γ 角度下弹体姿态角的变化曲线。由图15(a)可知，当β为0°时，侵彻初始条件α成为影响弹体侵彻弹道的主控因素。当γ 分别为0°、90°时，弹体在平面内的姿态角α的变化规律相同，但是γ 为0°时弹体的侵彻弹道比γ 为90°时的侵彻弹道稳定；当γ 分别为30°、60°时，弹体姿态角α 的变化说明弹体受力及力矩已变成空间向量，使得弹体侵彻弹道成为空间曲线。由图15(b)可知，当γ 分别为0°、90°时，弹体侵彻弹道落在平面内，而当γ 分别为30°、60°时，弹体侵彻弹道不再局限于平面内，而是成为复杂的空间曲线。

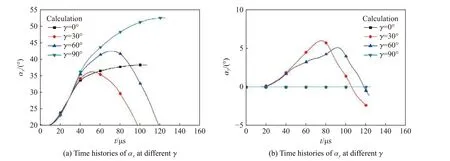
图15 不同γ 角度下弹体姿态角变化Fig. 15 Time histories of the attitude angle of projectiles under different γ

3.2.3 弹体撞击速度对侵彻弹道的影响分析

为分析椭圆截面弹体撞击速度对侵彻弹道的影响规律，以4弹体为计算模型，分别计算弹体以800、900、1000 m/s 的撞击速度、20°倾角下对铝合金靶体的侵彻弹道。其中，倾角位于平面内，弹体绕弹轴旋转角度γ 为0°。图16 和17 分别为不同撞击速度下弹体的侵彻弹道计算结果及弹体姿态角变化。从图中可知，随着弹体撞击速度的提升，弹体偏转角度变小，弹体侵彻弹道越趋于稳定。

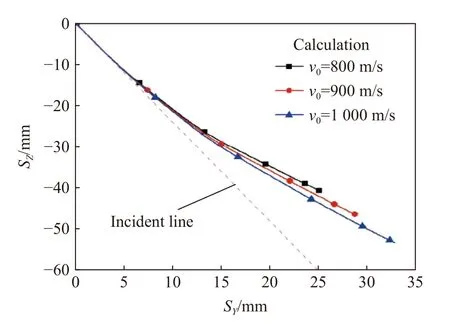
图16 不同v0 下弹体侵彻弹道计算结果Fig. 16 Calculation results of the penetration trajectories at different v0

图17 不同v0 下弹体姿态角变化Fig. 17 Time histories of the attitude angle at different v0

4 结 论

开展了0°、10°、20°倾角椭圆截面弹体在850～950 m/s 撞击速度范围内斜侵彻铝合金靶体试验，获得了椭圆截面弹体对半无限金属靶体的侵彻弹道。在此基础上，建立了椭圆截面弹体对半无限金属靶体的侵彻弹道模型，并结合试验结果验证了模型的有效性，主要结论如下。

（1）椭圆截面弹体长短轴之比对侵彻弹道有较显著影响。当长短轴之比为1.0 时，弹体退化为尖卵形圆截面弹体。椭圆截面弹体侵彻弹道稳定性随着长短轴之比的增大而变弱，最优长短轴之比为1.0，即尖卵形圆截面弹体。

（2）椭圆截面弹体绕弹轴旋转角度对侵彻弹道影响非常显著。当弹体绕弹轴旋转角度为0°、90°时，侵彻弹道可视为平面曲线，且旋转角度为0°时的侵彻弹道稳定性优于旋转角度为90°时的侵彻弹道；当旋转角度为30°、60°时，侵彻弹道则成为空间曲线，弹体受力及力矩变得更复杂，且在侵彻过程中弹体边侵彻边绕轴旋转，使得侵彻弹道更加不稳定。

（3）椭圆截面弹体撞击速度对侵彻弹道影响较小。当绕轴旋转角度为0°，椭圆弹体撞击速度由800 m/s提升至1000 m/s 时，弹体姿态角增量由18.6°降至17.8°。