椭圆变截面弹体斜贯穿薄靶姿态偏转机理

田泽， 王浩， 武海军， 邓希旻， 皮爱国， 李金柱， 黄风雷

(1.北京理工大学 爆炸与科学国家重点实验室， 北京 100081； 2.北京机电工程研究所， 北京 100074)

0 引言

近年来，异型武器平台的发展对战斗部结构设计提出了新的需求，因此非圆截面弹体对目标的侵彻与贯穿作用机理引起国内外学者的广泛关注。与传统圆截面回转体外形不同，椭圆截面弹体不但能满足导弹气动外形需求而且可以提高导弹舱室空间利用率和弹体装填比，进而提高武器终点毁伤威力与效能。王文杰等、刘子豪等、Dong等、Dai等开展了椭圆截面弹体正侵彻半无限混凝土靶实验、理论及数值模拟研究，发现了椭圆截面弹具有良好的侵彻性能和弹道稳定性，建立了椭圆截面弹体侵彻受力模型，并利用空腔膨胀理论推导了侵深公式。以上学者对椭圆截面弹体正侵彻混凝土靶开展了相关研究并取得了一定成果，对后续开展变截面椭圆弹体斜贯穿薄靶贯穿机理与姿态偏转理论分析有一定的指导与借鉴意义。

20世纪，军事装备的发展需求极大地推动了穿甲动力学的发展，Backman等、Zukas、Anderson等、Corbett等、Goldsmith、钱伟长对穿甲力学领域的研究进展进行了总结与概述。由于穿甲工况中存在目标结构多样性、靶板运动、振动或气动扰动等多种因素，弹体着靶普遍存在攻角或倾角。Goldsmith对早期非理想条件下弹靶撞击的实验研究、理论分析和数值计算等工作进行了总结，提出可以从弹体剩余速度、靶板破坏模式与弹体偏转等方面开展弹体斜贯穿薄靶的研究。Zener提出等效厚度法，即增加靶板有效厚度，将斜侵彻过程等效为正侵彻过程。此后，Awerbuch等开展了0.22 in子弹斜侵彻不同厚度的薄铝靶实验研究，采用厚度等效方法，将正穿甲理论应用到斜穿甲过程中，预测弹丸剩余速度。Zaid等忽略了弹体偏转影响，研究了不同倾角范围内截锥形弹丸斜侵彻薄靶过程，建立了剩余速度计算公式。Børvik等采用实验和数值模拟相结合的方法开展弹体斜贯穿靶板机理研究，获得了子弹剩余速度与倾角的关系。Goldsmith等、Gupta等、黄涛等、徐双喜等开展斜侵彻薄靶实验，对斜侵彻条件下靶板破坏模式进行了系统研究。Recht等根据动量和能量守恒原理得到了剩余速度公式，并提出了弹体偏转角度的半理论解析方法，得到了弹体角度偏转量的表达式，并将结论从钝头弹推广到尖头弹。Li等开展了翻转弹丸侵彻薄靶和中厚靶实验，将贯穿过程分为初始接触、初始侵入、韧性扩孔、单侧花瓣翻转4个阶段，得到了弹体剩余速度与偏转角度的唯象模型。Chen等研究了不同头部形状的刚性弹丸对厚金属板的斜贯穿，并指出厚板的贯穿过程主要由冲击函数、弹丸几何函数、靶体的无量纲厚度和冲击倾角等无量纲数决定。Deng等开展了高强度平头弹不同攻角下贯穿2A12铝合金靶数值模拟研究，对靶板失效模式、裂纹扩展，弹体体态偏转进行了研究，并指出弹体初始倾角与弹体着靶速度是影响弹体偏转的主要因素。Iqbal等开展了7.62 mm子弹斜撞击单层、多层、间隔靶数值模拟研究，结果表明倾角的存在使弹丸在贯穿多层靶时发生明显的弹道偏转。杜华池等开展了卵形弹体不同入射角侵彻多层间隔钢靶实验，并利用数值仿真方法研究了弹体入射角、弹体速度、靶体厚度及弹体变形对多层钢靶侵彻弹道特性的影响规律。

综上所述，学者们对常规圆截面弹体斜贯穿靶板从弹体剩余速度、靶板破坏模式与弹体偏转等方面，采用实验及数值模拟方法进行了研究并取得了一定成果。但是关于椭圆变截面弹体斜贯穿薄板的研究相对较少，现有文献缺乏对其作用过程和物理机制的充分探究。与常规圆截面弹体不同，椭圆变截面弹体结构上的非对称性使其在斜撞击靶板时，弹体的姿态、弹道偏转及靶板非对称破坏等现象将更加突出。由此可知，亟需根据弹体贯穿过程、靶板破坏情况对弹体受力的影响，建立椭圆变截面弹体斜贯穿薄靶板剩余速度及姿态偏转理论分析模型，讨论弹体结构对靶板破坏特征和弹体偏转的影响规律，揭示该异型弹体斜贯穿偏转运动机理。

本文在3种不同截面(圆形、椭圆形、渐变椭圆形)截头弹30°倾角斜贯穿双层间隔靶实验基础上，对椭圆截面弹体斜贯穿薄靶物理过程进行分析，依据弹体贯穿过程、靶板破坏失效模式，利用能量守恒、虚功原理等力学原理分阶段建立弹体运动学方程，获得弹道偏转模型，讨论弹体撞击速度、初始倾角、质心位置及弹体翻滚角等参数对弹体姿态偏转的影响。

1 椭圆变截面弹体斜贯穿薄靶物理过程分析

1.1 参考实验工况

王浩等开展了3种不同横截面形状的截头弹以30°倾角斜贯穿双层间隔薄钢板实验，3种弹体横截面形状分别为圆形(C型)、椭圆形(E型)和变截面椭圆形(TE型)，如图1所示。C型弹的直径为52 mm；E型弹的横截面长轴为69.7 mm，短轴为38.5 mm，长轴与短轴之比为1.8；TE型弹的弹身锥角为2.2°～4°，由C型弹经过如下变换得到：弹身锥角增加为3°，某径向坐标值和其法向坐标值分别乘以0.74和1.34。由于TE型弹体为非对称结构，为准确表征弹体着靶姿态，引入欧拉角中的翻滚角，定义弹轴与弹体横截面长轴组成的平面为弹体长轴剖面，弹体长轴剖面与水平面的夹角记为。本次实验共有4发弹体，弹长均为182 mm，弹重2.28 kg±0.03 kg，弹体撞击速度控制在260～280 m/s，实验弹体编号分别为C1、E1、TE1和TE2，其中TE1弹体与TE2弹体完全相同，E1与TE1弹体着靶姿态=0°，TE2弹体着靶姿态=90°。实验中两层靶板平行，靶板迎弹面法向与水平面夹角为30°，间距为360 mm，所用材料为舰船用945钢板。实验弹靶几何、材料参数以及实验中发射与测试技术详见文献[38]。

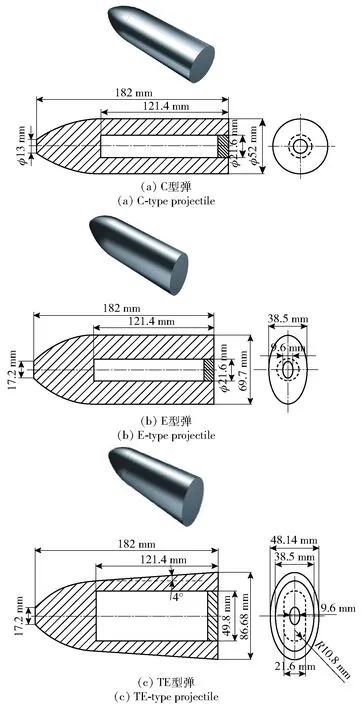
图1 弹体模型与几何结构(上为模型图，下为剖面几何结构图)Fig.1 Projectile model and geometry (upper: model diagram, lower: section geometry structure diagram)

1.2 符号约定与说明

为便于实验结果的分析与本文理论模型的建立，对实验中符号做如下约定与说明：为弹体质心，′为弹轴方向，弹体撞击速度为，贯穿第1层靶板后的剩余速度为，贯穿第2层靶板后的剩余速度为。忽略弹体绕质心的转动，以顺时针方向为正，将弹体速度在空间内分解。图2给出了弹体运动法平面和水平面内弹体攻角、倾角、姿态角的示意图。攻角为弹体速度方向与弹体轴线的夹角，倾角为弹体速度方向与靶板法向的夹角，姿态角为弹体轴线与靶板法向的夹角。由图2中的几何关系可知，=-||。

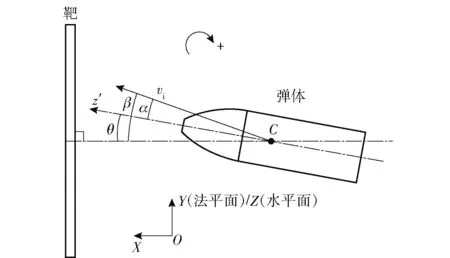
图2 弹体攻角α，倾角β，姿态角θFig.2 Yaw angle α，oblique angle β，and attitude angle θof the projectile

同时，为方便对弹体着靶后靶板破坏情况进行描述，将靶板进行分区，分别为近靶面区和远靶面区，如图3所示。

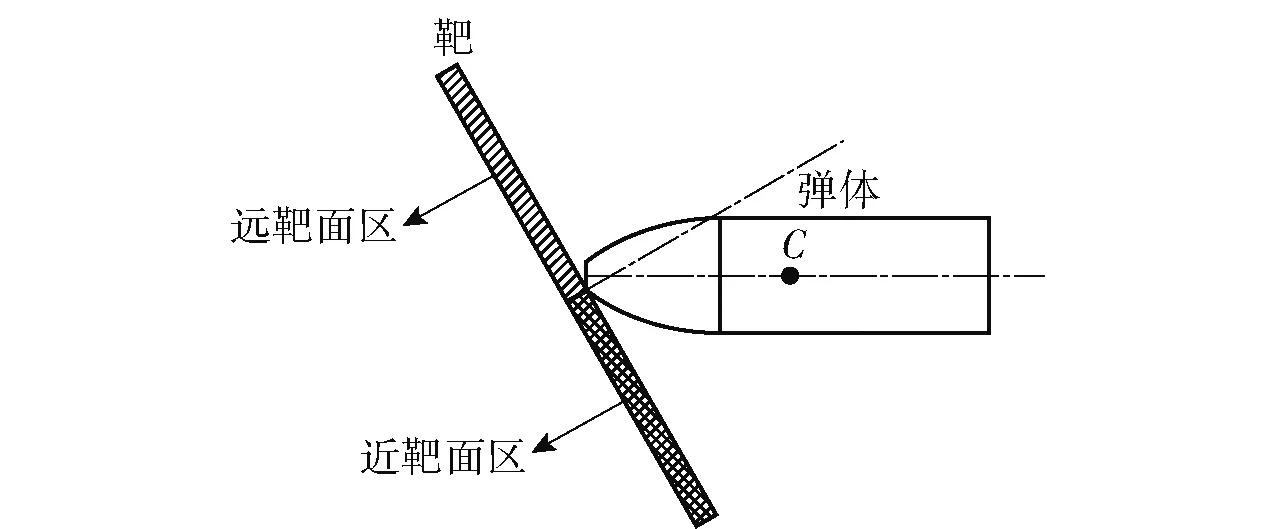
图3 靶板分区示意图Fig.3 Schematic diagram of the partitions of the target plate

1.3 弹体斜贯穿薄靶过程与实验结果分析

实验回收到的弹体整体无塑性变形且弹体头部形状完整，未发生明显变形。通过高速摄影系统记录弹体贯穿靶板的过程，得到弹体速度与姿态变化，图4、图5给出了TE型弹体两种不同着靶姿态的穿靶过程。通过TE型弹体的穿靶过程及TE型弹体自身结构特点可知：弹体撞击靶板时，弹体截锥头部首先接触靶板形成凹坑；然后弹体头部贯穿靶板并形成与截头处形状相当的冲塞块，靶板由于弹体头部挤压、扩孔形成花瓣形破坏；最后弹身挤压并贯穿靶板；弹体以不同的着靶姿态贯穿靶板，弹体的姿态偏转具有明显区别。

图4 γpt=0°时TE型弹体穿靶过程Fig.4 The process of a TE-type projectile penetrating the target when γpt=0°

图5 γpt=90°时TE型弹体穿靶过程Fig.5 The process of a TE-type projectile penetrating the target when γpt=90°

通过回收靶板观测研究不同工况下靶板的变形与失效模式。实验中不同弹体运动数据及靶板破坏模式整理结果如表1和表2所示，其中倾角一般由2个正交分量确定，若法平面内倾角为，水平面内倾角为，则倾角=arctan(tan+tan)05。

分析表1和表2中的数据可知：实验条件下3种弹体贯穿双层间隔薄靶后，速度损失相差不大；3种弹体贯穿薄靶所形成的弹孔与自身横截面形状相似，C型弹形成近似圆形弹孔，E型弹与TE型弹形成椭圆形弹孔；3种弹体贯穿薄靶过程中均出现剪切冲塞现象，并伴随有花瓣形破坏，靶板的花瓣形破坏主要发生在靶板远靶面一侧，且花瓣的挠曲变形较大；由于结构上的非对称性，对于E型弹与TE型弹，当=0°和或=90°时，靶板表现出不同形貌的花瓣形破坏。对于TE型弹体，当=0°时，由于截头的剪切冲塞作用，靶板上形成与截头形状相似的剪切块，靶板远靶面一侧由于拉伸作用形成明显花瓣，近靶面一侧未因环向拉伸作用开裂；当=90°，靶板远靶面一侧形成一个长条形状的花瓣，在条形花瓣两侧伴随2～3个尺寸较小的花瓣，在弹体水平两侧中心位置受拉伸作用开裂，各形成1～2个花瓣。

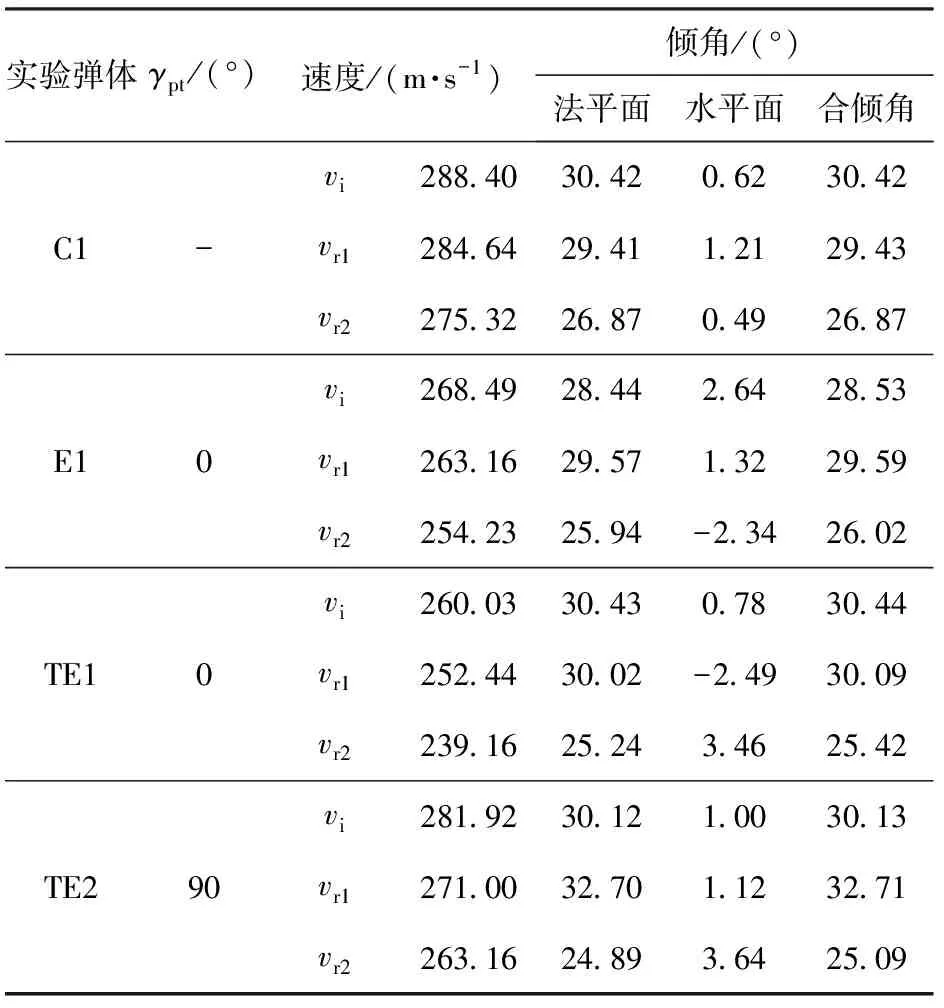
表1 斜贯穿弹体运动数据

表2 靶板变形与破坏模式

2 TE型弹体斜贯穿薄靶姿态偏转理论模型建立

依据第1节TE型弹斜贯穿双层间隔薄靶实验中穿甲过程、靶板破坏情况、弹体速度与姿态角变化等物理作用过程的分析，针对图6所示弹体几何结构，进行TE型弹体斜贯穿平板过程中弹体剩余速度及弹体姿态变化理论建模。图6中：为弹体质心；为截顶长度；为包含截顶的弹体头部长度；为弹尖到弹体质心的距离；为包含截顶弹体全长；、分别为截顶椭圆横截面的长、短半轴；、分别为弹头与弹身交接处椭圆横截面的长、短半轴；、分别为弹尾处椭圆横截面的长、短半轴。

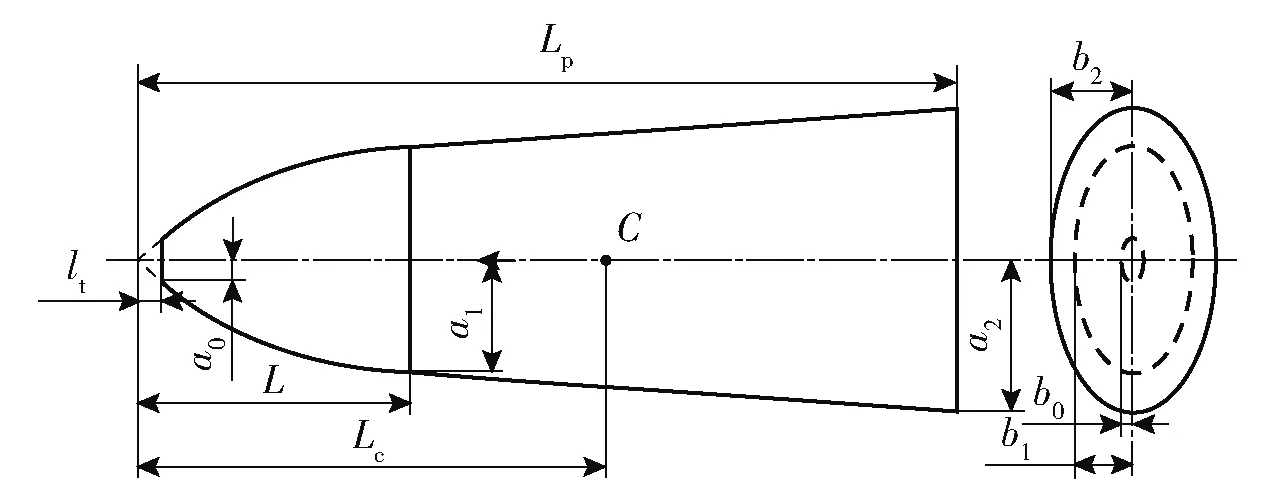
图6 TE型弹体几何模型Fig.6 Geometric model of a projectile with a variable elliptical cross-section

2.1 模型假设

为简化斜贯穿问题，便于理论模型建立，仅对=0°和=90°两种典型条件下弹体斜贯穿平板进行理论分析，并作如下假设：

1)速度方向与弹轴重合，即攻角为0°；

2)弹体为刚体，只受到弹靶接触力作用，忽略弹体重力、空气阻力、摩擦力等其他力的影响；

3)弹体的运动仅在射平面内，不考虑弹体在其他平面的及绕弹轴旋转的运动；

4)忽略弹体绕质心旋转运动引起的阻力作用。

2.2 弹体运动分析

如图7所示，为表征弹体在射平面内的运动，建立以质心为原点，沿弹轴方向和运动平面内垂直于弹轴方向，建立弹体运动坐标系。沿靶板法向和靶面垂直于法向方向，建立靶板固定坐标系。弹体质心受力和力矩及其正方向如图7所示。图7中，为弹体的轴向合阻力，为横向合阻力，为过弹体质心的转动力矩，为初始倾角。

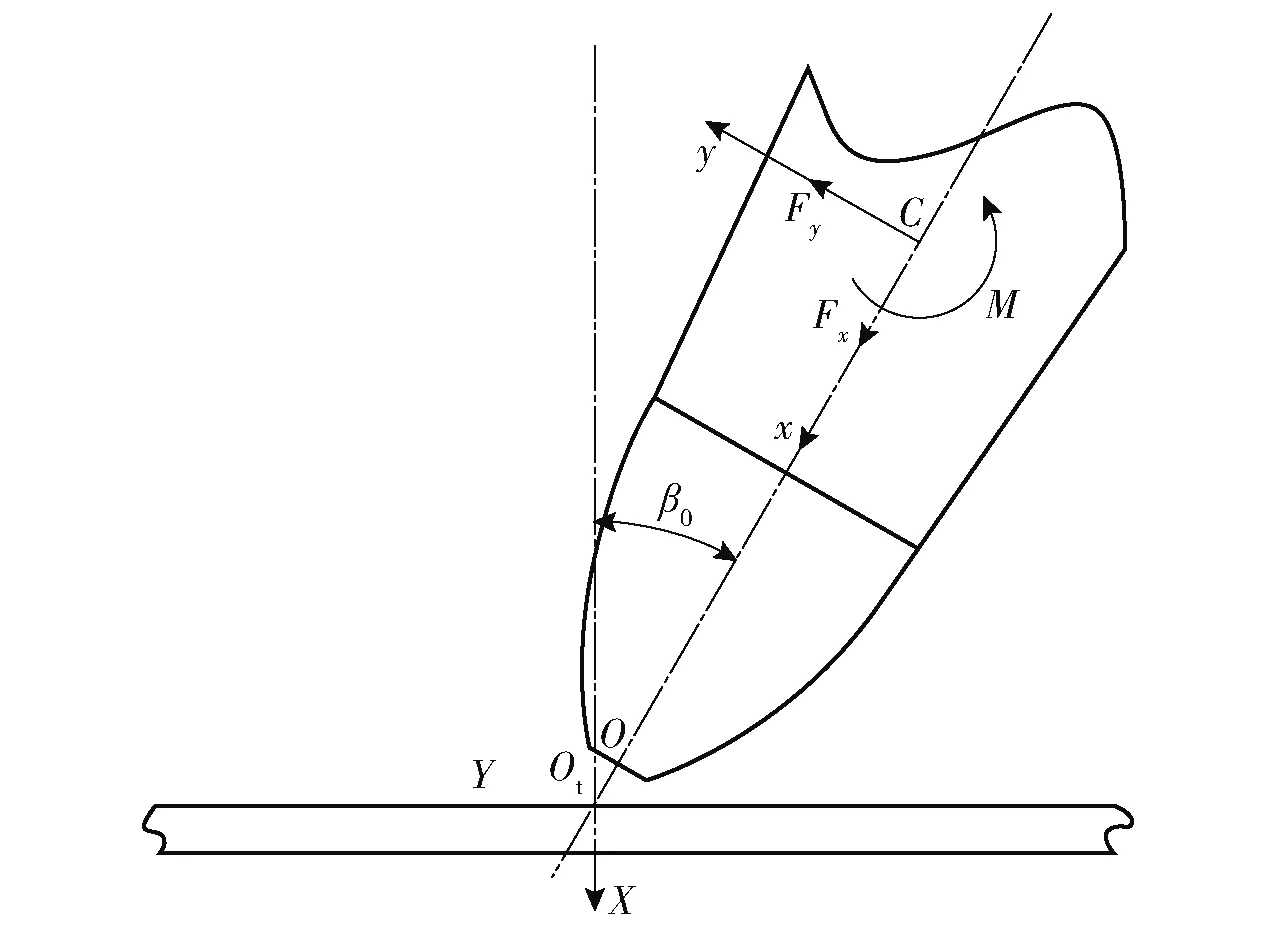
图7 坐标系与弹体受力分析Fig.7 Coordinate system and mechanic analysis of the projectile

根据运动学原理，弹体质心运动方程为

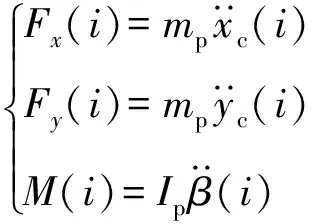
(1)

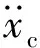
结合初始条件

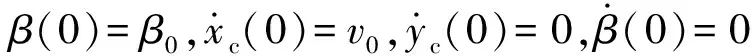
(2)

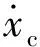
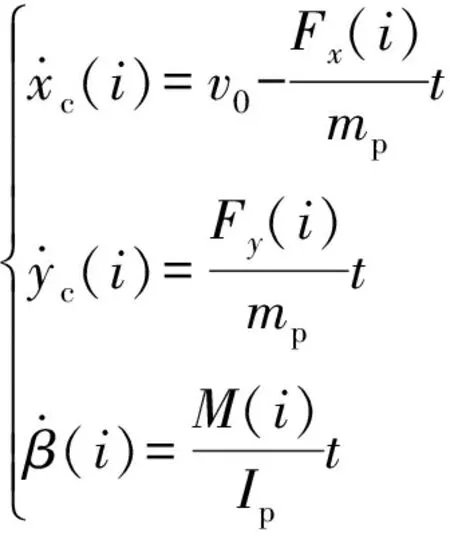
(3)

在+Δ时刻，弹体轴和轴方向的速度、角速度为

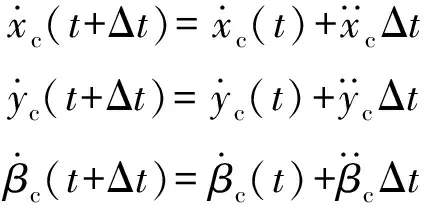
(4)

弹体运动的位移、角度为

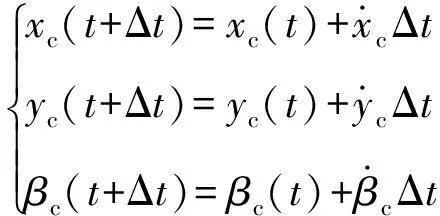
(5)

弹体速度由弹体坐标系向地面坐标系(靶板坐标系)转换得到：

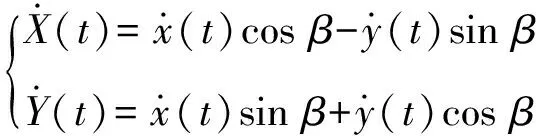
(6)

地面坐标系弹体位移为

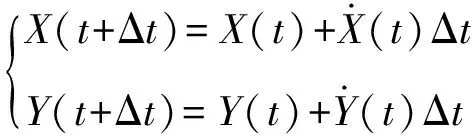
(7)

2.3 弹体斜贯穿姿态偏转分析

从22节中对弹体的运动分析可知，如果能给出弹体斜贯穿靶板过程中的受力和力矩，则根据弹体运动学方程，便可以预测弹体斜贯穿靶板过程中的速度与姿态。根据靶板破坏特征与弹靶位置关系，将斜贯穿过程依次分为弹体头部压入阶段、头部贯穿阶段、过渡阶段、弹身贯穿阶段。根据各阶段弹靶作用过程，对弹体进行受力分析。

231 第1阶段：弹体头部压入阶段(0≤≤2tan)

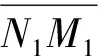
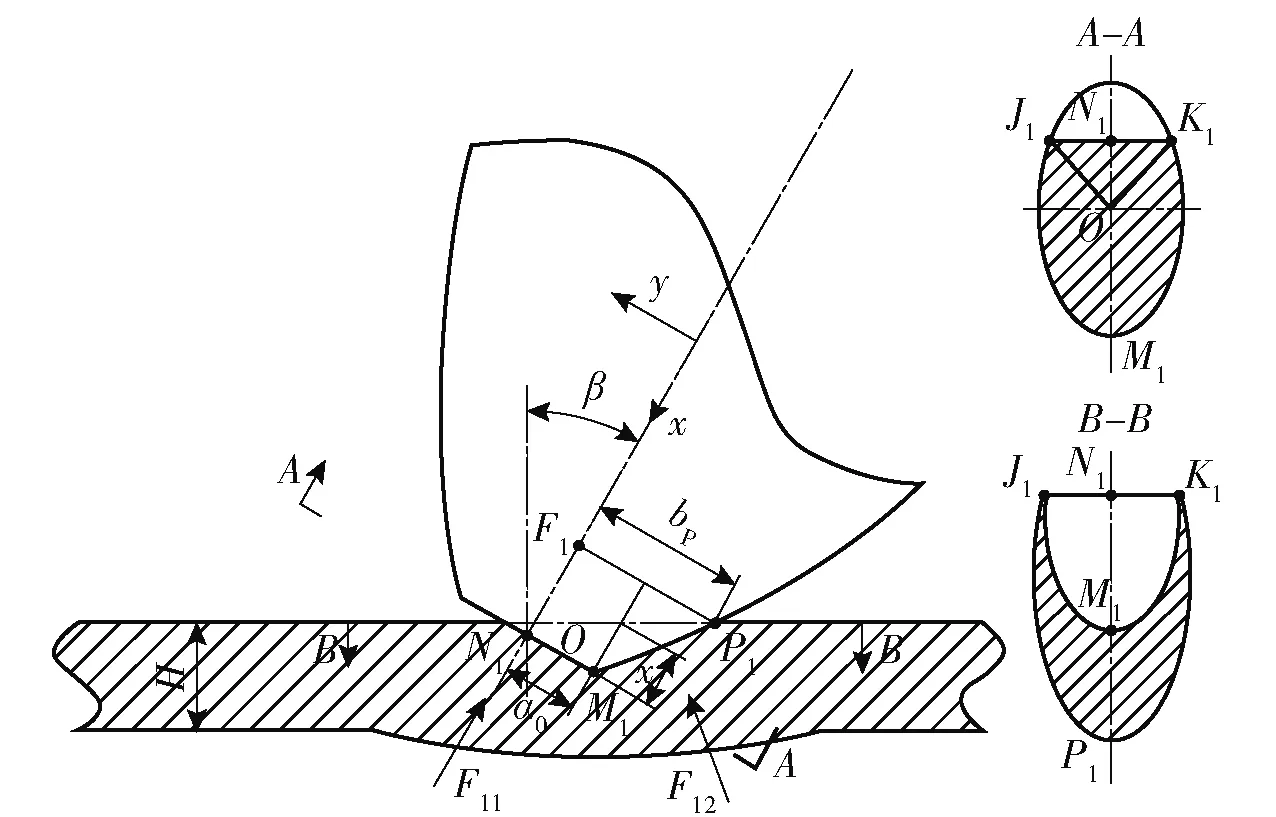
图8 弹体头部压入阶段Fig.8 Press-in of the projectile nose

如图8中截面-所示，弹体头部截锥与靶板的接触面积为

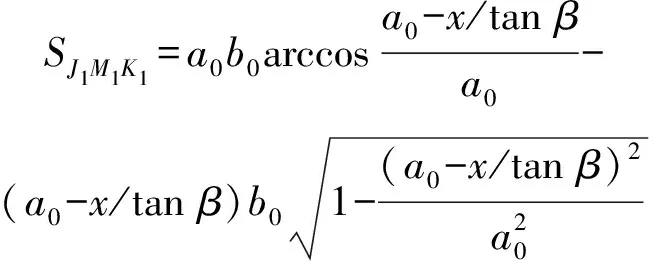
(8)

如图8中截面-所示，弹体头部侧面的接触面积为

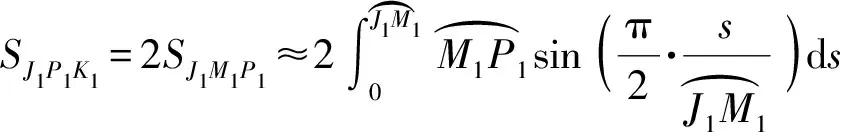
(9)

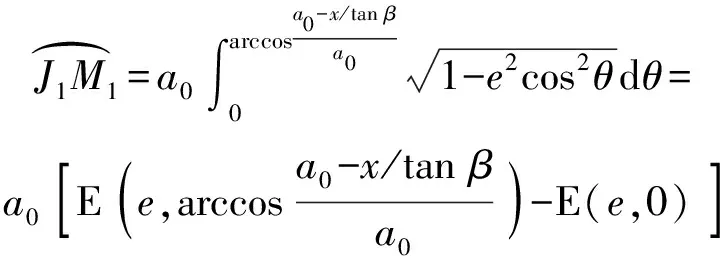
(10)

式中：为积分变量，表示弧长；为弹体头部侧面接触面积的一半；为椭圆的离心率；E(·)表示定积分的原函数。

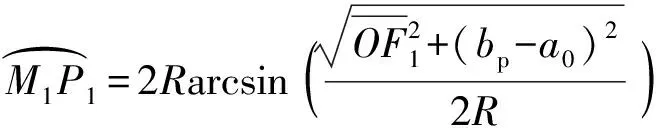
(11)

为弹体头部圆弧半径。

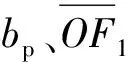
(12)

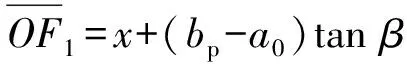
(13)

作用在弹体表面的作用力为

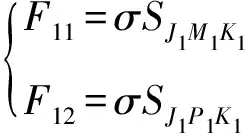
(14)

式中：为靶板的屈服强度。

作用在弹体质心的阻力和力矩为

(15)

根据求得的力与力矩，结合弹体质心运动方程(1)式与初始条件(2)式，积分得到弹体轴、轴方向的速度及角速度，进一步可求得+Δ时刻的弹体速度、角速度、位移与角度，进而通过坐标变换得到弹体对地面坐标系的速度与位移，其他阶段中弹体运动过程求解方法与第1阶段相同。

232 第2阶段：弹体头部贯穿阶段(2tan≤≤--tan+tan)

弹体头部完全压入靶板后，随着弹体继续运动，在截锥面前端形成椭圆形状的冲塞块。在弹体近靶面一侧，由于弹体头部平行于靶面的挤压作用，在弹体头部前端形成偏离弹道方向的花瓣形破坏。在弹体远靶面一侧，由于靶板扩孔变形产生的环向拉伸作用形成花瓣形破坏，如图9所示。图9中，、、为弹体与靶板接触的点，和分别为点和到弹体轴线的垂足，为弹体轴线与靶板迎弹面的交点，为过弹体截头端点平行于弹体轴线与靶板迎弹面的交点，为前花瓣对弹体的阻力，为环向花瓣弯曲变形引起弹体阻力。

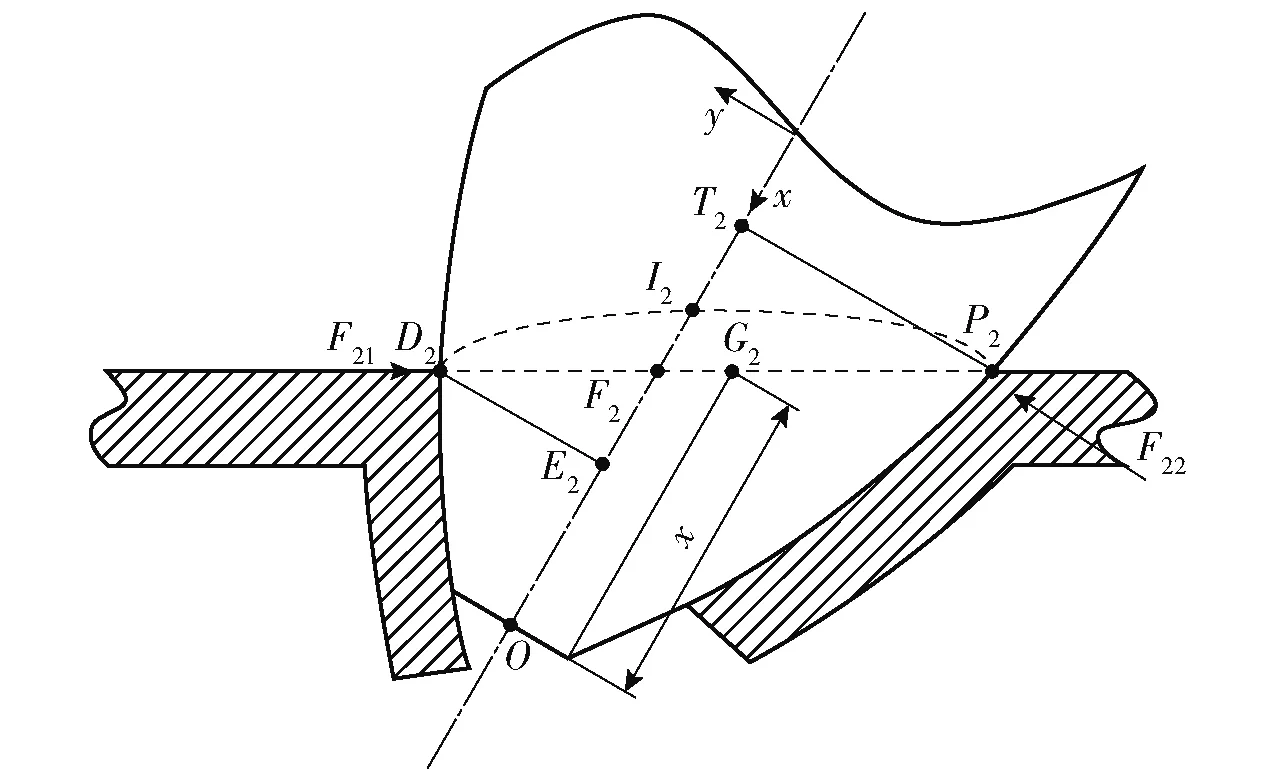
图9 弹体头部贯穿阶段Fig.9 Penetration of the projectile nose

下面分别对该阶段塞块、前花瓣、环向花瓣变形对弹体产生的阻力进行分析。

1)塞块的剪切冲塞。假设剪切冲塞阻力作用点为，方向沿轴负方向，则剪切阻力做功为

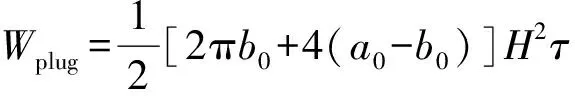
(16)

式中：为靶板的剪切强度。

塞块的动能为

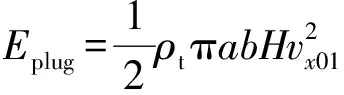
(17)

式中：为靶板的密度；01为第1阶段后弹体轴方向的速度。

根据能量守恒，得到

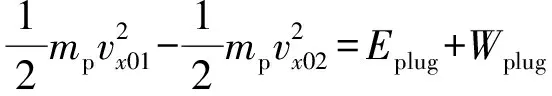
(18)

式中：02为弹体发生剪切冲塞变形后的剩余速度。

2)前花瓣剪切变形功为

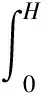
(19)

式中：为花瓣宽度；为积分变量，为靶板内微元。

3)前花瓣弯曲变形功为

=

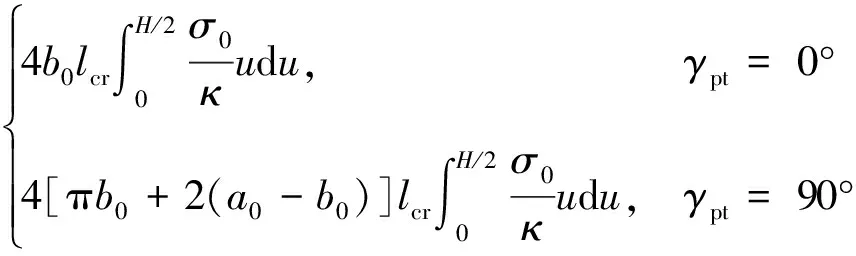
(20)

式中：为靶板材料静态屈服强度；曲率=(2)，为材料的失效应变。

4)前花瓣的动能。忽略弹体绕质心的转动速度影响，则

=(sin+cos)

(21)

式中：为前花瓣的速度。

根据虚功原理，前花瓣对弹体的阻力为

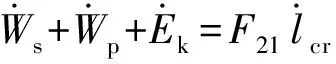
(22)

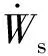
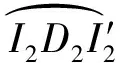
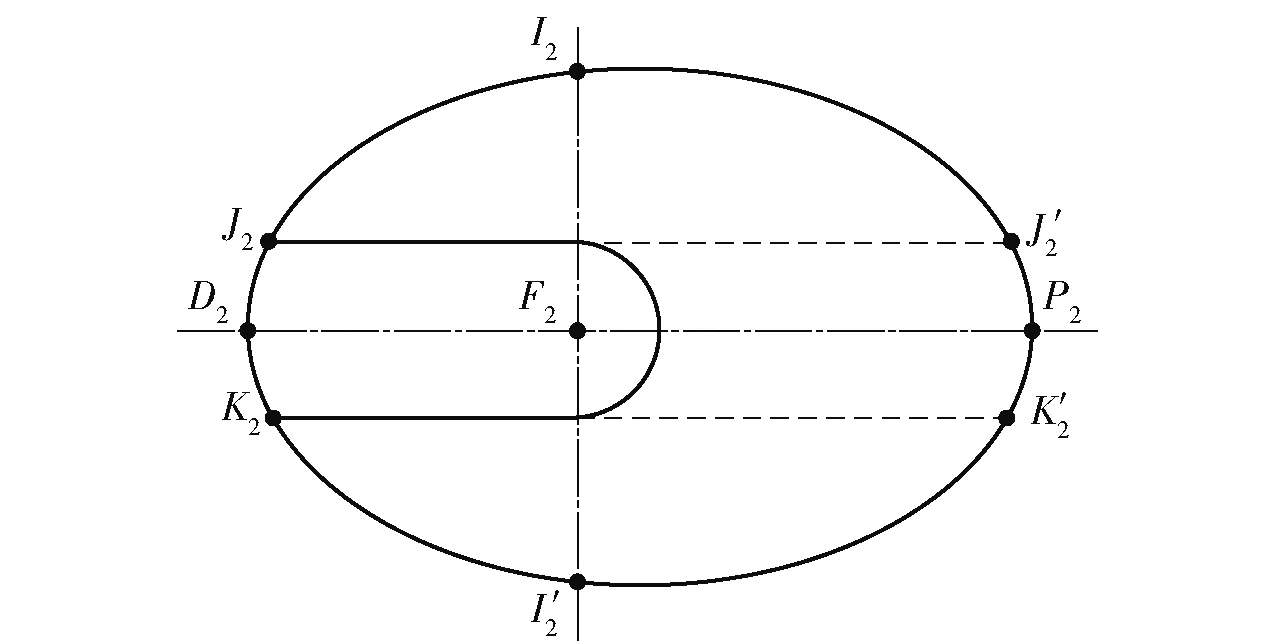
图10 花瓣弯曲变形俯视图Fig.10 Top view of the petal bending deformation

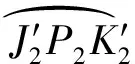
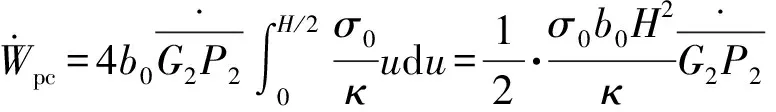
(23)

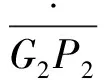
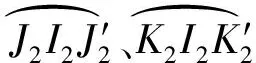
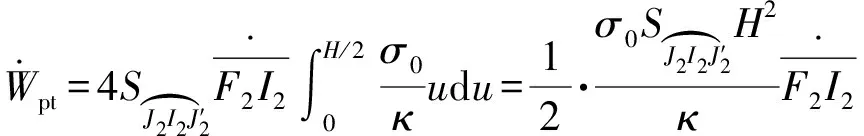
(24)

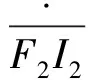
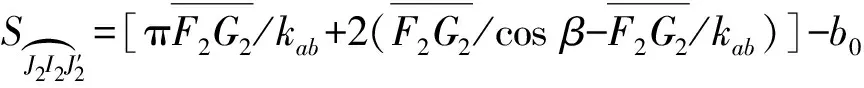
(25)

为长短轴之比，

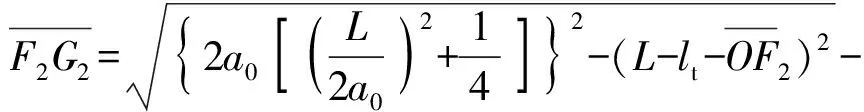
(26)

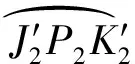
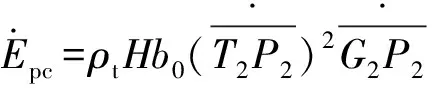
(27)

式中：

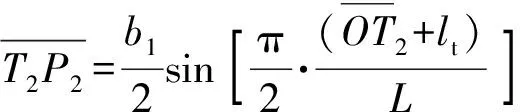
(28)

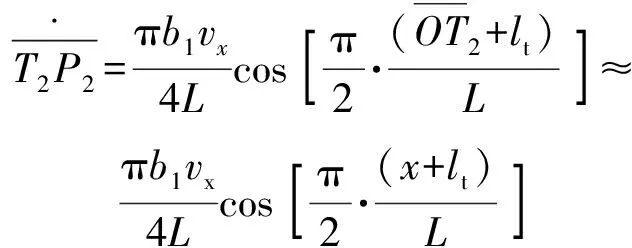
(29)

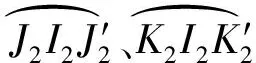
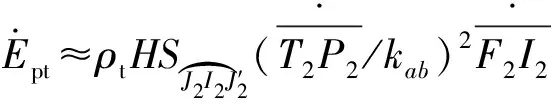
(30)

根据虚功原理，得

(31)

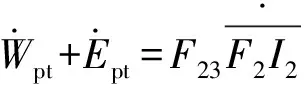
(32)

式中：和为环向花瓣弯曲变形引起的弹体阻力。

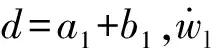
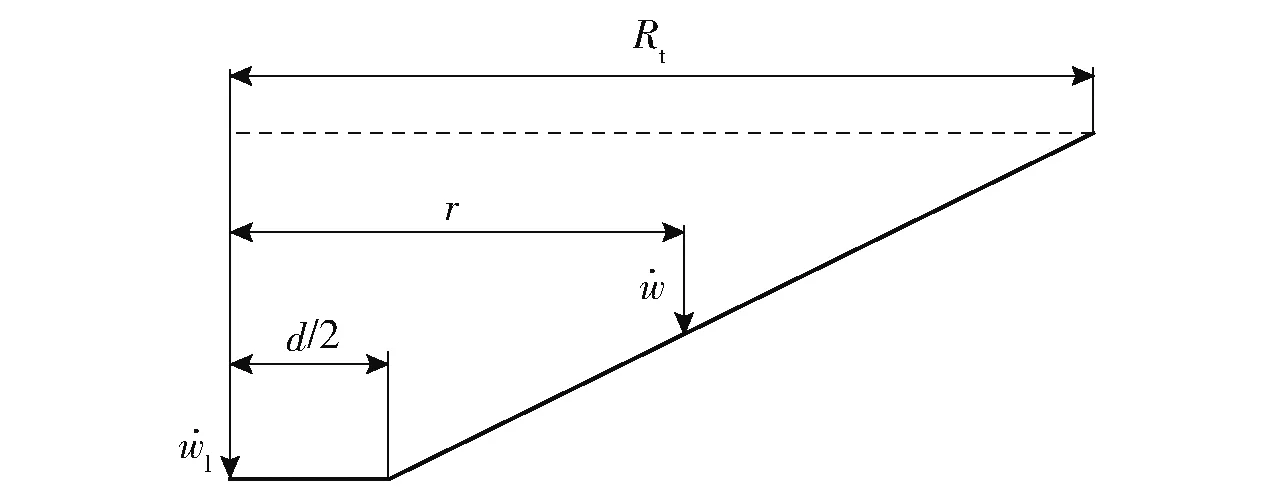
图11 靶板结构变形速度场Fig.11 Velocity field of the target plate’s structural deformation

速度场表达式为

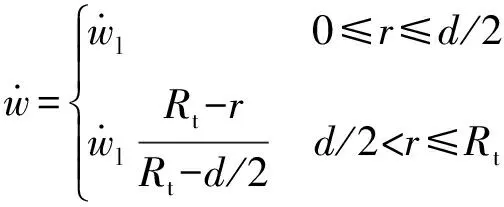
(33)

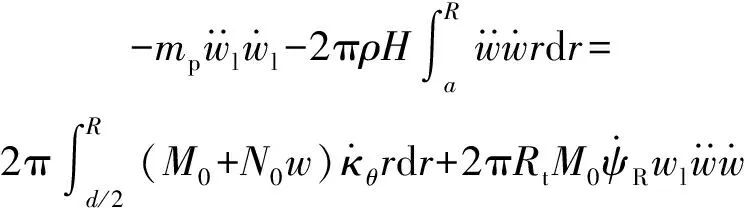
(34)

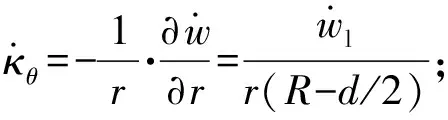
使用Cowper-Symonds模型考虑应变率效应，

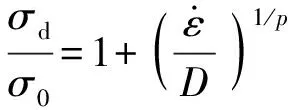
(35)

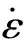
由能量守恒定律得

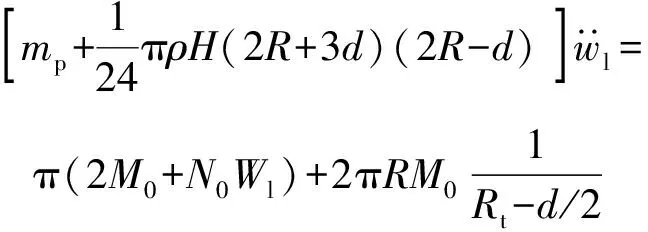
(36)

由牛顿第二定律，得

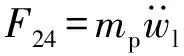
(37)

式中：为靶板变形引起的弹体轴向阻力。

此阶段弹体受到的力与力矩为

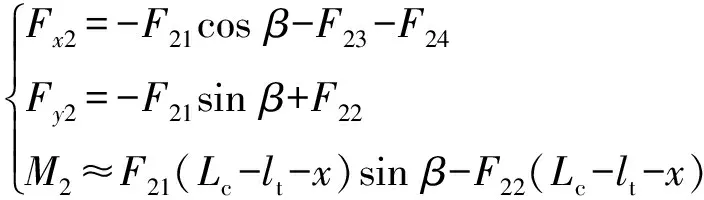
(38)

233 第3阶段：过渡阶段(--tan+tan≤≤-+(+)tan)

该阶段为弹体头部与弹身连接处依次穿过靶板的近靶面一侧和远靶面一侧，在此过程中环向花瓣弯曲变形和转动由弹体近靶面一侧开始向另一端逐渐消失，如图12所示。由于该阶段在弹体整个贯穿过程中历时较短，忽略环向花瓣弯曲和转动对弹体运动的影响。前花瓣剪切、弯曲、动能变形功计算与第2阶段相同。图12中，和为弹体与靶板接触的点，和分别为点和到弹体轴线的垂足，为弹体轴线与靶板迎弹面的交点，为弹体头部与弹身交界面与弹体轴线的交点，为过弹体截头端点平行于弹体轴线与靶板迎弹面的交点，为弹头与弹身交界面端点到靶板迎弹面的垂足，为前花瓣对弹体的阻力，为花瓣变形引起弹体阻力。

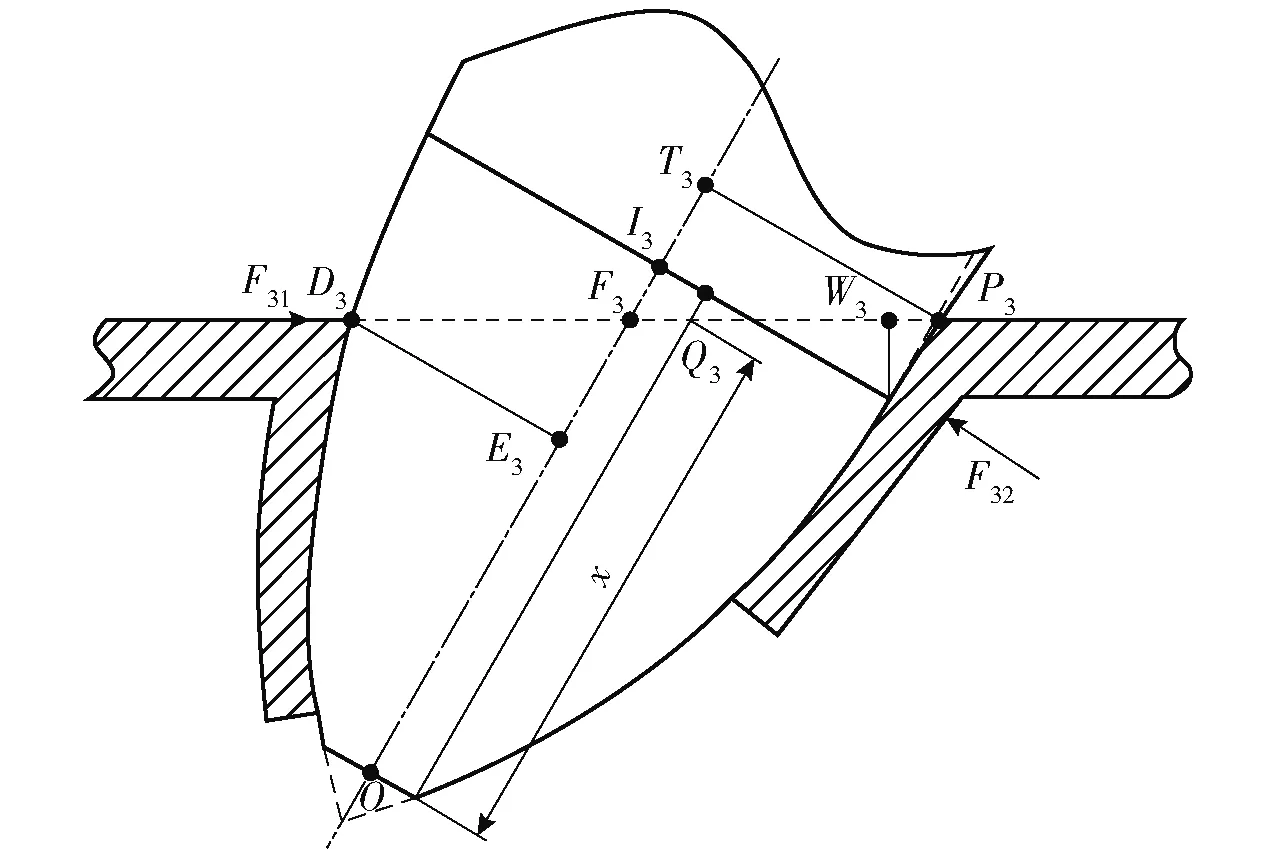
图12 过渡阶段Fig.12 Transitional stage

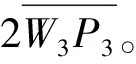
花瓣剪切变形功

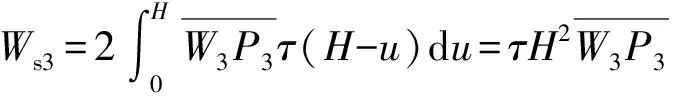
(39)

由虚功原理得

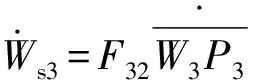
(40)

弹体受到的力与力矩为

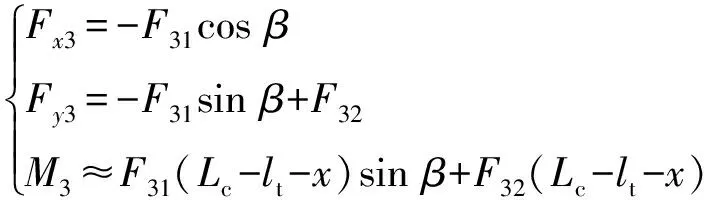
(41)

234 第4阶段：弹身贯穿阶段(-+(+)·tan≤≤-)

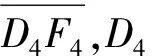
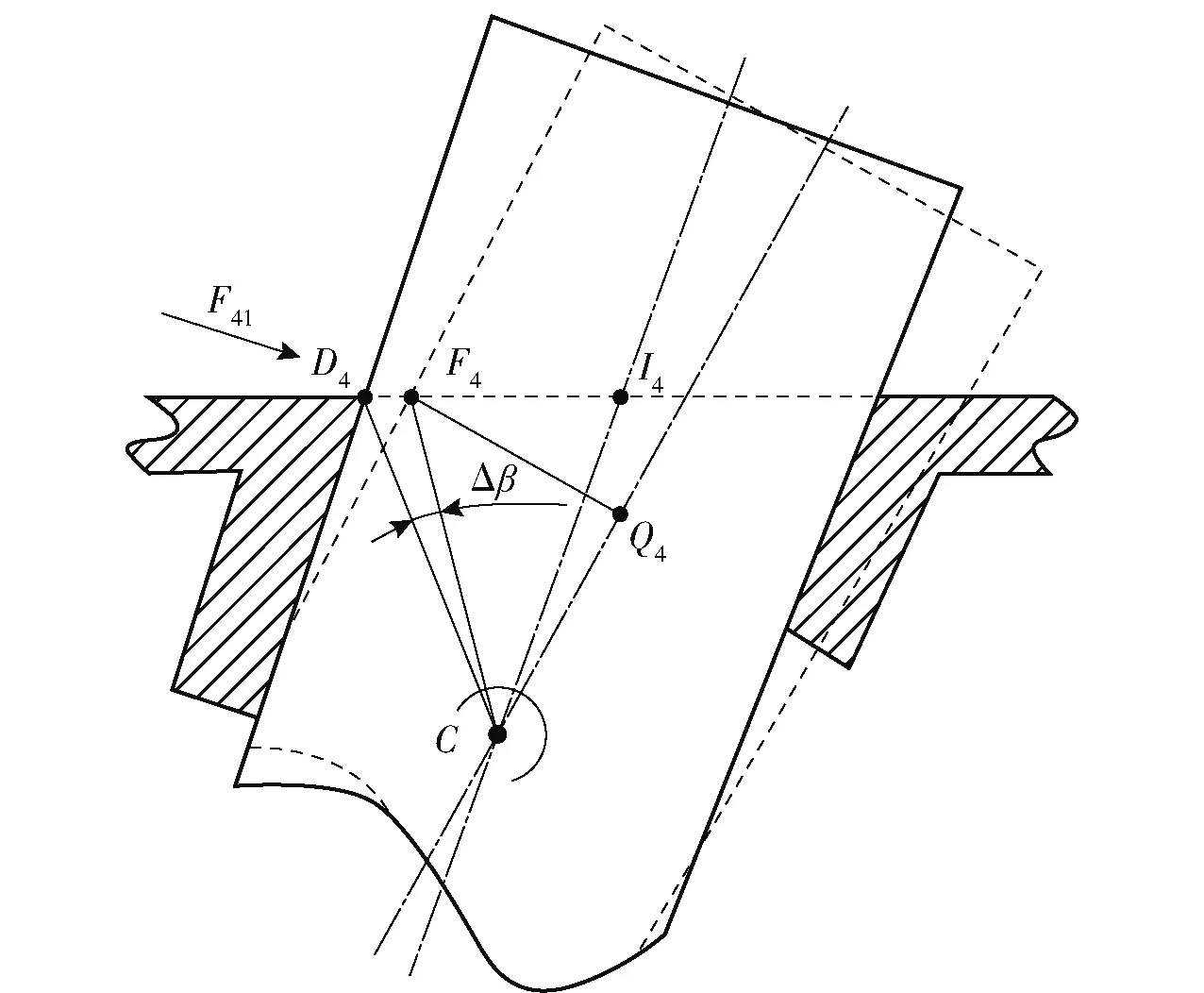
图13 弹身贯穿阶段Fig.13 Penetration of the projectile body

花瓣剪切变形率为

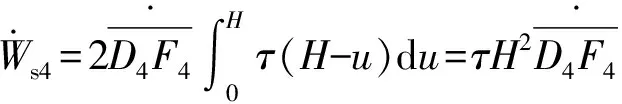
(42)

花瓣弯曲变形率

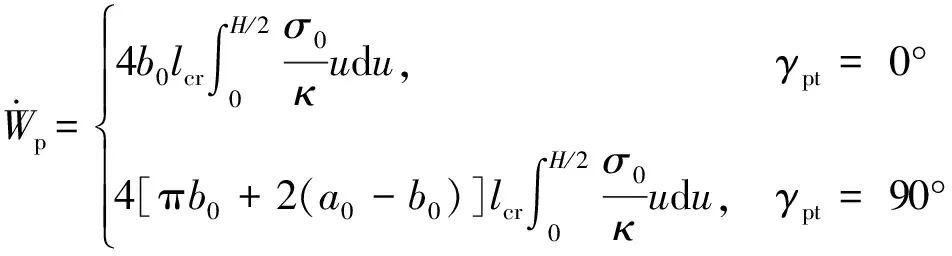
(43)

由虚功原理，得

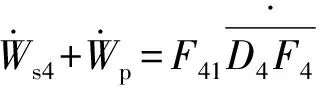
(44)

弹体受到的力与力矩为

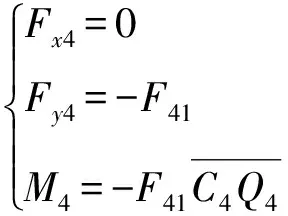
(45)

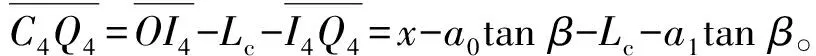
3 模型验证与参数影响分析

3.1 模型验证

用本文提出的椭圆变截面弹体斜贯穿姿态偏转理论模型，计算实验条件下弹体贯穿第1层靶版的剩余速度与姿态偏转角，弹靶几何参数及材料参数均与文献[38]相同。本文计算模型采用MATLAB软件进行编程计算，4次实验中弹体计算所用主要几何参数在表3中给出。

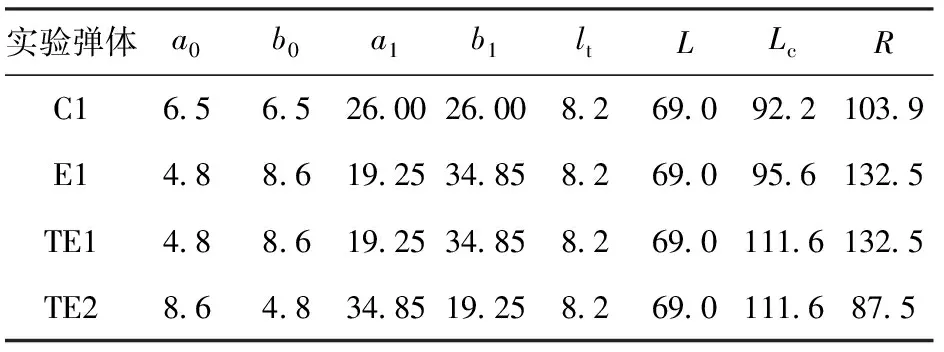
表3 实验弹体主要几何参数

利用分步迭代法得到弹体穿靶过程中的速度和偏转角度的时程曲线，如图14所示。由图14可知：4组实验中，弹体轴方向速度大小与弹体法平面内合速度大小的改变主要发生在弹体贯穿薄靶板的前3个阶段，在弹身穿透靶板的过程中几乎不变；弹体轴方向的速度大小与弹体姿态偏转角度的变化则在第3和第4个阶段更为明显；初始撞击速度越大，速度降越小；TE型弹体以不同的翻滚角=0°和=90°撞击靶板时，偏转角度明显不同。这些结论符合弹体侵彻薄靶的基本规律，并且与实验中观测到的现象相符。

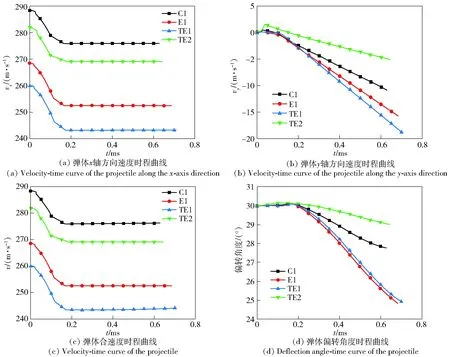
图14 计算模型所得弹体速度及偏转角度随时间的变化Fig.14 The velocity and deflection angle of the projectile change with time obtained by the calculation model

表4给出了斜贯穿实验与理论模型计算结果。由表4可见，由于弹体姿态偏转角度数值上比较小，表中使用绝对误差表征本文理论模型计算可靠性。由表4中实验结果与理论模型预测值对比可知，弹体以30°倾角贯穿薄靶后，弹体剩余速度相对误差不超过3%，弹体姿态偏转角绝对误差小于7°，该理论模型在实验工况下的可靠性得到验证。

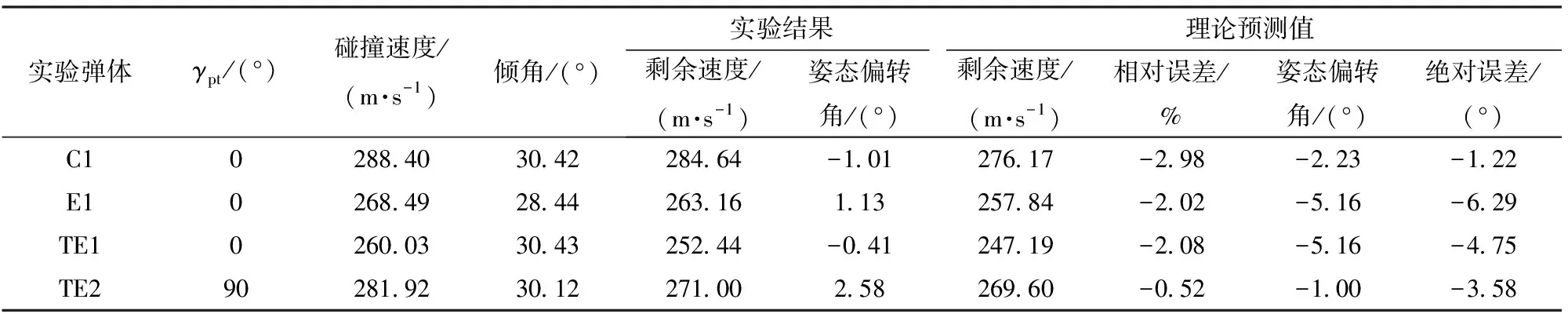
表4 文献[38]斜贯穿实验结果与本文理论模型计算结果对比

为进一步验证理论模型的可靠性，提取文献[38]椭圆变截面弹体不同倾角、不同撞击速度及不同姿态条件下数值模拟中弹体贯穿第1层靶板的姿态偏转与本文理论模型计算结果进行对比，如表5所示。对比表5中的数据发现：本文理论模型在45°倾角条件下，弹体贯穿靶板后的剩余速度与弹体姿态偏转吻合良好，弹体剩余速度相对误差不超过6%，弹体姿态偏转角绝对误差小于2°；当弹体初始倾角大于60°时，结果出现较大偏差，表明本文理论模型将不再适用。

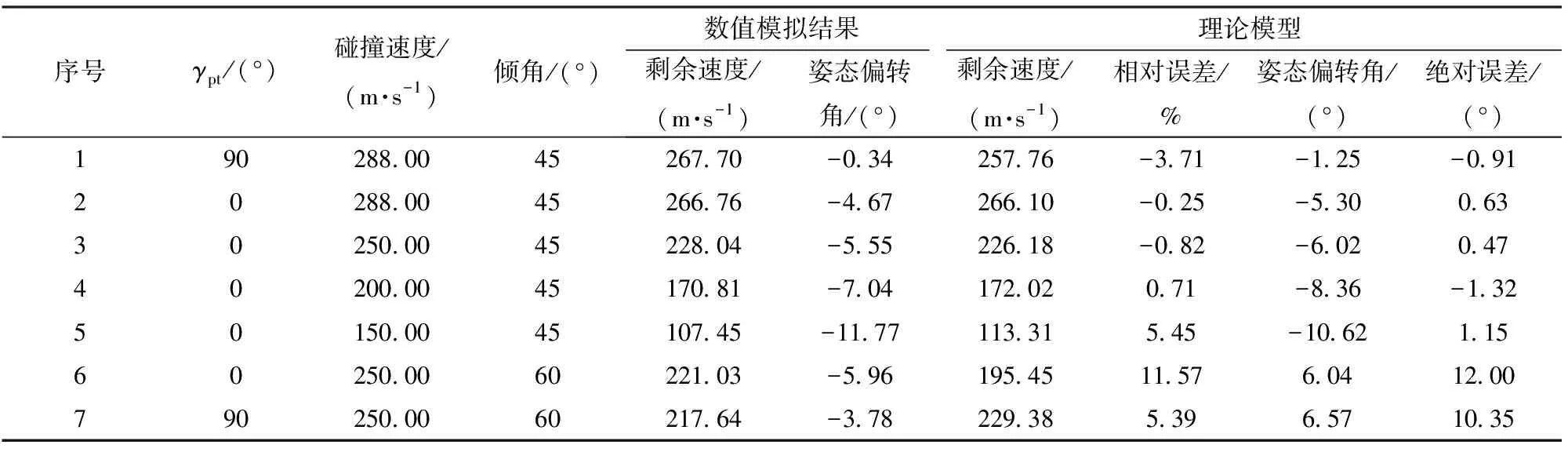
表5 文献[38]TE型弹体斜贯穿数值模拟结果与本文理论模型计算结果对比

3.2 参数影响分析

通过文献[38]中实验与数值仿真结果对本文椭圆变截面弹体斜贯穿薄靶姿态偏转理论可靠性的验证，证明本文提出的理论模型可以准确描述椭圆变截面弹体斜侵彻薄靶过程，可用于弹体姿态偏转规律研究。相关研究表明，影响圆截面弹体姿态偏转的因素主要有撞击速度、弹体初始角、弹体侵蚀变形、弹体形状等。由于本文所研究撞击速度较低，弹体未发生侵蚀与变形，弹体近似认为是刚性的，不考虑弹体侵蚀变形。为进一步研究椭圆变截面弹体贯穿薄靶的影响因素，下面将开展弹体撞击速度、初始倾角、质心位置、弹体姿态(=0°或=90°)及弹体长短轴之比对弹体姿态偏转影响规律的参数分析。

3.2.1 撞击速度对弹体姿态偏转的影响

利用本文理论模型，对不同撞击速度条件下TE型弹体姿态偏转进行计算，弹靶几何、材料参数与文献[38]相同，弹体翻滚角=0°，弹体初始倾角=30°，理论模型计算结果如图15所示。由图15可见：随着弹体撞击速度的增加，弹体姿态偏转角度呈现指数型减小趋势；与低速条件相比，高速条件下的弹体姿态偏转较小，主要是弹体贯穿靶板的时间减少，偏转力矩对弹体的累积作用减弱造成的。

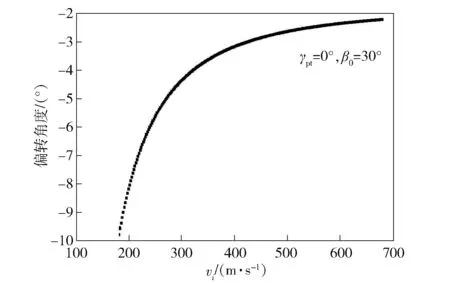
图15 弹体姿态偏转角度随碰撞速度的变化Fig.15 Correlation between the attitude deflection and the impact velocity

3.2.2 初始倾角对弹体姿态偏转的影响

保持撞击速度为288 m/s，弹体翻滚角=0°，利用本文的理论模型对不同初始倾角条件下体姿态偏转角度进行计算。理论模型计算结果如图16所示。图16的结果表明：弹体姿态偏转量随着弹体初始倾角的增大而增大；随着初始倾角的增大，弹体与靶板接触面积变大，弹体的侧向作用力增大，导致弹体质心处偏转力矩增大，弹体姿态偏转角度也随之增大。

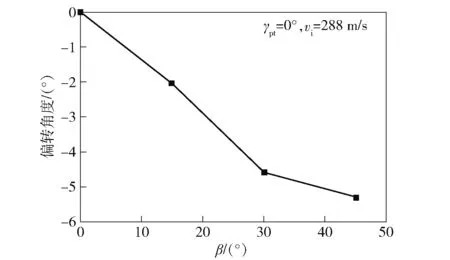
图16 弹体姿态偏转角度随初始倾角的变化Fig.16 Correlation between the attitude deflection and the initial oblique angle

3.2.3 质心位置对弹体姿态偏转的影响

保持TE型弹体几何形状不变，撞击速度288 m/s，弹体翻滚角=0°，初始倾角=30°，仅改变质心位置，利用本文理论模型计算弹体偏转角度，结果如图17所示。从图17中可以发现，随着弹体质心位置偏离弹尖越远，弹体姿态偏转越大。表明在弹体结构设计中弹体质心越靠前、姿态越稳定。分析原因，弹体的偏转主要发生在前3个阶段，质心位置距离弹头越近，靶板对弹体质心的偏转力矩越小，弹体在贯穿靶板过程中偏转越小。

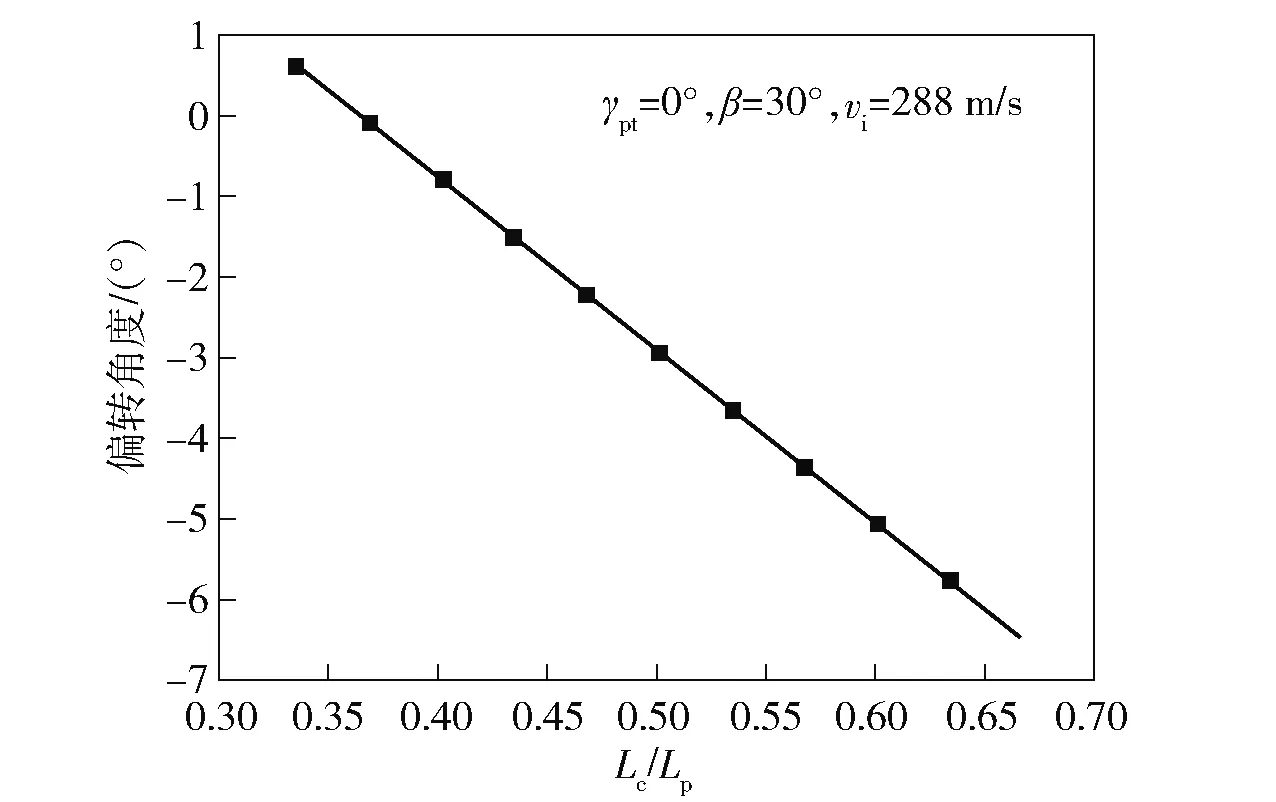
图17 弹体姿态偏转角度随质心位置的变化Fig.17 Correlation between the attitude deflection and the centroid position

3.2.4 弹体翻滚角对弹体姿态偏转的影响

由于TE型弹体的非对称结构特性，弹体以不同的翻滚角=0°和=90°斜撞击靶板时，靶板破坏模式及弹体受力情况不同，导致弹体姿态偏转规律明显不同。结合图15，仅改变弹体姿态，令=90°，探究弹体初始姿态对弹体姿态偏转角的影响。如图18所示，当=90°时，相同初始条件下弹体姿态偏转角较小。根据理论模型中弹体侧向力与弹体与靶板的接触面积正相关，当=90°弹体横截面长轴一侧与靶板接触面积小于=0°时弹体短轴与靶板的接触面积，因此弹体受到的侧向力较小，从而靶板对质心的偏转力矩较小，导致当=90°时弹体的偏转较小。

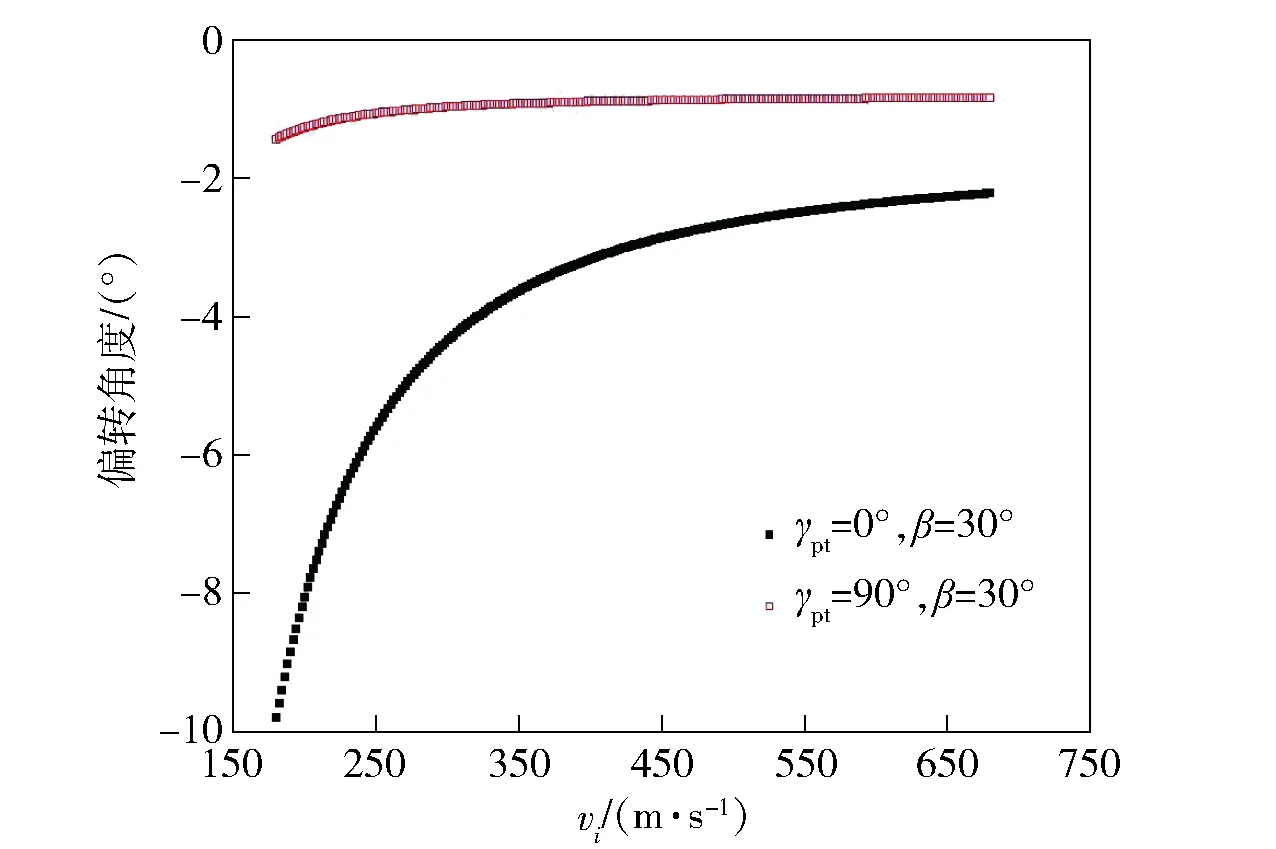
图18 弹体不同姿态贯穿薄靶偏转角度对比Fig.18 Correlation between the attitude deflection angle and the projectile attitude after penetration

3.2.5 长短轴之比对弹体姿态偏转的影响

椭圆截面长短轴之比也是椭圆变截面弹结构非对称性的一个显著特点，因此开展不同长短轴之比TE型弹体姿态偏转规律的研究。为实现单一变量分析，采用控制变量法，弹体质量与体积保持不变，仅改变椭圆弹体横截面长短轴的比值。如图19所示，TE型弹体撞击速度288 m/s、初始倾角30°、不同长短轴之比下两种翻滚角条件下弹体的姿态偏转结果。图19结果表明：当=0°时，随着长短轴之比增大，弹体姿态偏转角度随之增大；当=90°时，随着长短轴之比的增大，弹体姿态偏转角随之减小。弹体在两种翻滚角条件下，长短轴之比的变化导致相反的姿态角变化规律，主要原因在于弹体以不同姿态撞击靶板侧向力不同。

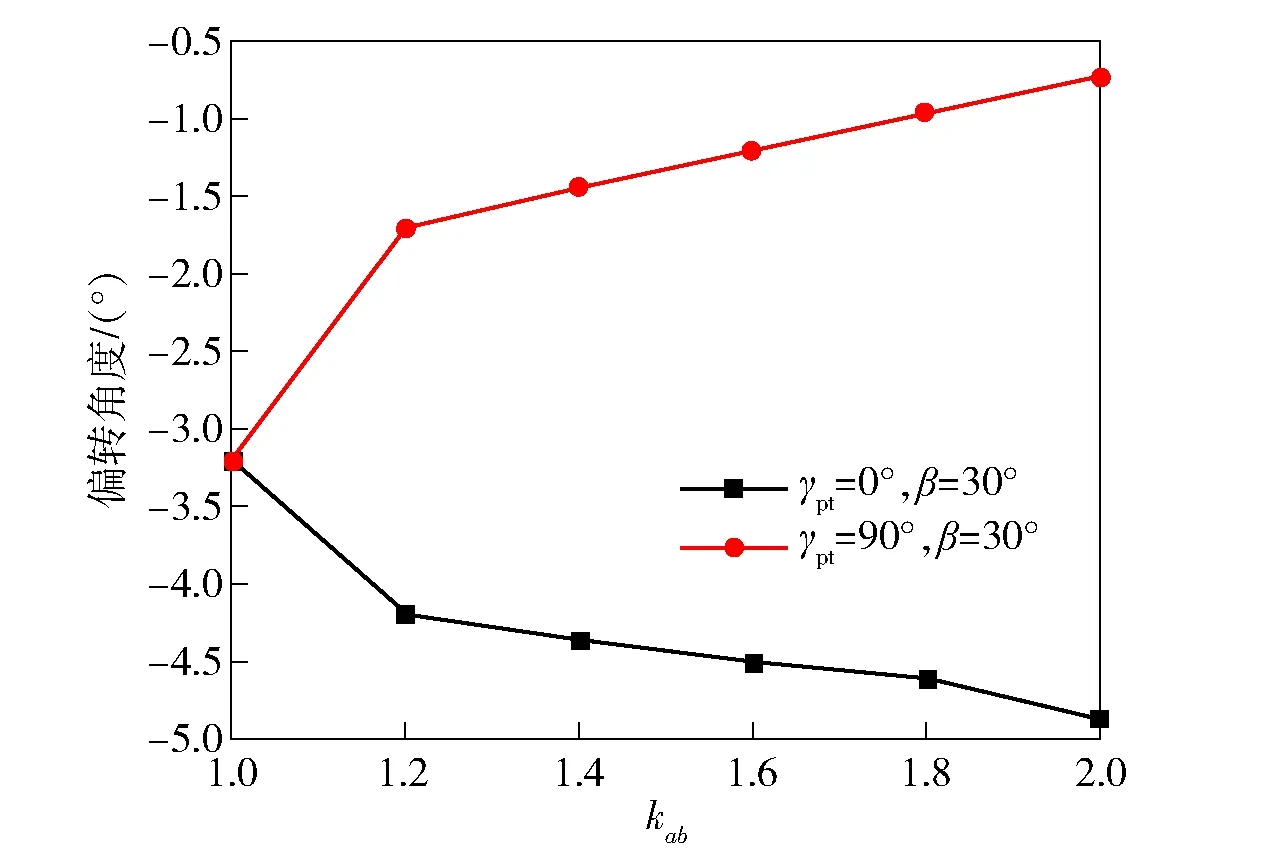
图19 长短轴之比对弹体姿态偏转的影响Fig.19 The effect of the long to short axis ratio on the attitude deflection of the projectile

4 结论

本文结合双层间隔薄钢板斜贯穿实验，通过对TE型弹体贯穿过程、靶板破坏失效模式与弹体受力特征的物理作用过程分析，开展了TE型弹体姿态偏转机理研究。得到如下主要结论：

1)TE型弹体贯穿薄靶的过程可分为弹体头部压入阶段、头部贯穿阶段、过渡阶段、弹身贯穿阶段；基于一定假设，依据刚体运动学规律和虚功原理，建立了分段式TE型弹体斜贯薄板剩余速度及偏转理论分析模型。

2)依据文献[38]中的实验及模拟结果对理论模型的可靠性进行验证，得出本文提出的理论模型能够实现对TE型及E型弹体初始倾角小于60°时，低速斜贯穿薄靶工况下弹体姿态偏转与剩余速度的预测。

3)随着TE型弹体撞击速度的增加，弹体姿态偏转角度呈现指数型减少趋势；TE型弹体姿态偏转量随着弹体初始倾角的增大而增大；TE型弹体结构设计中弹体质心越靠前弹体姿态越稳定。

4)由于TE型弹体结构的非对称性，相同初始条件下，TE型弹体以不同的翻滚角撞击靶板时，弹体姿态偏转角度不同，=0°时较=90°时弹体姿态偏转角度更大。

5)TE型弹体椭圆截面长短轴之比作为TE型弹体的一个重要特征，对弹体姿态偏转具有一定影响，当=0°时，随着长短轴之比增大，弹体姿态偏转角度随之增大；当=90°时，随着长短轴之比的增大，弹体姿态偏转角随之减小。

本文主要研究了TE型弹体斜贯穿薄靶的姿态偏转问题，并进行了参数影响分析，关于弹体侵彻弹道、侵彻性能及毁伤能力的问题，后续将开展相关研究。

[1] YAKUNINA G Y. Characteristic features of the high-velocity motion of bodies in dense media[J].Journal of Applied Mathematics and Mechanics，2012，76(3):310-323.

[2] BEN-DOR G，DUBINSKY A，ELPERIN T.Shape optimization of high-speed penetrators: a review[J].Central European Journal of Engineering，2012，2(4):473-482.

[3] BANICHUK N V，RAGNEDDA F，SERRA M. Probabilistic approach for shape optimization problems in contact mechanics[J].Structural and Multidisciplinary Optimization，2011，43(1): 99-106.

[4] 杜忠华，朱建生，王贤治，等.异型侵彻体垂直侵彻半无限靶板的分析模型[J].兵工学报，2009，30(4):403-407.

DU Z H，ZHU J S，WANG X Z，et al.Analytical model on non-circular penetrator impacting semi-infinite target perpendicularly[J].Acta Armamentarii，2009，30(4):403-407. (in Chinese)

[5] 高光发，李永池，刘卫国，等.长杆弹截面形状对垂直侵彻深度的影响[J].兵器材料科学与工程，2011，34(3):5-8.

GAO G F，LI Y C，LIU W G，et al. Influence of the cross-section shapes of long rod projectile on the vertical penetration depth[J].Ordnance Material Science and Engineering，2011，34(3):5-8. (in Chinese)

[6] GUO C，QIAN J，GU W，et al.Penetration characteristics of a penetrator with triangular cross-section impacting semi-infinite targets[J].Mechanics Based Design of Structures and Machines，2020(1):1-14.

[7] DONG H，WU H，LIU Z，et al.Penetration characteristics of pyramidal projectile into concrete target[J].International Journal of Impact Engineering，2020，143：103583.

[8] 杜忠华，曾国强，余春祥，等.异型侵彻体垂直侵彻半无限靶板试验研究[J].弹道学报，2008，20(1):23-25.

DU Z H，ZENG G Q，YU C X，et al.Experimental research of novel penetrator vertically penetrating semi-infinite target [J].Journal of Ballistics，2008，20(1):23-25. (in Chinese)

[9] 王文杰，张先锋，邓佳杰，等.椭圆截面弹体侵彻砂浆靶规律分析[J].爆炸与冲击，2018，38(1):164-173.

WANG W J，ZHANG X F，DENG J J，et al.Analysis of projectile penetrating into mortar target with elliptical cross-section[J].Explosion and Shock Waves，2018，38(1):164-173. (in Chinese)

[10] 刘子豪，武海军，高旭东，等.椭圆截面弹体侵彻混凝土阻力特性研究[J].爆炸与冲击，2019，39(2):135-141.

LIU Z H，WU H J，GAO X D，et al.Study on the resistance characteristics of elliptical cross-section projectile penetrating concrete[J].Transactions of Beijing Institute of Technology，2019，39(2):135-141.(in Chinese)

[11] DONG H，LIU Z，WU H，et al.Study on penetration characteristics of high-speed elliptical cross-sectional projectiles into concrete[J].International Journal of Impact Engineering，2019，132:103311.

[12] DAI X，WANG K，LI M，et al.Rigid elliptical cross-section ogive-nose projectiles penetration into concrete targets[J].Defence Technology，2021，17(3): 800-811.

[13] BACKMAN M E，GOLDSMITH W.The mechanics of penetration of projectiles into targets[J].International Journal of Engineering Science，1978，16(1):1-99.

[14] ZUKAS J A. Impact dynmics[M].New York，NY，US：John Wiley & Sons，1981.

[15] ZUKAS J A. High velocity impact dynamics[M].New York，NY，US：John Wiley & Sons，1990.

[16] ANDERSON JR C E，BODNER S R.Ballistic impact: the status of analytical and numerical modeling [J]. International Journal of Impact Engineering，1988，7(1): 9-35.

[17] CORBETT G，REID S，JOHNSON W.Impact loading of plates and shells by free-flying projectiles:a review[J].International Journal of Impact Engineering，1996，18(2):141-230.

[18] GOLDSMITH W.Non-ideal projectile impact on targets[J].International Journal of Impact Engineering，1999，22(2/3):95-395.

[19] 钱伟长.穿甲力学[M].北京：国防工业出版社，1984.

QIAN W C. Armor piercing mechanics[M].Beijing：National Defense Industry Press，1984.(in Chinese)

[20] ZENER C, PETERSON R E.Mechanism of armor penetration No.A:[R].710/492 Watertown, MA, US: Watertown Arsenal，1943.

[21] AWERBUCH J，BODNER S.An investigation of oblique perforation of metallic plates by projectiles[J].Experimental Mechanics，1977，17(4):147-153.

[22] ZAID M，PAUL B.Mechanics of high speed projectile perforation[J].Journal of the Franklin Institute，1957，264(2):117-126.

[23] BΘRVIK T，OLOVSSON L，DEY S，et al.Normal and oblique impact of small arms bullets on AA6082-T4 aluminium protective plates[J].International Journal of Impact Engineering，2011，38(7):577-589.

[24] GOLDSMITH W，FINNEGAN S.Normal and oblique impact of cylindro-conical and cylindrical projectiles on metallic plates[J].International Journal of Impact Engineering，1986，4(2):83-105.

[25] GUPTA N，MADHU V.Normal and oblique impact of a kinetic energy projectile on mild steel plates[J].International Journal of Impact Engineering，1992，12(3):333-343.

[26] GUPTA N，MADHU V.An experimental study of normal and oblique impact of hard-core projectile on single and layered plates[J].International Journal of Impact Engineering，1997，19(5/6):395-414.

[27] 黄涛，吴卫国，李晓彬，等.截锥形弹体斜穿甲花瓣型破坏模型[J].振动与冲击，2010，29(2):125-127.

HUANG T，WU W G，LI X B，et al.Oblique armor-piercing effect of a truncated cylindroconical projectile[J].Journal of Vibration and Shock，2010，29(2):125-127.(in Chinese)

[28] 徐双喜，吴卫国，李晓彬，等.锥头弹小斜角侵彻薄板剩余速度理论分析[J].弹道学报，2010，22(3):58-62.

XU S X，WU W G，LI X B，et al.Theoretical analysis on residual velocity of conical projectile after penetrating thin plate at low oblique angle[J].Journal of Ballistics，2010，22(3):58-62. (in Chinese)

[29] RECHT R F，IPSON T W.Ballistic perforation dynamics [J].Journal of Applied Mechanics，1963，30(3):384-390.

[30] RECHT R F，YATTEAU J.Multiple plate penetration modelling for deforming and yawing ballistic penetrators which lose mass[C]∥Proceedings of the 7th International Symposium on Ballistics.Hague，the Netherlands: International Ballistics Committee，1983:271-280.

[31] LI K，GOLDSMITH W. An analytical model for tumbling projectile perforation of thin aluminum plates[J].International Journal of Impact Engineering，1996，18(1):45-63.

[32] LI K，GOLDSMITH W.A phenomenological model for perforation of moderately thick plates by tumbling projectiles [J].International Journal of Solids and Structures，1996，33(24): 3561-3575.

[33] LI K，GOLDSMITH W.Perforation of steel and polycarbonate plates by tumbling projectiles[J]. International Journal of Solids and Structures，1997，34(35/36):4581-4596.

[34] CHEN X，LI Q，FAN S.Oblique perforation of thick metallic plates by rigid projectiles[J].Acta Mechanica Sinica，2006，22(4):367-376.

[35] DENG Y，LI J，JIA B，et al.Numerical study of failure modes and crack propagation in 2A12 aluminum target against blunt-nosed projectile at low yaw angle[J].Strength of Materials，2016，48(6): 834-849.

[36] IQBAL M，SENTHIL K，MADHU V，et al.Oblique impact on single，layered and spaced mild steel targets by 7.62 AP projectiles[J].International Journal of Impact Engineering，2017，110:26-38.

[37] 杜华池，张先锋，刘闯，等.弹体斜侵彻多层间隔钢靶的弹道特性[J].兵工学报，2021，42(6)：1204-1214.

DU H C，ZHANG X F，LIU C，et al. Trajectory characteristics of projectile into steel target with multi-layer space structure[J].Acta Armamentarii，2021，42(6)：1204-1214. (in Chinese)

[38] 王浩，武海军，闫雷，等.椭圆横截面弹体斜贯穿双层间隔薄钢板失效模式[J].兵工学报,2020,41(增刊2)：1-11.

WANG H，WU H J，YAN L，et al. Failure mode of oblique perforation of truncated ogive-nosed projectiles with elliptic cross-section into double-layered thin steel plate with gap space[J].Acta Armamentarii，2020，41(S2)：1-11. (in Chinese)

[39] GOLDSMITH W，TAM E，TOMER D.Yawing impact on thin plates by blunt projectiles[J].International Journal of Impact Engineering，1995，16(3):479-498.

[40] ZHANG T.Rupture of thin ductile tubes by oblique impact of flat-nosed missiles:analysis[J].International Journal of Impact Engineering，1998，21(7):541-570.