非对称类椭圆截面弹体斜贯穿铝靶数值模拟研究

岳胜哲，陈 利，张晓伟，李元龙，张庆明

(1.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；2.北京航天长征飞行器研究所， 北京 100076)

1 引言

近年来，异型截面弹体的设计与研发受到了各军事强国的关注。异型截面弹体是指截面形状非圆形的弹体，目前国内外科研人员对异型截面弹体的研究主要集中于弹体截面形状对弹体侵彻能力的影响。杜忠华通过对截面形状为圆形、矩形、三角形的钨合金弹体在不同初速度下侵彻4340钢靶的实验研究，发现在截面面积相等的情况下，弹体的侵彻深度由大到小依次为三角形、矩形和圆形。袁焘等开展了圆形、三角形、正方形、十字形和刻槽形等5种截面弹芯垂直侵彻半无限靶板的实验研究，发现3种异型截面相对于圆形弹芯都具有更高的穿甲效率，其中十字型效率最高。王皓对类椭圆截面侵彻混凝土的弹道特性进行了模拟研究，发现了弹丸的侵彻深度与截面的特征系数成反比关系。刘子豪研究了椭圆截面弹体侵彻混凝土过程中的受力特性，发现在相同速度下弹体侵深随着椭圆截面的长短轴之比的增大而增大。王文杰等研究了椭圆截面弹体侵彻混凝土靶的规律，并基于空腔膨胀理论建立了弹体的受力模型。Bless通过对比研究发现，临界速度下刚性非对称侵彻体侵彻性能更优，超过临界速度优势不再明显。Littlefield等使用数值模拟的方法研究了5种非对称截面形状长杆弹，发现等面积条件下截面形状对侵彻深度影响最大不超过4%。

为进一步扩展对异型弹体截面形状的研究，获得具有更好侵彻性能的弹体。本文提出弹体采用非对称类椭圆截面形状，在传统尖卵型弹体的基础上对弹体截面进行非对称类椭圆截面变形设计，并对其对铝靶的贯穿过程展开研究，系统地讨论弹体的截面形状不对称性对弹体弹道极限速度、弹体姿态和弹体质心运动的影响。

2 有限元模型建立与验证

2.1 仿真模型参数设置

参考文献[13]的实验条件，建立35 g弹体斜贯穿靶板的仿真模型，取弹体半径=6.5 mm，长径比为5，卵形头部系数CRH为3，靶板尺寸为250 mm×250 mm×2 mm。利用ANSYS-workbench软件对仿真弹体进行网格划分，采用三维实体单元对模型进行有限元离散。靶板采用中心加密画法，加密区域网格尺寸设置为0.2 mm×0.2 mm，如图1所示，靶板边界固支。使用Autodyn软件对弹体贯穿靶板过程进行仿真，单元算法设置为拉格朗日算法，单位制设置为mm-mg-ms。

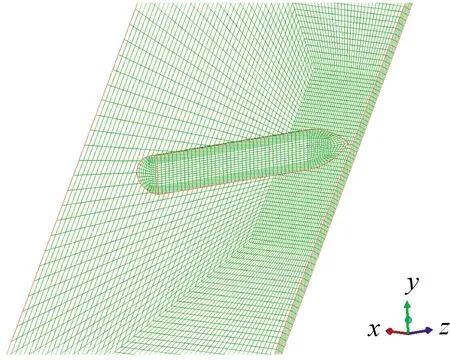
图1 弹靶网格三维模型示意图

弹体材料为38CrSi，采用刚体模型，密度为8.73 g/cm。靶板材料为铝合金，靶板的强度与失效模型均使用Johnson-Cook模型。其屈服应力表达式为：

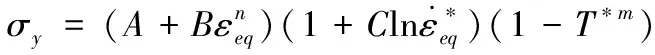
(1)

式(1)中，、、、、分别为静态屈服强度、硬化系数、应变率系数、温度软化指数、硬化指数。

单元毁伤准则为：

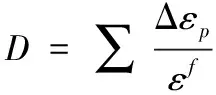
(2)

其中断裂应变为：

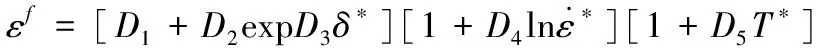
(3)

式(2)～(3)中：-为断裂常数；等于1即为单元发生破坏。靶板材料参数取自文献[14]，如表1所示，弹体材料参数取自软件数据库。

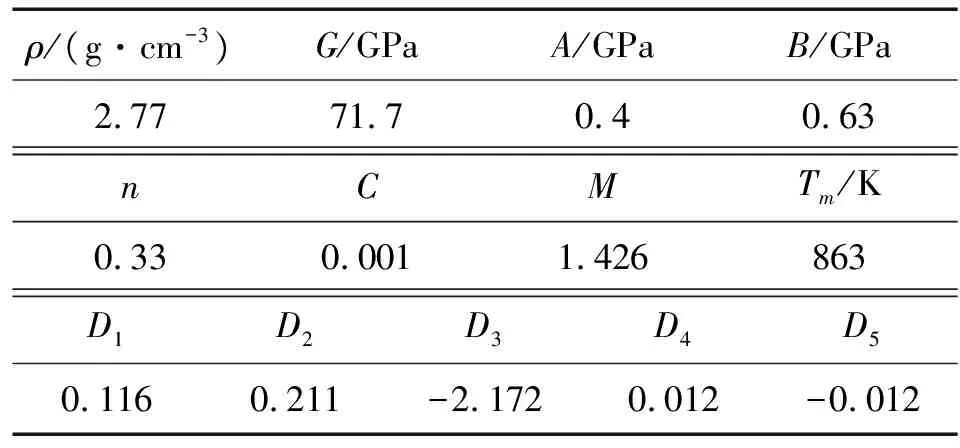
表1 靶板材料参数Table 1 Material parameters of target plate

2.2 模型有效性验证

采用上述模型及参数，对文献[13]中弹体正贯穿单层铝板实验进行仿真，仿真得到不同初始速度下卵型头部弹体正贯穿铝靶的剩余速度和实验结果，如表2所示。

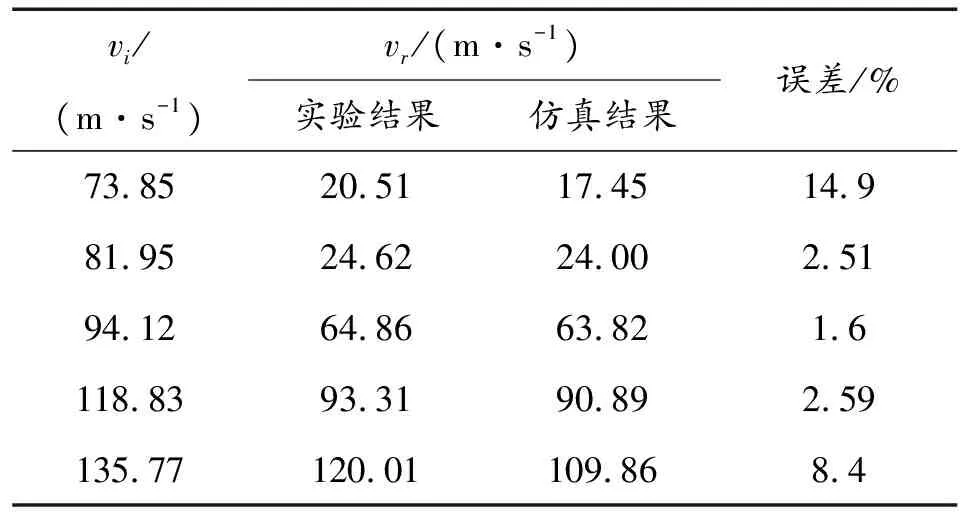
表2 弹体正侵彻靶板剩余速度仿真结果与实验结果Table 2 Comparison between simulation and experimental results of projectile body penetrating the target plate

使用Recht提出的弹道极限速度公式对所得速度值进行拟合，拟合曲线如图2。其公式为：

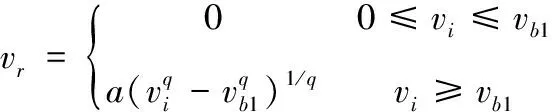
(4)

式(4)中：为弹体剩余速度；为弹体初始速度；1为弹道极限速度；为数据拟合参数;对于花瓣形破坏的靶板，取=1。使用最小二乘法拟合得到参数和弹道极限1，如表3所示。由表3的结果可知实验与仿真所得弹道极限速度误差仅为0.27。

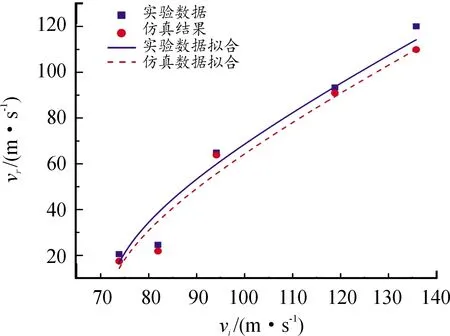
图2 弹道极限速度拟合曲线

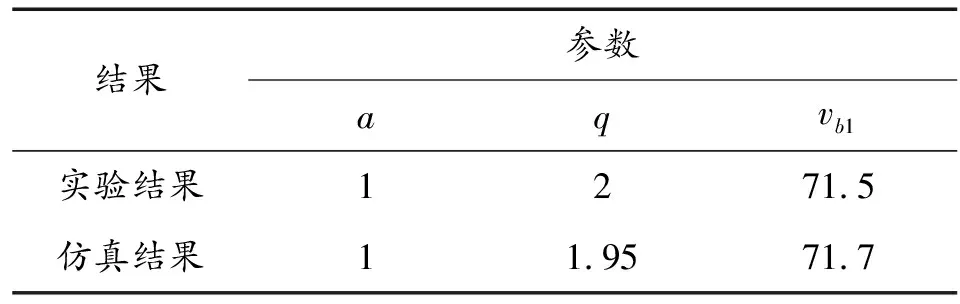
表3 模型参数及弹道极限Table 3 Model parameters and ballistic limit

图3给出了初速度为81.95 m/s与94.12 m/s情况下，弹体贯穿靶板的毁伤失效形貌。不同初速度条件下，弹体均对靶板产生了花瓣形破坏。其中，初速=81.95 m/s条件下,实验与数值模拟得到花瓣高度分别为4.89 mm、5.21 mm;初速=94.21 m/s条件下,实验与数值模拟得到花瓣高度分别为5.06 mm、4.63 mm。可见，靶板破坏形貌与花瓣高度基本相同，进一步说明了模型与参数设置的准确性。

图3 靶板的破坏形貌

2.3 非对称类椭圆截面弹型

在圆截面弹型的基础上，对其截面形状进行拉伸变形为非对称椭圆,如图4所示。取椭圆截面半短轴长=0.8，=1.25，将圆形截面拉伸变形为对称椭圆截面,随后在对称椭圆截面的基础上，将其上下两半短轴乘以不同的系数来改变其不对称度，即=,=。由椭圆面积公式=π=π(+)=π(+)可得，使+≡2即可保持其截面面积不变。因此，在弹体长度不变，弹体密度分布均匀的条件下，弹体质量、弹体质心在弹体轴线方向的位置也不会发生变化，则可定义弹体的不对称度为：

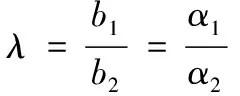
(5)

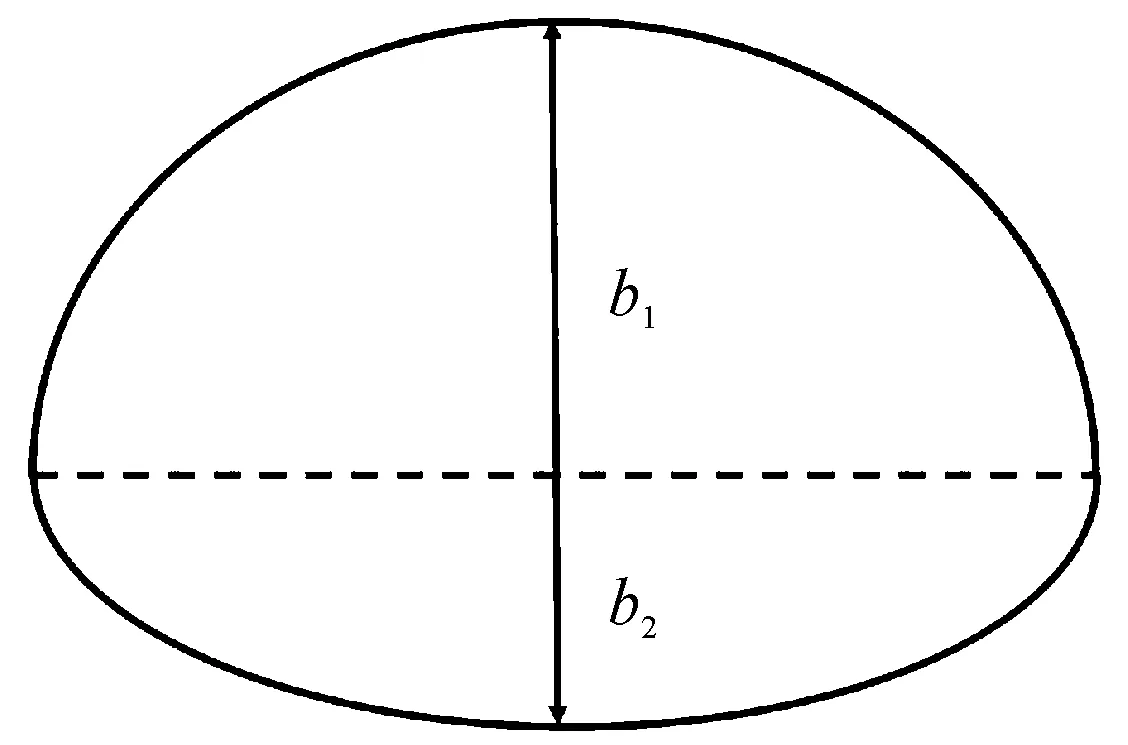
图4 非对称类椭圆截面形状示意图

通过改变不对称度得到5种不同弹型弹体，并加入传统圆截面弹型，如表4所示。对不同弹型分别在初速度为50 m/s、100 m/s、150 m/s、200 m/s、250 m/s条件下对30°倾斜靶板的贯穿过程进行仿真，弹靶实体模型如图5所示。

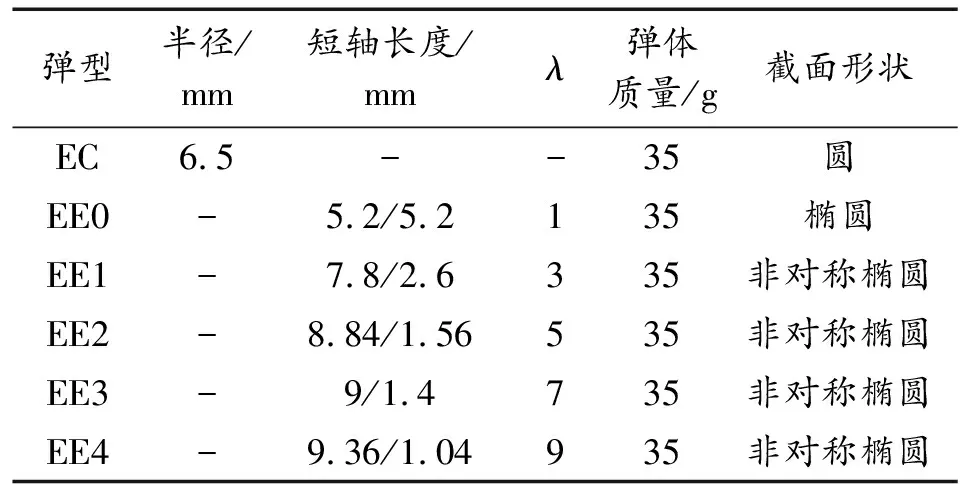
表4 弹体型号及参数Table 4 Projectile model and parameters

图5 弹靶初始实体模型示意图

3 仿真结果分析

3.1 截面不对称度对弹体弹道速度的影响

在50 m/s初速度条件下，各弹型均未贯穿靶板。其余初速度条件下，各型号弹体初速度与剩余速度关系如图6所示。

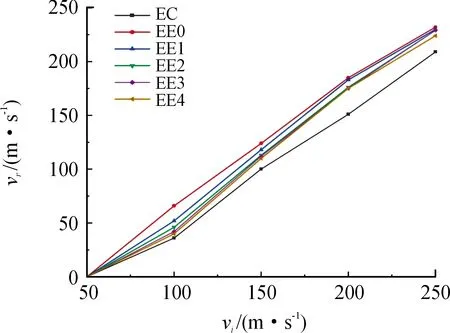
图6 不同对称度下弹体穿靶剩余速度曲线

由图6可以看出,不同初速度条件下，非对称类椭圆截面弹体剩余速度均高于传统圆截面弹型。且随着弹体不对称度的提高，弹体剩余速度变低。利用Recht公式，将各型弹体贯穿靶板后的初速度与剩余速度进行拟合，得到各非对称类椭圆截面弹型的弹道极限速度均低于传统圆截面(EC弹型弹道极限速度为72.1 m/s)。与传统圆截面弹型相比，非对称类椭圆截面弹体对靶板的穿透能力更强，随着不对称度的提高，非对称类椭圆截面弹体的弹道极限速度逐渐增高，接近传统圆截面弹体。不同截面不对称度弹体的弹道极限速度随不对称度变化如图7所示。

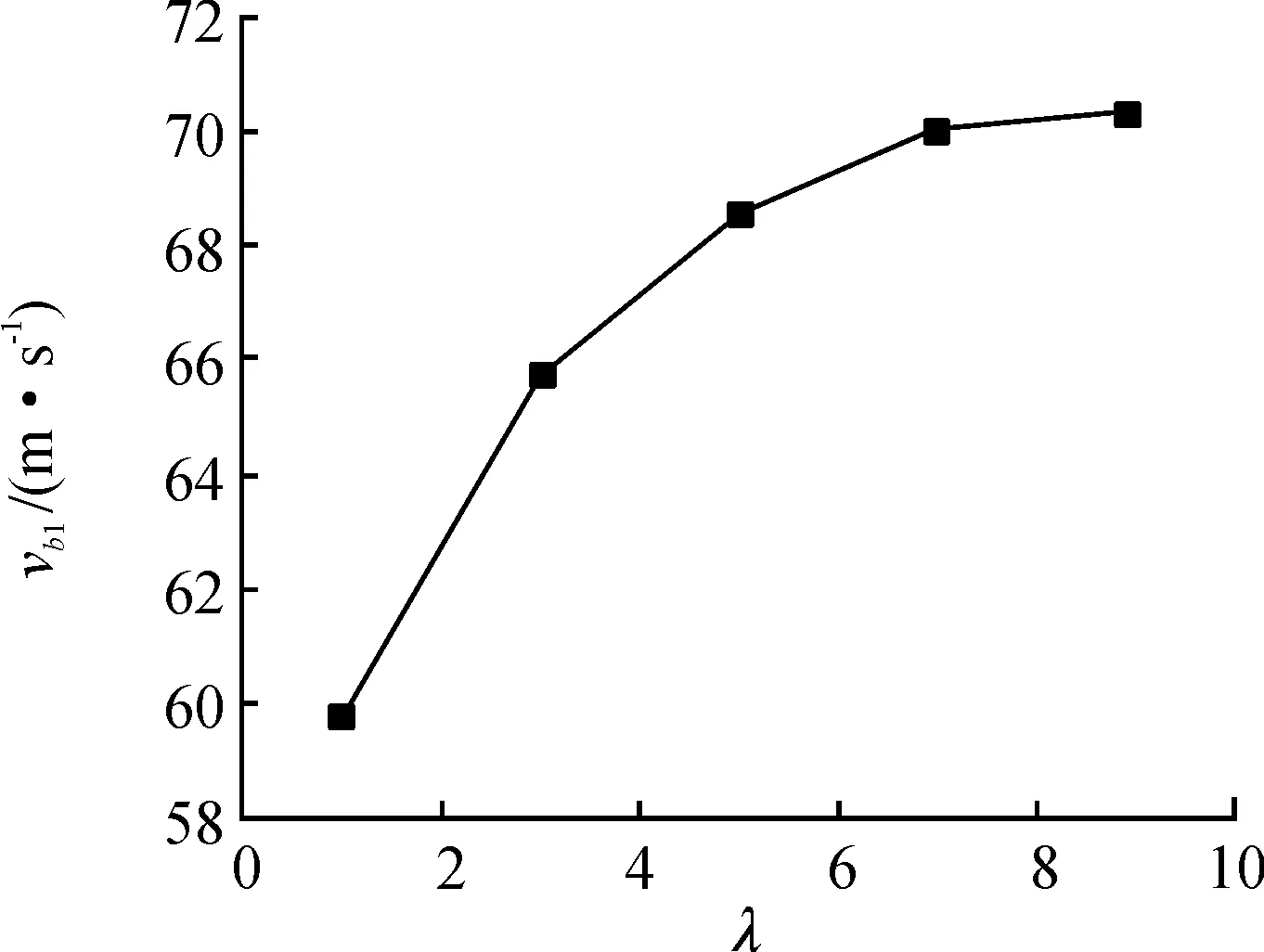
图7 弹道极限速度曲线

由图7可以看出，弹体的不对称度对弹体极限速度的影响规律明显，弹体的弹道极限速度随着弹体的不对称度提高而增大，随着不对称度的提高，不对称度对弹道极限速度的影响逐渐变低。这表明随着不对称度的增大，不同对称度在弹体对靶板产生破坏的过程中的能量耗散影响变小。在不对称度>5后，几乎可忽略弹体不对称度对弹体动能产生的影响。

3.2 截面不对称度对弹体偏转的影响

为描述弹体偏转角度的变化，选取弹体轴线上2点、，设2点纵坐标值为、，2点差值Δ=-，2点之间的距离为，则弹体偏转角度可表示为：

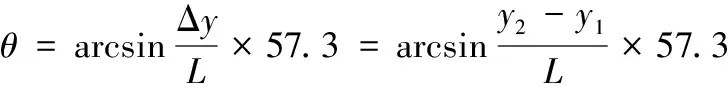
(6)

弹体偏转角度定义如图8所示，可以看出，当为正时弹体向上偏转，为负时弹体向下偏转。

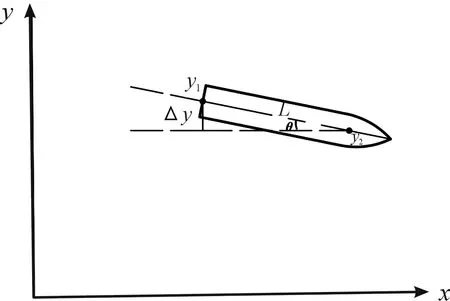
图8 弹体偏转角度定义示意图

图9给出了弹体在250 m/s初速度条件下的弹体偏转角度随时间变化。由图9可知，非对称类椭圆截面弹体偏转角度明显大于传统圆截面弹体，且与不对称度对弹道极限速度的影响相同，在不对称度<5时，弹体不对称度对弹体偏转角度影响较大，呈正相关；在不对称度>5之后，不对称度对弹体的偏转角度变化影响逐渐变小。

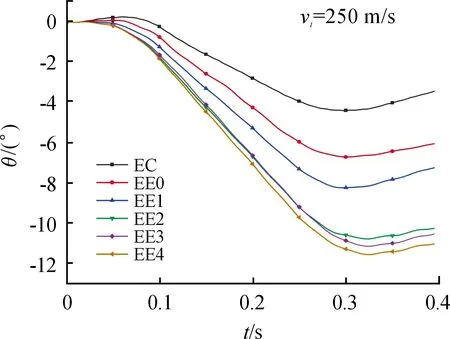
图9 弹体偏转角度随时间变化趋势曲线

图10给出了各型弹体出靶时刻偏转角度随弹体初始速度的变化。由图10可以看出，在不同初速度条件下，传统圆截面与不对称度为1、3、5的弹型偏转角度变化趋势相同，偏转角度随着截面不对称度的提高而增大。在不对称度>5后，弹体不对称度在各初速度条件下对弹体偏转角度影响减小。

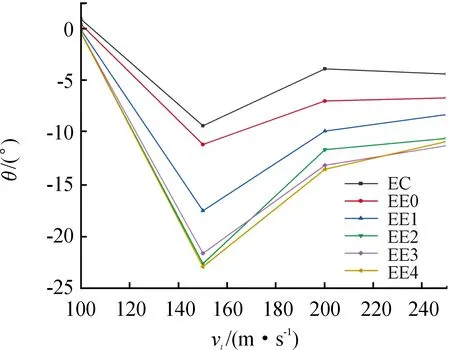
图10 不同初始速度条件下弹体出靶时刻偏转角度曲线

图11给出了弹体在250 m/s初速条件下，各弹型偏转角速度随时间的变化趋势。由图11可以看出，各不对称度弹体角速度随时间变化趋势相同，角速度随着弹体不对称度的提高而增大，表明随着弹体不对称度的增大，弹体所受非对称力作用越大。在不对称度>5后，弹体不对称度的变化对弹体偏转角速度影响显著性降低。

图11 弹体偏转角速度随时间变化趋势曲线

为进一步分析弹体截面形状对弹体偏转姿态的影响，图12给出了250 m/s条件下各弹型的角加速度变化趋势。由图12可知不同弹型的角加速度曲线变化趋势相同。为便于分析不对称度对弹体角加速的影响，将其划分为AB、BC、CD、DE、EF等5个阶段(其中B点、C点、D点、F点为弹体角加速度为0时刻)，图13分别给出了这5个阶段中的弹靶作用过程。

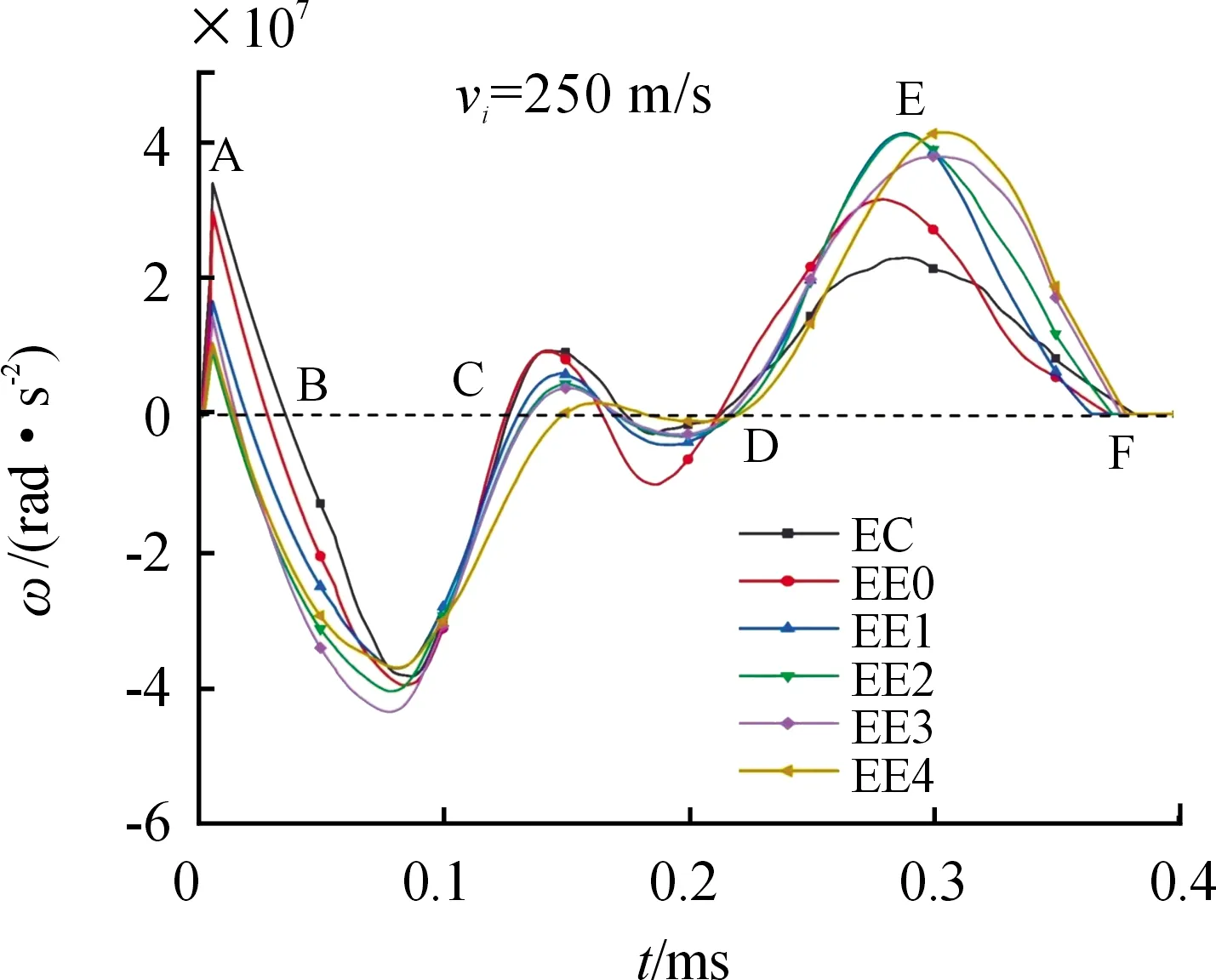
图12 弹体偏转角加速度随时间变化趋势曲线

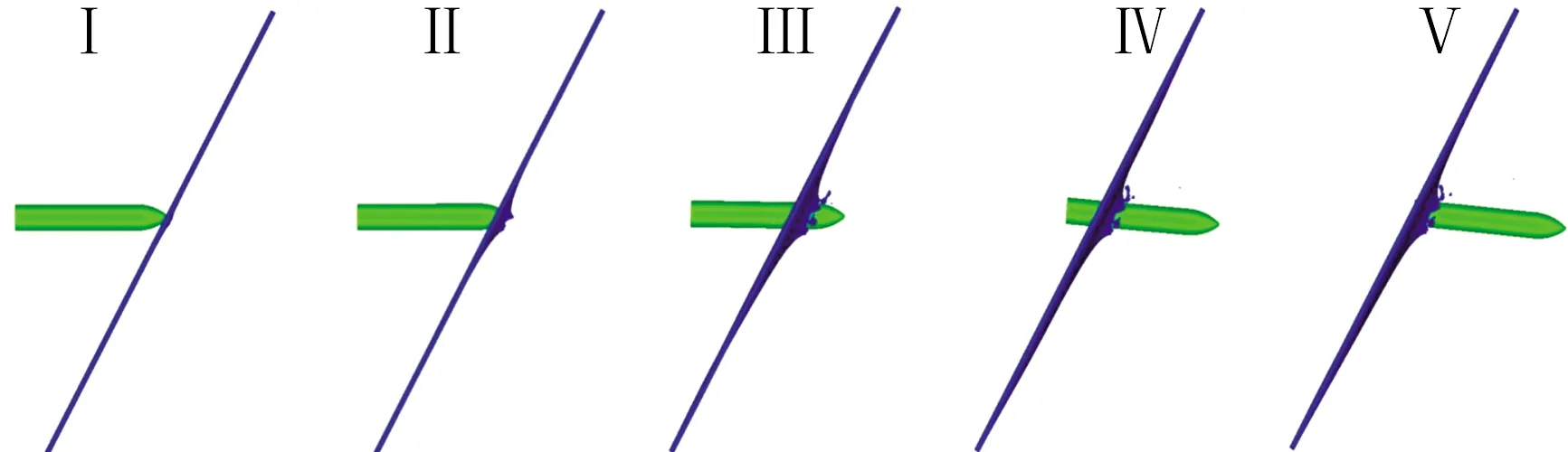
图13 弹体贯穿过程示意图

1) AB段， 弹体头部压入靶板，靶板形成凹陷但未被击穿。由于靶板倾斜，弹体在触靶时刻(图12中A点)受到逆时针方向转矩作用，可以看出，由于非对称弹体质心位置改变所产生的顺时针偏转力矩作用，非对称截面弹体所受逆时针方向转矩明显低于对称截面弹体。因此，非对称截面弹体在侵彻顺时针倾斜靶板时不易发生滑移,且弹体所受转矩大小随着弹体不对称度的增大而减小。

2) BC段，此时靶板被弹体击穿形成穿孔，弹体与靶板穿孔上沿接触面积逐渐减小，弹体受到靶板穿孔下沿接触力作用增强，弹体头部逐渐出靶，弹体所受顺时针方向转矩呈先增大后减小趋势，非对称截面弹体所受转矩小于对称截面弹体。

3) CD段，弹体偏转力矩达到C点后，弹体头部过靶，弹体持续向前侵彻，弹体与靶板穿孔上、下沿均有接触，且接触位置逐渐向弹体质心靠近，弹体所受转矩逐渐减小。此阶段弹体所受转矩只发生小幅度震荡。可以看出，随着弹体不对称度的提高，弹体转矩震荡幅度变小，此阶段非对称弹体姿态更加稳定。

4) DE阶段，弹体与靶板穿孔下沿发生脱离，弹体与靶板穿孔上沿接触位置位于弹体质心后方，使弹体受到逆时针方向转矩作用，随着弹体的向前侵彻，转矩逐渐增大。此阶段非对称弹体所受转矩明显高于传统圆截面弹体。

5) EF阶段，弹体逐渐与靶板穿孔上沿脱离，受到靶板上沿作用力减小，所受逆时针转矩逐渐降低。与ED段相同，此阶段非对称弹体所受转矩明显大于对称弹体，且随着不对称度的提升而增大。由于各弹型偏转角度不同，最终出靶时刻略有差异。

根据以上分析可知，不对称度对弹体所受转矩的影响和弹体与靶板的相互作用位置相关。在AB、BC段，即弹体头部与靶板相互作用阶段，弹体所受转矩大小随着弹体不对称度的增大而减小。在CD、DE、EF阶段，即弹身与靶板相互作用阶段，弹体所受转矩随着弹体不对称度的增大而增大。

3.3 弹体质心偏转轨迹分析

由于弹体的不对称度不同会使弹体质心在纵向平面内发生偏移，为方便对比弹体不对称度对质心偏转轨迹的影响，将各弹型质心置于同一初始点。图14为初速度在150 m/s和250 m/s情况下，各型弹体的质心的偏转轨迹。

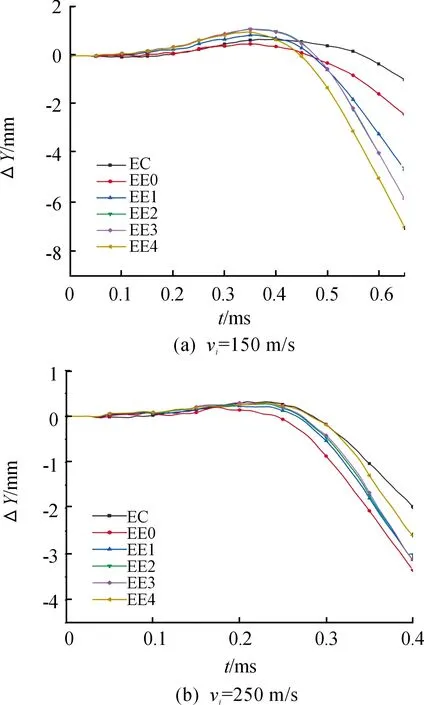
图14 初始速度为150 m/s和250 m/s时各弹型的质心偏转轨迹

由图14可以看出，弹体质心的向偏移量随着的弹体截面不对称度的增加而提高，不对称度越大，截面不对称度的变化对弹体偏转影响就越小。随着弹体初速度的提高，截面不对称度对弹体偏转影响变小，这是由于当弹体速度变高时，弹体受转矩作用时间减小，由截面不对称度引起弹体所受偏转力矩的变化对弹体的弹道偏转影响减少导致。

4 结论

1) 在截面面积与弹体质量相同的条件下，各非对称截面弹型贯穿铝靶的弹道极限速度均低于传统圆截面弹体。弹体截面不对称度越大，弹体弹道极限速度越高。

2) 弹体偏转角度与偏转角速度均随着不对称度的提高而增大。非对称截面弹体所受偏转力矩在弹体头部与靶板相互作用阶段随着不对称度的增大而减小，在弹身与靶板相互作用阶段随着不对称度的增大而增大。

3) 随着弹体初速度的增高，截面不对称度对弹体弹道偏转的影响逐渐变低。各型弹体弹道偏移轨迹趋同。