基于平衡算法的无坐力炮不平衡冲量研究

薛举元，陶 钢，王 鹏，徐 宁，李 召，任保祥

(1.南京理工大学 能源与动力工程学院， 南京 210094;2.中国人民解放军32381部队，北京 100072; 3.中国人民解放军63961部队，北京 100012)

1 引言

无坐力炮是一种滑膛无反后坐装置的火炮，在火炮发射时与闭膛炮有明显区别，即有气流从尾部喷管流出以抵消膛内气体推动弹丸时所产生的后坐力，同时，还是会产生不平衡冲量。不平衡冲量对单兵无坐力炮武器性能的安全性有较大影响，因此对无坐力炮在发射过程中的不平衡冲量进行理论计算和试验测量是十分必要的。

为了研究无坐力炮的不平衡冲量，文献[1]通过建立准两相流内弹道模型得到了无坐力炮的不平衡冲量随时间的变化规律；文献[2]通过有限元软件分析了平衡体对平衡炮不平衡冲量的影响；文献[3]研究了带状变燃速发射药对无坐力炮不平衡冲量的影响；文献[4]对影响单兵武器发射的不平衡冲量进行了分析；文献[5]得出了75 mm无坐力炮不平衡冲量与喷管结构的关系；文献[6]通过自行设计的试验，测得了某无坐力炮的不平衡冲量。文献[7]建立了无坐力炮的一维两相流内弹道模型，但未对不平衡冲量进行研究。

本文利用经典无坐力炮平衡内弹道算法，建立了无坐力炮不平衡冲量的计算模型，并分别从弹丸挤进压力、堵片打开压力、火药弧厚、喷管面喉比等角度分析了初始设计参数对不平衡冲量的影响。通过该计算模型可以得到各设计参数对无坐力炮不平衡冲量的影响大小，可为无坐力炮不平衡冲量的优化提供了一定的参考。

2 数学物理模型

经典无坐力炮平衡内弹道算法将内弹道过程划分为前期、第一时期、第二时期这3个不同时期。这3个时期之间是相互连接的，前期的最终结果是第一时期的起始条件，第一时期的最终结果为第二时期的起始条件。按顺序分别作出各阶段的解，并在后两个过程中加入不平衡的计算。另外应用经典无坐力炮平衡内弹道算法还需作出如下简化和假设：

1) 火药燃烧在平均压力下进行且服从正比燃速定律；

2) 在整个内弹道过程中，火药力、余容及绝热指数均为常数；

3) 因点火药在整个装药能量中占比很小，将点火药质量折合成主装药质量考虑；

4) 弹丸挤进膛线和堵片打开是瞬时进行的，分别以挤进压力和堵片打开压力表示弹丸挤进和堵片打开。

2.1 无坐力炮内弹道方程

..前期

在这一时期中，火药一直在容积为的药室中燃烧，容积内的压力由点火药压力升高到弹丸起动压力，求出此阶段结束后的火药形状尺寸参数、、。

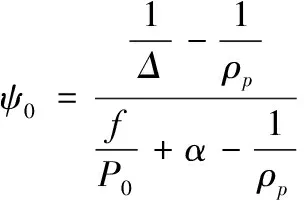
(1)

(2)

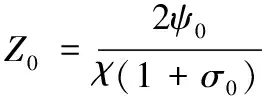
(3)

得到的、、既是前期计算的最终结果，也是第一时期的起始条件。

..第一时期计算

在这一时期中，弹丸达到挤进压力并开始向前运动而堵片未打开。在一般无坐力炮经典内弹道方程组中，共有6个方程，有、、、、、及七个变量，在这7个变量中，只有和的边界是已知的，即的范围是到1，的范围是到1，设=-作为自变量，结合一般无坐力炮经典内弹道方程组分别得出函数、、、的表达式：

1) 弹丸速度方程

(4)

2) 几何燃烧定律方程

=++

(5)

式中=

3) 弹丸行程方程

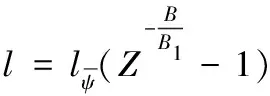
(6)

4) 压力方程

(7)

上述式中：为弹丸运动速度；为火药相对已燃厚度；为身管截面积；为发射药的压力全冲量；′为第一时期次要功系数；为弹丸质量；为火药相对已燃质量；和为火药形状特征量；为弹丸运动行程；为膛内平均压力；为火药力；为火药质量。

在这一时期中，当药室底部压力达到堵片打开压力时，记下此时刻的、、、并带入第二时期的计算。

..第二时期计算

1) 弹丸速度方程

(8)

2) 几何燃烧定律方程

(9)

式中=(1+2)

3) 气体流量方程

(10)

4) 弹丸行程方程

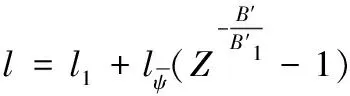
(11)

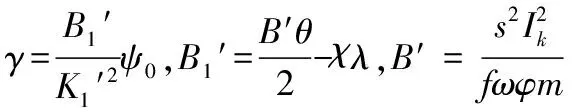
5) 压力方程

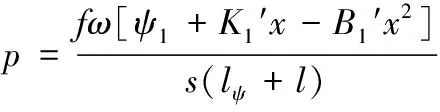
(12)

上述式中：″为第二时期次要功系数；为流量损失系数；为喷管喉部面积；为流量系数。

2.2 不平衡冲量的计算

不平衡冲量是一个过程量，但在本文1.1中的内弹道方程组中只能得到-、-之间的关系，所以在进行不平衡冲量计算之前，还应解出-、-之间的对应关系。将求出的-曲线做出1-曲线进行如下的图解积分，计算与各值相应的值。由于当接近于0时，1将趋近于无穷大，所以在起始段应采用近似方法来处理。先将分成两段来处理，即

(13)

式中的′是按下式来确定的：

(14)

其中′2代表=0和=′之间的速度平均值，为了尽可能减小误差，必须在-曲线中取较小的′值，当′取得合适时，误差可以忽略不记。这样可以得出-、-之间的关系。

在第一时期中，弹底压力达到弹丸挤进压力并推动弹丸向前运动，则因弹丸运动所产生的后坐冲量为

(15)

式中:为第一时期弹底压力，为身管横截面积，′为第一时期次要功系数。

在第二时期中，当药室底部压力达到堵片打开压力时时，这时炮身的不平衡冲量由弹丸运动和喷管流出的气体共同作用，设沿炮轴朝向炮尾的方向为合力的正方向，则炮身受力如图1所示。

图1 第二时期炮身受力示意图

当弹丸以速度运动时，火药气体在药室压力的作用下流经喷管的喉部截面后膨胀，并在通过喷管外部截面后具有压强，这里气体未充分膨胀，所以比一般大气压强要大得多，忽略外界大气压对其的影响，在喷管出口截面气体的流出速度为。

将整个发射器看成是一个整体，根据内力作用下的系统各部分的动量等于外力冲量的力学原理对整个发射器进行分析[9]：

2) 外力作用下的冲量：在喷管外部截面中的气体压力冲量为-。

根据内力与外力的分析，得到

(16)

火药气体对炮身的作用力可以表示为：

(17)

则第二时期的不平衡冲量为

(18)

上述式中，″为第二时期的次要功系数；为流速损失系数；为流量修正系数；为喷管推力系数，它是绝热指数、的函数，其数值详见文献[10]；为喷管出口截面积；为喷管喉部截面积；为膛内总静压。

3 试验及计算结果分析

3.1 试验方案

试验现场布置如图2所示，将发射器放置在自制的炮架上，使发射器与滑块相固连，滑块可在滑轨上沿膛线方向前后自由移动。通过位移传感器测得发射器前后运动位移随时间的变化，对位移数据进行一阶求导得到发射器沿轴线的运动速度，再与运动质量相乘得到不平衡冲量。试验的初始参数如表1、表2所示，并在相同的工况下对无坐力炮的发射过程进行3次不平衡冲量的测量。

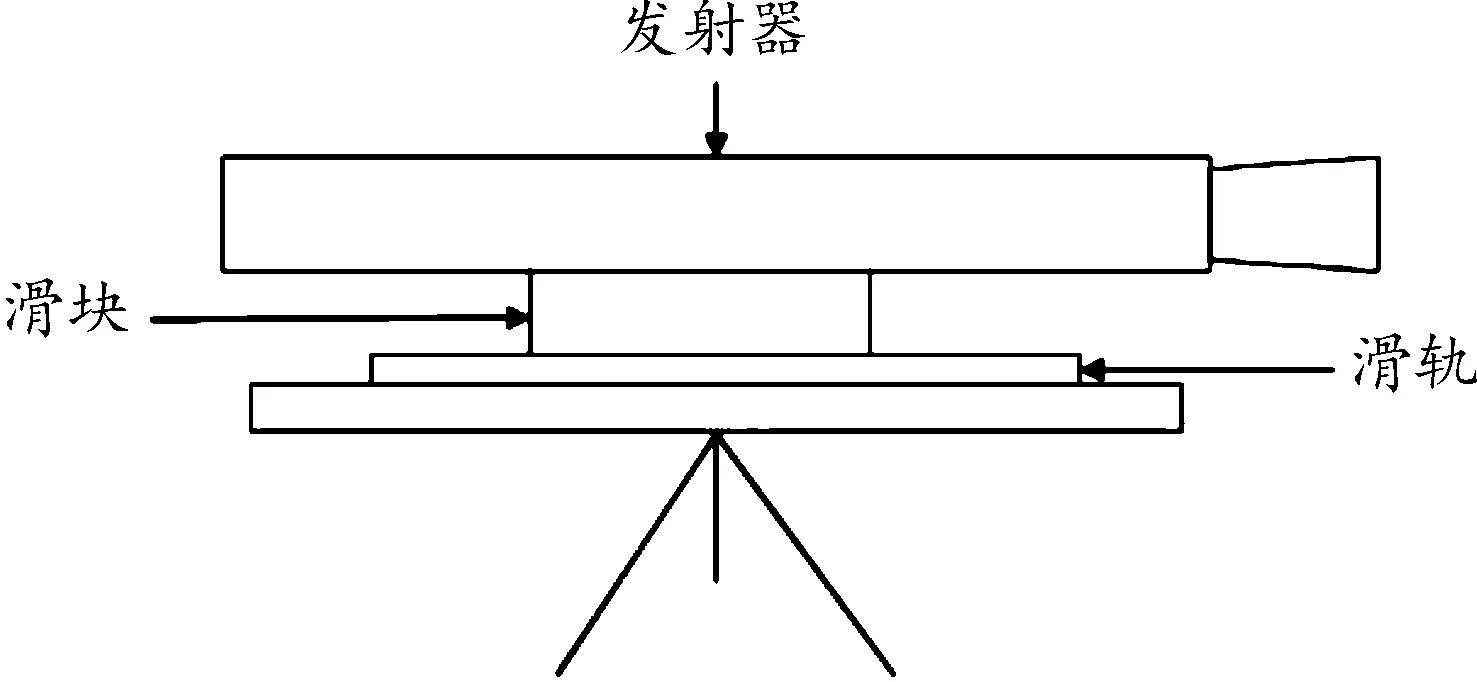
图2 不平衡冲量试验布置示意图

表1 火炮构造诸元参数Table 1 artillery structure elements

表2 火药装填参数Table 2 Conditions of gunpowder loading

3.2 计算结果分析

将上述表格中的火炮初始参数带入经典无坐力炮平衡内弹道方程，通过数值仿真计算，不平衡冲量计算结果与试验结果对比如表3所示。结果表明，通过此平衡内弹道得到的不平衡冲量I与试验结果符合较好，相对误差均在10%以内，可用于指导工程设计。

表3 不平衡冲量计算结果与试验结果Table 3 Comparison of calculated results and experimental resultsof unbalance impulse

4 初始设计参数对不平衡冲量的影响研究

在验证经典无坐力炮平衡内弹道算法合理可行之后，下面对某新型无坐力炮分别从弹丸挤进和堵片打开压力、火药弧厚、喷管面喉比等设计参数对其不平衡冲量进行分析。

4.1 弹丸挤进和堵片打开压力对不平衡冲量的影响

采取单一变量原则，在其他条件不变的情况下，根据2.1中的内弹道方程组分别计算当弹丸挤进压力为 4 MPa、5 MPa、6 MPa、7 MPa、8 MPa时的-、-、-、-的关系，再根据式(15)、式(18)计算出这5种工况下的不平衡冲量。计算结果如图3所示。

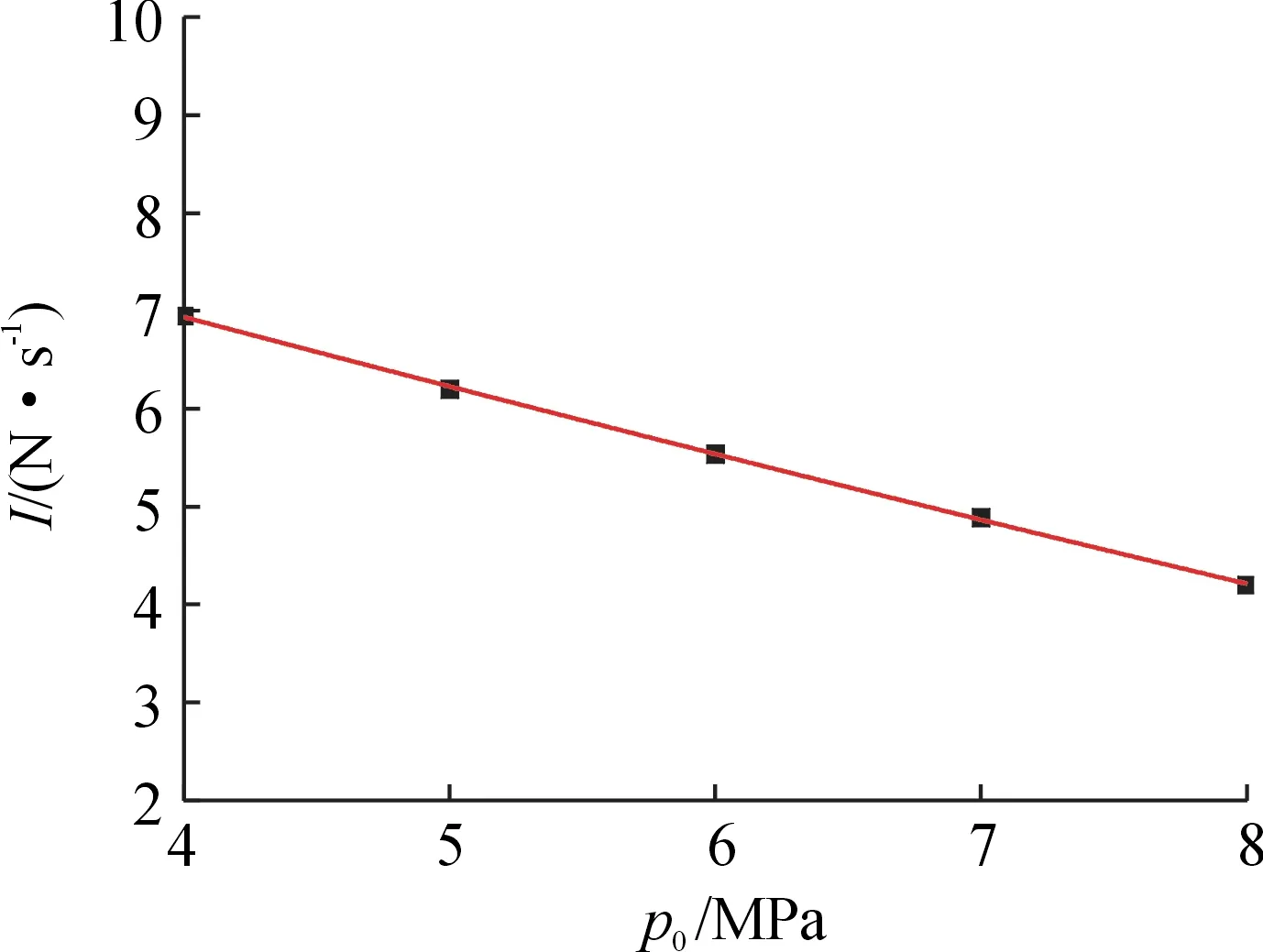
图3 不平衡冲量与弹丸挤进压力关系曲线

当弹丸挤进压力为7 MPa，在其他条件不变的情况下，计算堵片打开压力分别取8 MPa、9 MPa、10 MPa、11 MPa、12 MPa这5种工况下的不平衡冲量。计算结果如图4所示。

结合图3和图4可以看出，当弹丸挤进压力增大，逐渐接近于堵片打开压力时，不平衡冲量呈减小趋势；不平衡冲量随着堵片打开压力的增加而变大；弹丸挤进压力与堵片打开压力逐渐接近时，不平衡冲量呈减小趋势。

图4 不平衡冲量与堵片打开压力关系曲线

4.2 火药弧厚对不平衡冲量的影响

采取单一变量原则，在其他条件不变的情况下，根据2.1节中的内弹道方程组分别计算当火药弧厚分别为0.26 mm、0.28 mm、0.30 mm、0.32 mm、0.34 mm时的-、-、-、-的关系，再根据式(15)、式(18)计算出这5种工况下的不平衡冲量。计算结果如图5所示。

图5 不平衡冲量与火药弧厚关系曲线

由图5可以看出，火药弧厚越厚不平衡冲量越小。但由于火药弧厚对火炮膛压与炮口初速的影响较大，所以在满足膛压和初速指标的情况下，选用较厚的火药弧厚有利于不平衡冲量的下降。

4.3 喷管面喉比对不平衡冲量的影响

采取单一变量原则，在其他条件不变的情况下，根据2.1节中的内弹道方程组计算当喷管的面喉比分别为2、2.5、3.33、5、10时的-、-、-、-的关系，再根据式(15)、式(18)计算出这5种工况下的不平衡冲量。计算结果如图6所示。

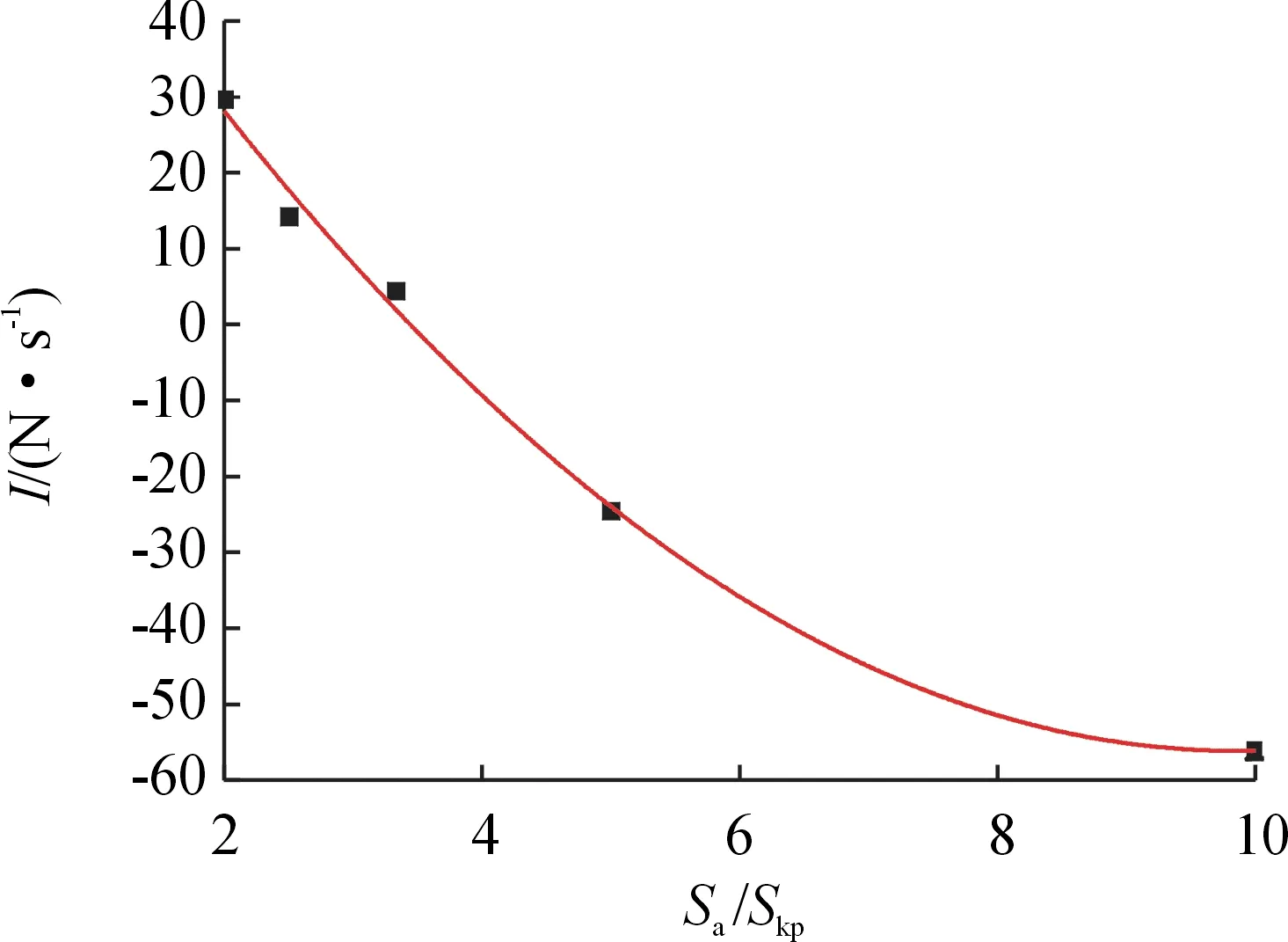
图6 不平衡冲量与喷管面喉比关系曲线

从图6可以看出喷管面喉比的变化对不平衡冲量的影响很大，随着面喉比的增大，不平衡冲量由后坐变为前冲，且变化幅度较大，这说明选择合适的面喉比在无坐力炮的不平衡力初期设计和试验中起着重要作用。

5 结论

1) 喷管面喉比是影响无坐力炮平衡的重要参数，对冲量影响较大，在火炮的设计及试验时应重点考虑并进行调试。

2) 弹丸挤进压力和堵片打开压力对无坐力炮冲量大小起着调节作用，当两压力值接近相等时，有利于减小不平衡冲量，在火炮试验的中后期应重点关注。

3) 在满足膛压和炮口初速的设计指标前提下，选用较厚的火药弧厚有利于降低不平衡冲量。

对影响冲量的参数进行合理的匹配，可优化某新型无坐力炮的平衡性能，并可对其他身管武器的平衡设计提供参考。