栅格环境下基于开阔视野蚁群的机器人路径规划

刘智飞，刘冬冬

(中国石油大学(华东) 石油工业训练中心， 山东 青岛 266580)

近年来机器人在生产制造业、物流、医疗、服务业等多个行业得到了广泛应用，不仅提高了生产效率，降低了生产成本，而且机器人可以代替人类从事劳力密集度高、危险、甚至人类无法完成的工作。路径规划技术是机器人的关键技术之一，是自主完成任务、实现智能化的前提，也极大地决定了机器人的工作效率[1]。因此，研究机器人路径规划问题对提高机器人工作效率、推动机器人广泛应用具有重要意义。

路径规划的主要任务是在满足设定约束的前提下，为机器人规划一条安全的最优路径，所谓最优路径是设定优化目标意义下的最优路径。根据环境信息的不同，路径规划可以划分为全局路径规划和局部路径规划[2]。全局路径规划适用于静态、已知的环境，这种情况下机器人可以获得先验地图。局部路径规划适用于动态的、未知的环境，机器人只能依靠自身传感器对周围环境进行探测，并实时进行路径规划。路径规划的核心问题是规划算法，路径规划方法可以分为传统路径规划算法和仿生路径规划算法，传统路径规划算法有人工势场法[3]、A*算法[4]、栅格法[5]等，仿生的的路径规划算法包括遗传算法、蚁群算法[6]、神经网络算法等。裴跃翔等[7]提出了嵌入筛选操作的遗传算法，一方面使用改进遗传算法在优化空间中细致搜索，另一方面使用标准遗传算法进行大范围开拓，将此算法应用于车身焊接路径规划中，得到了较好路径。胡平志等[8]为了解决复杂山地中机器人遇到的坡度问题，将坡度约束作为启发因素引入到蚁群算法中，得到了满足机器人坡度约束的山地路径。DAS等[9]提出了改进粒子群算法，同时将差分摄动速度算法融入到改进粒子群算法中，得到了适用于复杂环境的路径规划方法。由以上分析可知，在不同环境和应用背景下，具有不同的路径规划方法。在众多规划方法中，存在的共性问题是算法的规划能力，通过对算法不断改进而得到更加优化的路径是当前的研究热点。

本文针对栅格环境下的路径规划问题，提出了具有开阔视野的蚁群算法规划方法，对蚂蚁视野、邻域栅格、邻域中的可选栅格进行了重新定义，将开阔视野蚁群算法应用于栅格环境下的机器人路径规划，有效减小了路径长度并提高了路径平滑性。

1 环境模型与算法分析

1.1 栅格环境模型

栅格环境是指使用固定尺寸的栅格将机器人工作环境进行划分，机器人在行驶过程中以栅格为轨迹的基本单元。使用栅格分割完毕后，对栅格内的障碍物进行膨化处理，即当某栅格存在障碍物时，则障碍物膨胀而占满整个栅格[10]。如图1(a)为实际障碍物分布，膨化处理后如图1(b)所示。

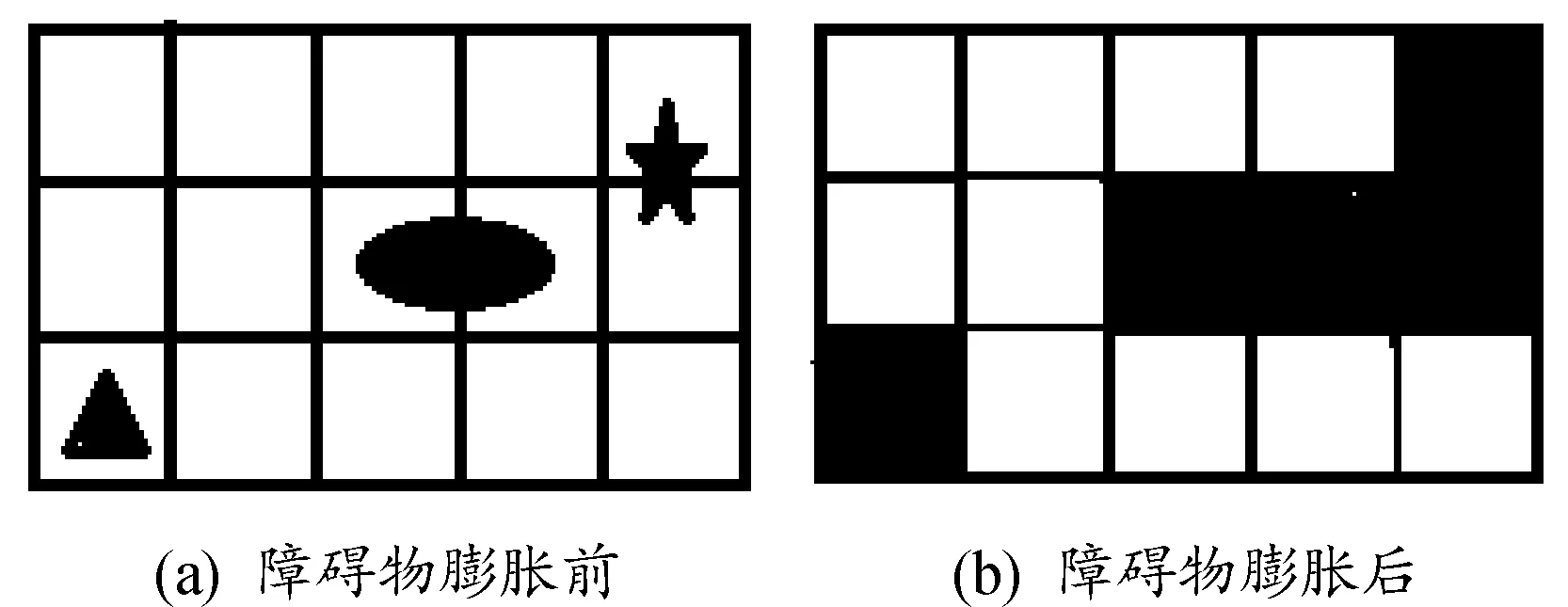
图1 障碍物膨化示意图

为了使机器人能够识别障碍物栅格和可自由行驶栅格，本文对不同类型的栅格赋予不同的属性值，将障碍物栅格的属性赋值为1，将自由栅格的属性赋值为0，从而得到机器人可以识别的0-1矩阵。以图1所示栅格环境为例，其对应的0-1矩阵为：

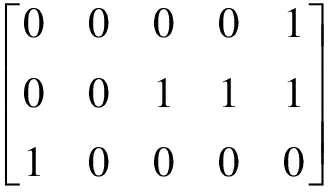
使用蚁群算法在栅格环境下进行路径规划时，将蚂蚁放置于起始栅格，蚂蚁通过在邻域自由栅格中不断选择，最终到达目标点。

1.2 标准蚁群算法

在标准蚁群算法中，蚂蚁依据启发信息和信息素浓度对邻域内自由栅格进行选择，蚂蚁对自由栅格的选择概率为[11]：

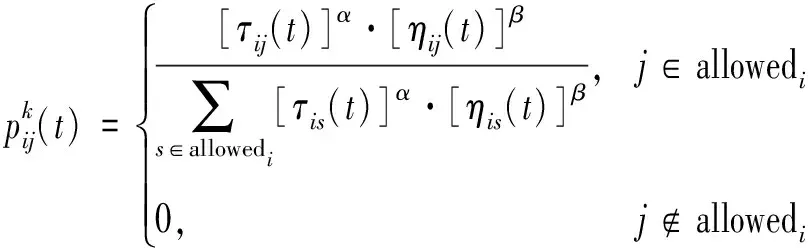
(1)

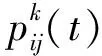
当蚁群算法完成一次迭代，则所有路径进行一次信息素浓度的更新，信息素浓度更新包括信息素挥发和信息素残留2个方面，即：

(2)

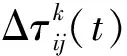
1.3 基于蚁群算法的路径规划分析

基于栅格地图的路径规划方法中，由于栅格地图的特点限制，主要存在4方向搜索和8方向搜索2种方法。其中4方向搜索主要指正上、正下、正左、正右4个方向的栅格，如图2(a)所示。8方向搜索主要指正上、正下、正左、正右、左上、左下、右上、右下8个方向的栅格，如图2(b)所示，图中圆圈所在栅格为当前栅格。

图2 不同的邻域搜索方法

在图2(a)所示的4方向搜索方法中，蚂蚁的可选栅格为邻域内的4个栅格，此时蚂蚁的角度分辨率为90°；在图2(b)所示的8方向搜索方法中，蚂蚁的可选栅格为邻域内的8个栅格，此时蚂蚁的角度分辨率为45°。由以上分析可知，当前基于栅格环境的蚁群算法中，蚂蚁的活动能力(即转角分辨率)被限制在90°或者45°，这意味着蚂蚁的活动能力受到了极大限制。

2 开阔视野蚁群算法

2.1 开阔视野设置方法及优势分析

为了提高蚂蚁活动的机动能力，提出了栅格环境下具有开阔视野的蚁群算法。其核心思想为：将蚂蚁的视野范围扩大1倍，在这种设置方式下，蚂蚁的邻域栅格由之前的8栅格变为24栅格，如图3所示。图中圆形所在栅格为当前栅格，实心圆点所在栅格为邻域栅格。

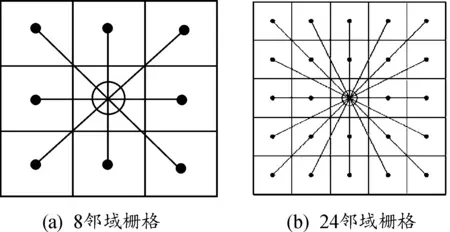
图3 不同视野蚂蚁的邻域栅格

蚂蚁的视野范围经过扩展以后，邻域栅格数量上的增加可以带来蚂蚁机动能力的提高。如前文所述，在8方向搜索方式中，蚂蚁运动的角度分辨率为45°；结合图3(b)可知，具有开阔视野的蚂蚁运动的角度分辨为22.5°，这意味着蚂蚁运动的灵活性得到了明显提高。

将开阔视野蚁群算法与传统的4方向搜索、8方向搜索进行对比，更加能够体现开阔视野蚁群算法的优势，以图4所示的情况为例进行说明。图4中S栅格为起点栅格，G栅格为目标栅格。

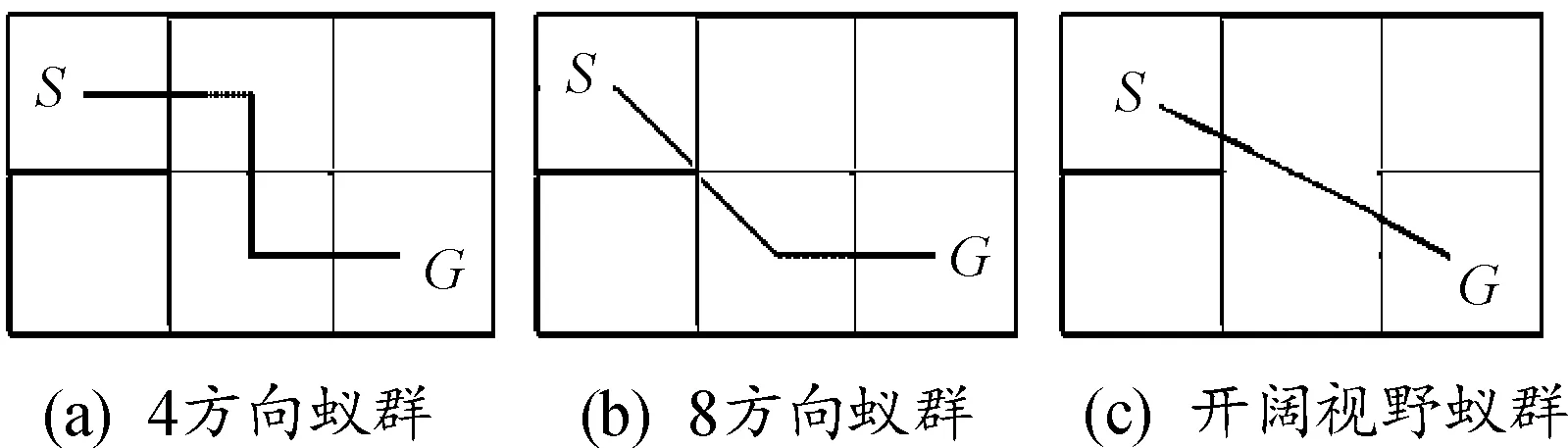
图4 不同蚁群的运动路径

对比图4中各种蚁群算法的规划路径，从转弯次数、路径长度、规划次数3个角度进行对比，结果如表1所示。设定栅格的边框长度为1。

表1 不同算法规划结果

结合表1和图4可以明确看出开阔视野蚁群算法的几点优势：① 路径转弯次数少，这意味着路径更加平滑；② 规划次数最少，这意味算法的规划效率最高；③ 所规划路径长度最短，可以有效减少机器人的行驶能耗。

2.2 邻域可选栅格的重新定义

按照开阔视野蚁群算法的邻域设置，传统关于可选栅格的定义不再适用，在此对邻域内的可选栅格进行重新定义。分析图5(a)中开阔视野蚁群的邻域栅格可知，可以将24个邻域栅格分为2类，一类是一步可到达的邻域栅格，如图5(a)中红色三角标出的栅格，此类栅格的可选栅格定义与传统一致，也即栅格中不存在障碍物时为可选栅格。另一类是两步可到达栅格，如图5(a)中黑色实心圆标出的栅格，当此类栅格自身为自由栅格且与蚂蚁间不存在障碍物遮挡时为可选栅格。

以图5(b)为例对第2类栅格的可选栅格进行解释，图5(b)中红色实心圆所在栅格为当前栅格，栅格1～5为其两步可达的邻域栅格，虽然栅格1～5均为自由栅格，但是由于栅格2、3、4与当前栅格的连线经过了障碍物，因此栅格2、3、4为不可选栅格，而栅格1、5与当前栅格的连线不经过障碍物，因此栅格1、5为可选栅格。

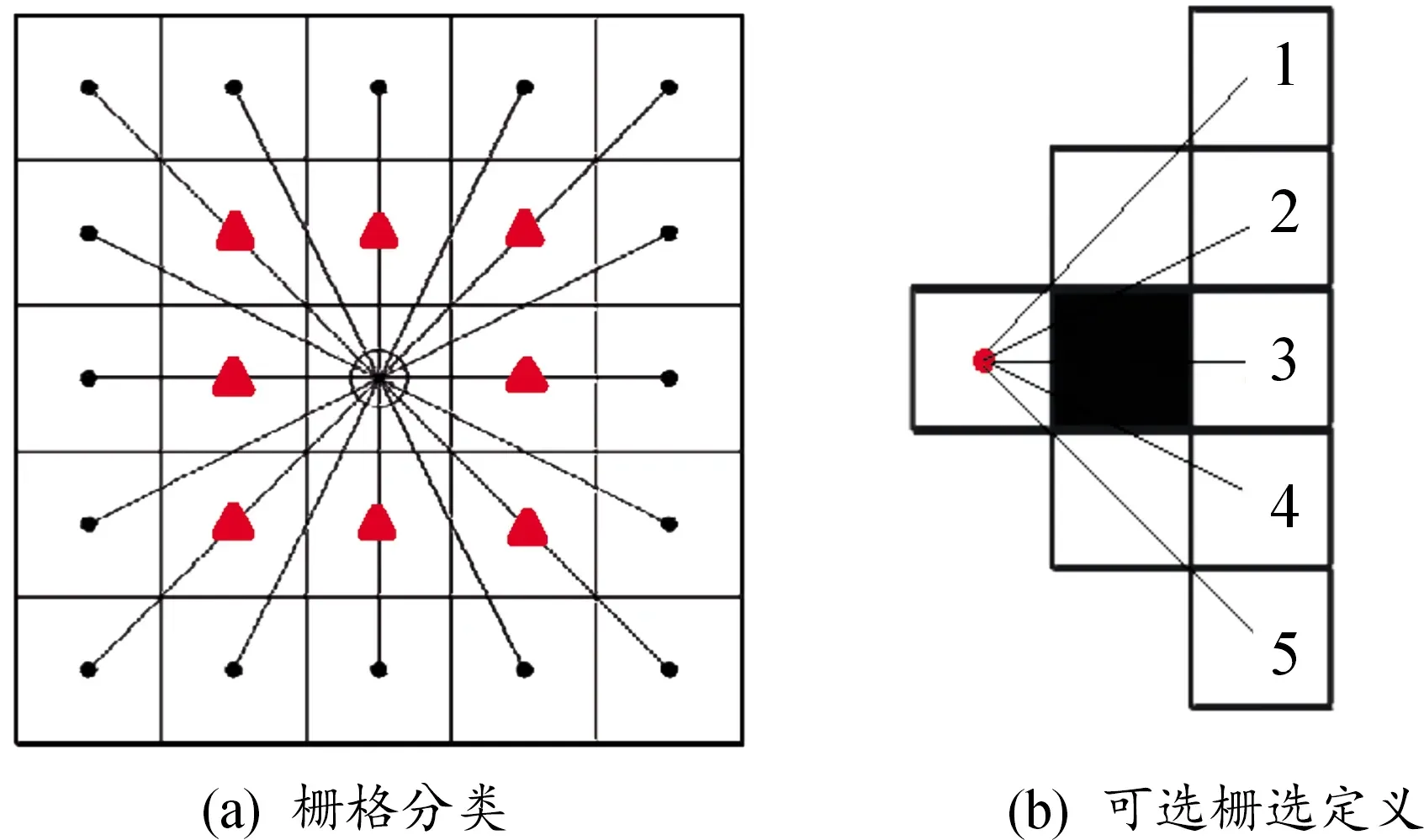
图5 开阔视野蚁群的可选栅格定义

2.3 栅格选择概率

按照2.2节可以确定当前栅格的可选栅格，而每个可选栅格的选择概率可以依据式(1)计算得到。在此需要明确的是，式(1)中的启发信息ηij(t)为：

(3)

式中：sjG为栅格j与目标栅格G之间的直线距离。

结合式(1)和式(3)计算各可选栅格的选择概率，选择概率最大的栅格为运动的下一栅格。

2.4 基于开阔视野蚁群算法的路径规划步骤

按照开阔视野蚁群算法原理，结合工作环境的栅格模型特点，制定基于开阔视野蚁群算法的路径规划步骤为：

步骤1设置开阔视野蚁群算法参数，包括蚂蚁规模、信息素因子、启发因子、信息素挥发系数、算法最大搜索次数等。

步骤2将所有蚂蚁放置在起点栅格。

步骤3蚂蚁按照2.1节方法确定邻域中的可选栅格，根据式(1)(2)(3)计算各可选栅格的选择概率，并选择概率最大的栅格作为下一栅格，每只蚂蚁重复执行步骤3直至到达目标栅格。

步骤4当所有蚂蚁到达目标栅格时，意味着算法完成一次迭代，此时迭代次数+1。

步骤5判断是否达到最大迭代次数，若否，则转至步骤2；若是，则输出最优路径，算法结束。

3 仿真验证

为了验证本文提出的开阔视野蚁群算法的规划效果，设置15×15和30×30 2种规模的栅格环境，同时使用开阔视野蚁群算法、传统的4向蚁群算法、8向蚁群算法进行路径规划。算法的参数设置为：蚂蚁数量为50，最大迭代次数为100，信息素因子为1.5，启发因子为6.0，挥发系数为0.4。计算环境为Windows 10、i5CPU、内存8 GB，仿真软件为Matlab2017。

为了减小随机因素的影响，同时使用3种算法在2个规模的栅格环境下进行10次路径规划，2种栅格环境下10次规划结果如图6所示。

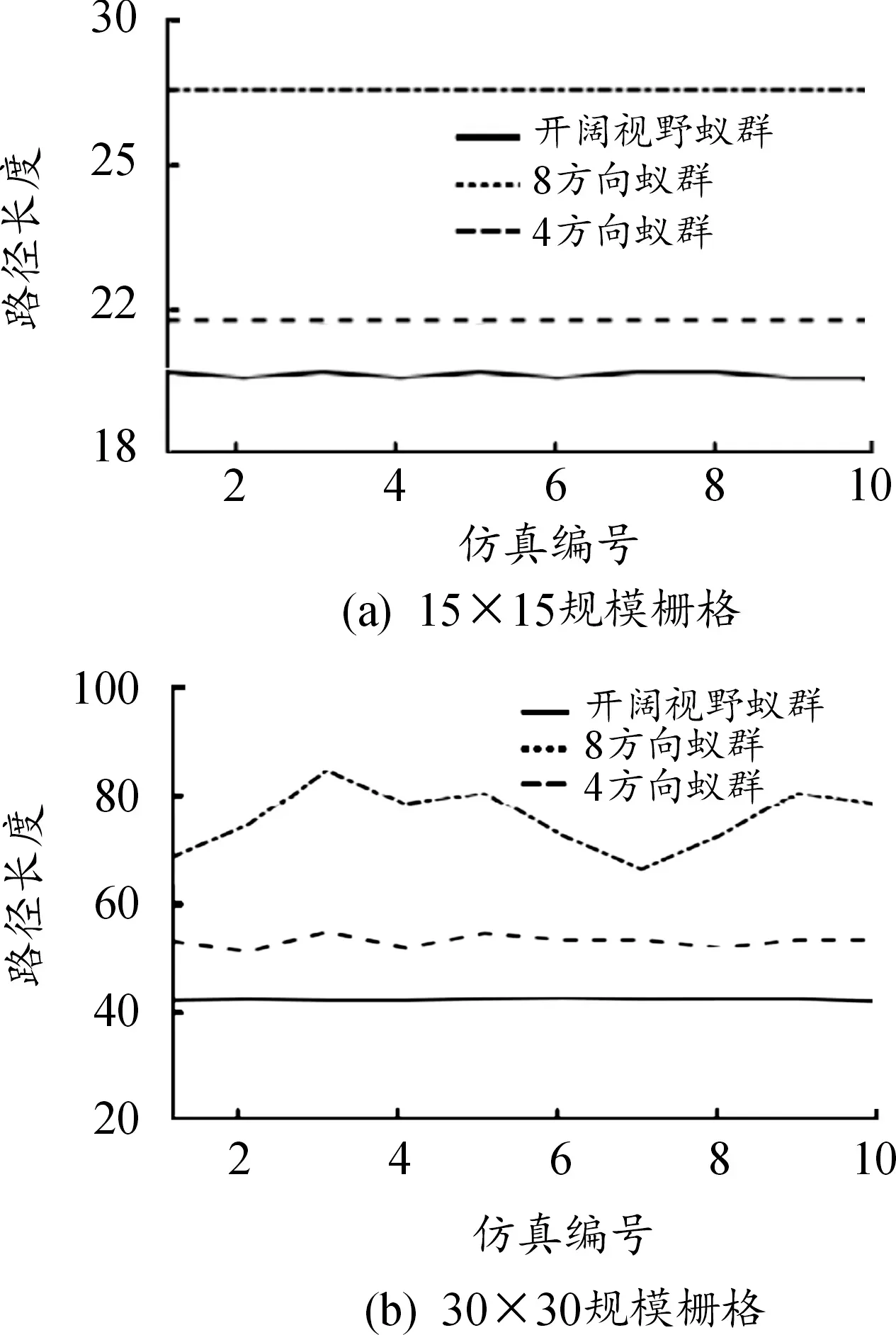
图6 不同算法的10次路径规划结果曲线

由10次规划路径的长度可以看出，4方向蚁群算法的路径长度最大，其次为8方向蚁群算法，开阔视野蚁群算法的路径长度最小，这是因为开阔视野蚁群算法中蚂蚁具有较大视野，蚂蚁运动的机动能力较强，路径转弯的角度最小分辨率仅为22.5°，转角分辨率远远高于4方向蚁群算法和8方向蚁群算法。另外，由于本文蚁群算法具有较大的视野，当蚂蚁选择两步可达栅格时，则算法规划1次相当于另外2种算法规划2次。因此在10次规划结果中，开阔视野蚁群算法规划的路径长度远小于另外2种方法。以30×30规模栅格环境为例，给出3种蚁群算法的最短路径，结果如图7所示。

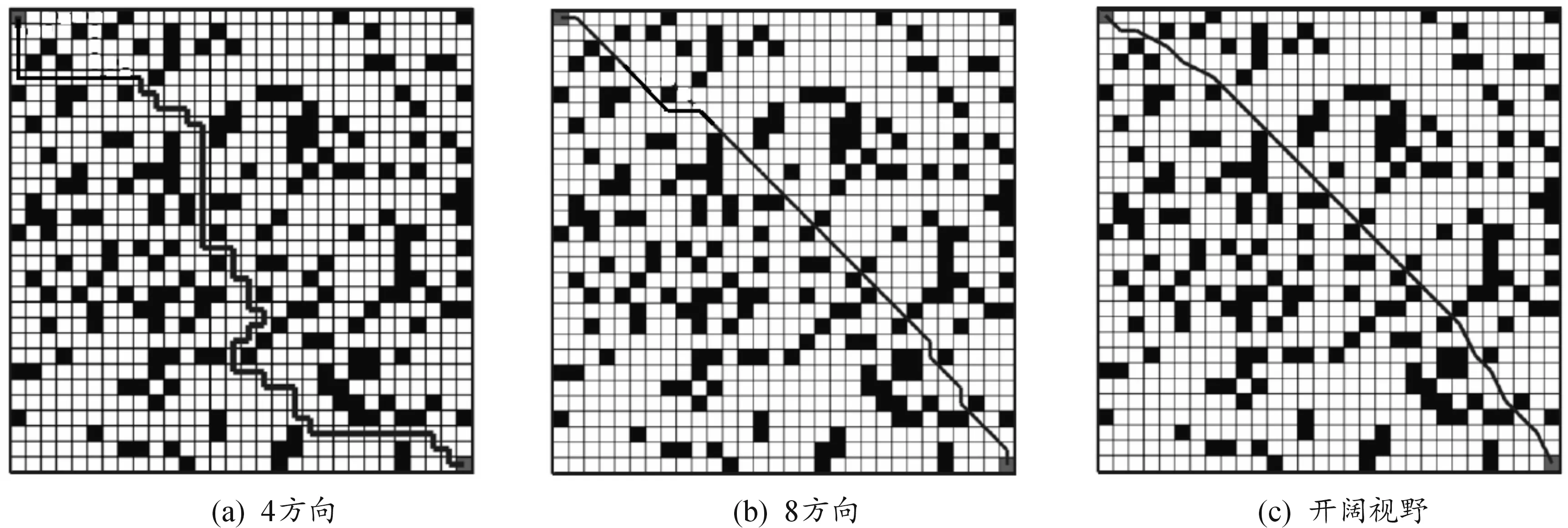
图7 不同算法规划的最短路径

从图7中可以明显看出，开阔视野蚁群算法规划的路径最为光滑，不存在路径折返现象。8方向蚁群算法规划的最短路径光滑性次之，4方向蚁群算法规划的最短路径光滑性最差，且存在一定的折返现象。为了进一步进行比较，统计3种蚁群算法规划路径的长度、迭代次数，结果如表2所示。

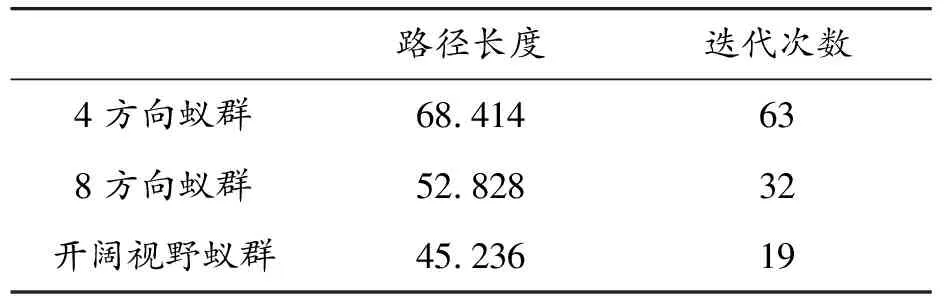
表2 不同算法的规划参数

由表2中数据可知，在30×30规模的栅格环境中，开阔视野蚁群算法规划的最短路径长度为45.236，比8方向蚁群算法减少了14.37%；比4方向蚁群算法减少了33.88%。这是因为开阔视野蚁群算法中蚂蚁活动的机动能力强、路径平滑性好。从迭代次数的角度看，开阔视野蚁群算法迭代19次搜索到最短路径，8方向蚁群算法迭代了32次，4方向蚁群算法迭代了63次，这是因为开阔视野蚁群算法的蚂蚁视野范围广、机动能力强，当蚂蚁选择2步可达栅格时相当于另外2种算法迭代2次，因此开阔视野蚁群算法的迭代次数较少。综合以上分析可知，本文提出的栅格环境下开阔视野蚁群算法的路径规划方法可以有效减少路径长度、提高路径平滑性。

4 结论

1) 开阔视野蚁群算法规划的路径长度小于4方向蚁群算法、8方向蚁群算法；

2) 开阔视野蚁群算法的蚂蚁转角分辨率较高，因此路径平滑性优于另外2种算法；

3) 开阔视野蚁群算法的收敛速度更快，收敛次数少于另外2种算法。