转化思想在小学数学教学中的运用——以“图形与几何”教学为例

林丽琴

（古田县大桥中心小学，福建 古田 352259）

《义务教育数学课程标准（2011年版）》提出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”这一表述强调了数学思想的重要性和重视数学思想的贯彻落实。转化思想是小学数学教材中众多思想方法的基石，是重要且常用的一种方法,例如数形结合体现了数和形互相间的转化，函数思想表明了方程、函数和不等式之间的转化。掌握转化思想不但能提高学生思维品质，而且是解决攻克各种复杂问题的法宝之一。[1]那么如何把转化思想渗透在“图形与几何”的教学中呢？

一、挖掘文本，培养转化意识

教材是知识的载体，蕴含许多解决问题的数学思想方法。但是教材呈现给学生的只是静态的例子，它没有明确地揭示其知识结构中包含的转换思想。因此在教学中，教师要对教材进行深入的分析和研究，不仅要掌握教材的结构和体系的地位和作用，还要把握转化思想的本质，从素材中提炼转化思想，用知识里蕴含的“魂”去培养学生的数学思想，在设计教学方案时要体现数学思想方法的目标。

在小学数学“图形与几何”教学中，转化思想的体现随处可见：把三角形的三个内角转化为平角、三角形与多边形的内角和学习中蕴藏着转换的思想；平面图形面积公式的推导过程用到了转化；立体图形体积之间的互相转化。

就以苏教版五年级上册《平行四边形的面积计算》为例谈谈怎么挖掘教材站在儿童的立场进行教学。在设计教学方案之前，先要考虑学生已有的知识储备：学生已经掌握了长方形和正方形特征以及它们的面积公式，还认识了平行四边形、三角形和梯形的特征；学生已经接触过“转化”思想，但是平面图形的转化还是第一次接触。基于以上的理解和分析，从学生实际出发，笔者进行了如下的教学设计：

先出示两块土地（如图1），

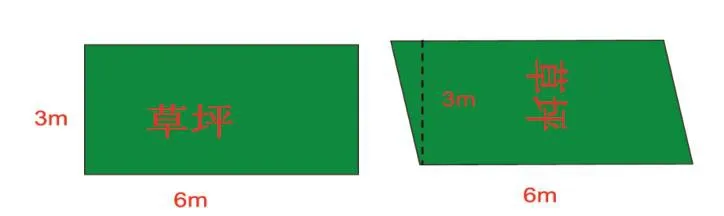
图1

再引导学生比较两块绿地的面积大小，学生利用长方形面积公式算出第一个图形面积，引发了认知冲突。接着让学生通过观察分析，探索交流，在多种观点和方法的不断碰撞中“拨乱反正”，找出正确的推导方法，渗透了图形转化思想。最后回顾反思，拓展延伸时，再一次启发学生利用转化思想去解决新问题，为以后平面图形面积推导埋下了转化思想的“种子”。

数学知识之间的联系非常紧密，环环相扣，而转化思想像一根无形的线将这些知识串联起来。在实际教学中，我们要深入钻研教材，努力挖掘教材中蕴含的转化思想，精心设计教学过程，让这根“无形”的线变得“有形”，从而发展学生空间观念，培养学生转化意识。

二、抓实过程，感悟转化策略

正如苏霍姆林斯基所言：“教师要慷慨地提供事实，而吝啬地给予概括。”的确，在新知识形成发展过程中，教师不仅需要关注学生充分参与研究活动的过程，更要关注学生的思维现状，及时把握运用转化思想的契机，在学生产生内在的迫切需求时，引导学生找到绝佳途径，从而形成正确而深刻的认识和观念，发展转化意识。

比如著名特级教师徐长青执教《多边形内角和》一课时，深入挖掘了教材蕴伏的转化思想，授课时把重点落在如何让学生从浅层的操作活动中去领悟转化思想的巧妙作用，发展转化意识。

徐长青老师先让学生用自己喜欢的方法验证“正方形、长方形、梯形、平行四边形内角和都是360°”这一知识点，学生操作后汇报交流，教师追问：“刚才我们使用了算、量、拼、分四种方法，你最喜欢哪种？为什么？”学生通过比较，得出用“分”的办法误差最少，可以得到最准确的值。

在优化验证方法后进一步引导学生思考：为什么把它分成三角形，而不分成四边形、五边形、六边形呢？在辨析思考中学生形成了“把不熟悉的图形转化成学过的图形”的转化策略。学生有了运用三角形内角和的经验去探索四边形的内角和的策略意识，自然就运用这个方法掌握了求五边形、六边形等多边形内角和的方法。

教学中教师引领学生经历了观察——操作——类比——归纳等一系列活动，帮助学生体验应用“转化”方法解决新问题的过程，这个过程不仅是探索新知的过程，也是一个创新的过程，在这个过程学生学会了把陌生的问题转化为熟悉的问题，体会到转化这个思想方法的妙处，并认识到以前的问题、结果或方法可以随时为我所用去解决新问题，为看问题增添了一个新视角。[2]

三、实践运用，提高转化能力

“纸上得来终觉浅，绝知此事要躬行”，学习能力的形成需要一个过程，知识只有通过不断实践，才能转化成能力。学习了转化策略后，只有通过多次渗透,不断强化，让学生有意识、有目的地运用转化策略解决问题，才能使他们更深刻和形象的掌握转化思想，真正了解转化思想的本质，形成转化能力。

例如在学完苏教版五年级下册《圆的面积》这部分内容之后，以教材内容为依托，结合平面图形的知识笔者让学生完成一道练习题（如图2）：这两个圆半径都是一米，你能求出正方形的面积吗？

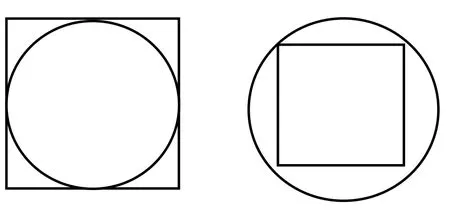
图2

出示题目后先让学生独立思考，一个学生提出来：第一个内圆外方的图形能求得出正方形面积，因为边长等于直径，外圆内方这个图形不知道正方形边长，无法求出面积。

这时教师相机提出了问题，启发学生思考：

题目中只有一个条件，半径一米，这里的半径和直径跟正方形的哪一部分长度是有关联的？那么正方形面积可以转化为什么？想一想，动手画一画。

学生经过观察、操作、讨论交流发现正方形对角线和圆的直径长度相等，这条直径能把正方形分成两个完全一样的等腰直角三角形，半径就是三角形的高，这样就可以把正方形面积转化成两个三角形面积之和了。

这两道题是对比练习，第一小题用常规思路就能解决问题，第二小题则打破了求正方形面积就要知道边长的思维定势，激起学生的探究欲望，学生巧妙运用转化策略求出了正方形的面积，真正地领悟到了转化策略的魅力。

体积计算是小学六年级的重点学习内容，这部分内容让转化思想发挥得淋漓尽致，除了在体积的推导过程中用到转化策略，在很多经典练习题中也有转化的“影子”：比如探索不规则物体体积计算采用的“排水法”，就是把不规则的物体放入装有水的容器中，把“无形的物”转化为有形的“圆柱水”“长方体水”，通过水面上升（或下降）的高度，运用体积公式解决问题。又如图3所示这道题：在一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？

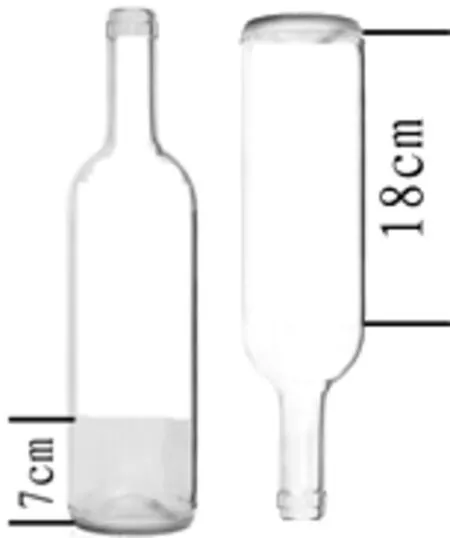
图3

根据题意可知，后面瓶子中的空余部分就是前面瓶子的空余部分，把不规则的瓶子的容积转化为两个圆柱体的容积，根据圆柱的体积=底面积×高，列式解答即可。[3]

只有在应用实践中加强知识的沟通与联系，运用转化策略解决实际问题，转化思想才会随“题”潜入“心”，在不断感悟和反思中深化转化的策略，提高转化的能力，最终达到在数学的世界里举重若轻的境界。

数学思想方法是数学的灵魂，要让学生深入到“转化”这个“思想灵魂”的深处，使转化思想牢牢根植于学生心中，是一个漫长的过程，要把转化思想贯穿于教学的始终，点点滴滴日积月累地不断渗透和训练，让学生养成转化习惯，灵活运用转化方法，才能实现小学数学图形与几何教学的“智慧课堂”。