在推理中积累思考的经验——以《运算律》单元教学为例

陈幼玲

（古田县第二小学，福建 古田 352200）

培养学生的推理能力、帮助学生积累数学活动经验是数学课程标准的要求。数学推理是“人们在数学观念系统作用下，由若干数学条件，结合一定的数学知识、方法，对数学对象形成某种判断的思维操作过程”。[1]小学阶段的数学推理主要包括含有归纳、类比等以经验和直觉为依据的合情推理，以及以确定发展为依据的演绎推理。[2]《义务教育数学课程标准（2011年版）》认为，合情推理就是“从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果”；演绎推理就是“从已有的事实和确定的规则出发，按照逻辑推理的法则证明和计算”。思考的经验是学生“在思维操作中开展活动获得的经验，如归纳的经验、类比的经验、证明的经验。”[3]如果教师在教学过程中引导学生充分经历推理过程，就能有效培养他们的推理能力，帮助他们积累数学思考的经验，教学就会一举多得、事半功倍。现以北师版四年级上册《运算律》单元的教学为例，谈谈如何引导学生在推理过程中积累数学思考的经验。

一、推理中形成思考的经验

数学思考是数学教学的核心。它是学生对数学对象理解和掌握的过程，是学生从数学角度理性思维发现数学现象、用数学知识和方法解决问题的过程。为了帮助学生形成数学思考的经验，教师要引导学生独立、自觉地深入数学学习过程，在具体的教学情境中经历分析、对比、归纳、整理、判断、推理等思维过程，帮助他们在揭示知识本质的过程中逐渐形成数学思考的独特经验。

教学加法交换律时，学生口算4+6和6+4并用4+6=6+4表示后，照样子写出算式2+3=3+2，62+53=53+62，234+567=567+234……学生经过仔细观察，发现交换两个加数的位置，和不变。用生活中的事例解释发现时，有的画图（图1）验证，从电影院到学校的距离和从学校和到电影院的距离一样；有的举例验证：四年级1班有27名男生和24名女生，用27+24或24+27计算，结果都表示全班人数……用a、b表示两个加数时，他们很快用a+b=b+a表示加法交换律。最后，学生用规律解释358+276竖式计算和276+358验算的道理。

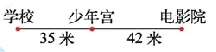
图1

教学乘法交换律时，学生先由3×5=15和5×3=15引出3×5=5×3，接着举出类似例子发现“两个数相乘交换乘数的位置积不变”的规律，然后解释发现，并用含有字母的式子表示规律——a×b=b×a，再用规律解释5×107=535和验算107×5的道理，最后比较两个运算律的异同，理解并掌握规律的内涵。

学生模仿举例中用了类比推理，初步感知交换律；学生发现交换律的过程用了归纳推理，体验了规律抽象概括过程，初步形成归纳的经验——个例猜想不能表示普遍规律，必须通过验证；应用规律解释算理是演绎推理（如大前提是a+b=b+a，小 前 提 是 358+276=634，结 论 是276+358=634）的过程，学生从中初步形成数学思考的经验——简单演绎推理有利于掌握知识本质。探究乘法交换律时，学生刚形成数学思考的经验得到了丰富。

二、推理中丰富思考的经验

数学思考经验是学生直接或间接参与数学思维活动产生形成的。教师要充分引导学生经历数学思考过程，关注学生思考什么，怎么思考，思考结果怎样等。教师要引导学生充分经历观察、操作、实验、猜想、验证、归纳和类比等数学活动，成为他们形成数学思考经验的开发者和促进者，帮助他们在推理过程中形成思考的经验。

教学加法结合律时，教师先引导学生观察（4+8）+ 6 = 4 +（8 + 6）和（19 + 62）+ 38 =19+（62+38）两组等式，再模仿举例。学生经过仔细观察提出猜想——三个数相加，先算前两个数或先算后两个数相加和不变。解释发现时，有的用桃30个梨40个和苹果50个为例说明求总数，可以用（30+40）+50或30+（40+50）表示；有的用一只足球20元、一只游泳圈23元和一只篮球6元为例说明（20+23）+6=20+（23+6）都表示三种体育用品的单价之和……最后，学生用字母a、b、c表示规律——(a+b)+c= a+(b+c)，并用所学知识计算57+288+43，发现应用加法交换律和结合律能使计算简便。

教学乘法结合律时，学生由（2×4）×3=24和2×（4×3）24想到（2×4）×3= 2×（4×3），照样子写出一些例子后发现规律——三个数相乘，先把前2个数相乘或先把后两个数相乘积不变，然后用生活中的事例解释发现：有的用方块拼图解释，有的用买饮料的例子解释……再尝试用含有字母的式子表示规律——（a×b）×c=a×（b×c），最后思考如何计算125×9×8。他们在观察算式中的运算符号和数的特点中加深理解和掌握乘法结合律。

学生探究结合律所经历的归纳推理和演绎推理的过程与交换律的过程相似。他们在类比推理中写出相似算式，在归纳推理中经历规律的抽象概括过程，在应用规律中借助演绎推理掌握运算律。他们从中再次形成数学思考的经验：多写一些类似的例子有助于猜想，但猜想只有经过验证才能成为规律；简单的演绎推理有助于理解并掌握结合律的知识本质。这些经验和前面所形成的经验相似，学生在再次推理中“重复”了数学思考的经验，从而丰富了数学思考的经验。

三、推理中深化思考的经验

思考是学生理解和掌握数学知识本质的关键。学生积累数学思考的经验离不开他们已有经验的迁移，也需要他们在经历一些本质相同、形式不一的数学活动中进行改造和提升，才能使思考经验由低层次不断向高层次发展和提升。教师要充分应用各种教学资源，使学生在丰富多彩的学习素材中实现经验的联结，帮助他们在推理过程中不断形成、发展和提升数学思考经验，从而实现经验的积累。

教学乘法分配律时，学生计算贴瓷砖的块数并说说如何计算：根据瓷砖颜色，有的用3×10+5×10计算，有的则用（3+5）×10计算；根据贴瓷砖位置，则用4×8+6×8计算，有的则用（4+6）×8计算，结果都是80块。观察两组算式时，他们根据瓷砖颜色和位置分别写出算式3×10+5×10=（ 3+5）×10和 4×8+6×8=（4+6）×8，并类比写出更多相似例子，尝试描述乘法分配律：一个数乘两个数的和等于这个数分别乘这两个数所得积的和，并用a、b、c表示规律（a+b）×c=a×c+b×c。结合算式4×9+6×9说明乘法分配律时，有的学生画点子图（图2）说明，有的学生直接用4个9加上6个9，一共10个9，就是（4+6）×9进行说明。最后，学生分别观察（80+4）×24和34×72+34×28的特点，在应用中理解并掌握乘法分配律。

图2

用字母表示乘法分配律是由特例的共性特点归纳概括出一般性结论的过程，从抽象竖式回归现实，借助图形直观解释发现，进一步认识乘法分配律。在探索运算律的过程中，学生又经历了一次推理过程，并形成新的思考经验：类比和归纳在探究规律中必不可少；解释说明规律可以画图，也可以直接表达；应用规律简便计算需要会讲道理。学生数学思考的经验不是简单重复，而是螺旋上升，不断深化和提升。

总之，学生在究性学习，很好地经历了推理过程。学生通过观察、仿写、解释和表达活动，自主发现问题、提出问题、归纳和总结规律，不但提升了数学思维能力，而且感悟了推理思想，还积累了数学思考的经验。当然，他们积累数学思考的经验是一个循序渐进的过程。教师要引导学生一方面在推理中获得经验，另一方面要在推理中丰富和深化思考经验，使学生在循序渐进中不断提升活动经验。