高考题怎么改编（二）——函数与性质篇

苏 玖

真题展示

问题1（2018年全国Ⅱ卷第11题）已知f（x）是定义域为（－∞，＋∞）的奇函数，满足f（1－x）＝f（1＋x）．若f（1）＝2，则f（1）＋f（2）＋…＋f（50）＝（ ）

A．－50 B．0 C．2 D．50

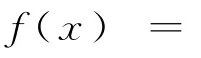
思维延伸

问题1思维延伸如果已知和式的值求自变量的值，也就是多少个连续的函数值等于已知数，就有：

（改编1-1）已知f（x）是定义域为（－∞，＋∞）的奇函数，满足f（1－x）＝f（1＋x），f（1）＝2，Sn＝f（1）＋f（2）＋…＋f（n），若Sn＝0，则n的取值集合为________．

如果将“奇函数”改为“偶函数”，再改变相关条件，于是就有：

（改编1-2）已知f（x）是定义域为（－∞，＋∞）的偶函数，满足f（x－1）＝f（1＋x），在［0，1］上f（x）＝2x2－1，若则a的所有值构成的集合为________．

（改编1-3）已知f（x）是定义域为（－∞，＋∞）的奇函数，满足f（1－x）＝f（1＋x），f（x）在［0，1］上单调递增，且f（x）在 ［0，2）上有唯一零点．若函数在区间［0，n］上有100个零点，求最小正整数n的值．

问题2思维延伸本题就是周期函数、分段函数与函数迭代的综合应用，周期函数与分段函数是必考的知识点，画图可以看出，一个周期内f（x）有两个零点和1，于是从图象角度可以改编为：

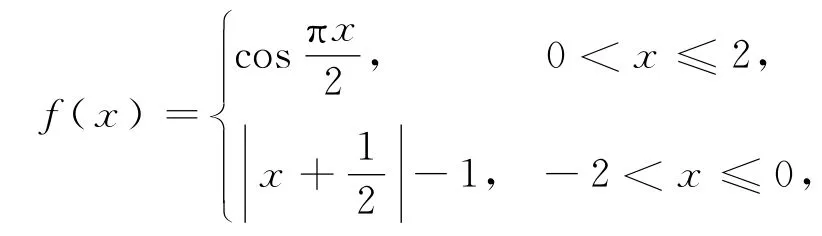
从函数迭代角度出发，条件不变，待求改变，于是又可以改编为：

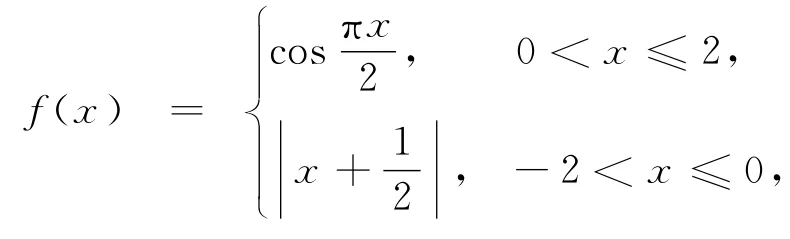
如果将分段函数改编为待定函数，可以改编为：

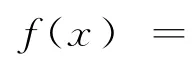
点拨解析

问题1的解析：f（x）是奇函数，因此f（0）＝0．又因为f（1－x）＝f（1＋x），因此f（x）的图象关于直线x＝1对称．又有f（－x）＝f（2＋x），即f（2＋x）＝－f（x），所以f（2）＝0，f（x＋4）＝f（x），故函数f（x）是周期函数，周期为4．因为f（1）＝2，f（3）＝f（－1）＝－2，f（4）＝0．因此一个周期内的和为0，所以f（1）＋f（2）＋ … ＋f（50）＝f（1）＋f（2）＝2，故选C．

改编1-1解析：分类讨论，因为一个周期内的函数值之和为0，因此当n＝4k，k∈N*时，Sn＝0；当n＝4k－1，k∈N*时，Sn＝f（1）＋f（2）＋f（3）＝0；当n＝4k－3，k∈N*时，Sn＝f（1）＝2；当n＝4k－2，k∈N*时，Sn＝f（1）＋f（2）＝2．所以n的取值集合为｛n|n＝4k－1或n＝4k，k∈N*｝．

推广：已知f（x）是定义域为（－∞，＋∞）的奇函数，满足f（1－x）＝f（1＋x）．若f（1）＝a，求：（1）Sn＝f（1）＋f（2）＋…＋f（n）；（2）

提示：分类讨论得：

改编1-2解析：由f（x－1）＝f（1＋x）知，f（x）是周期为2的周期函数，当x∈［－1，1］时，f（x）＝2x2－1，同时图象关于直线x＝1对称，因此对称轴是x＝k（k为整数），当a∈［－1，1］时即．由周期性，所有的a的值为所以a的取值集合为

改编1-3解析：由题意得，函数f（x）的周期为4，图象关于直线x＝k（k∈Z）对称．因为f（x）在［0，1］上单调递增，因此f（x）在［－1，1］上单调递增，且f（x）在［－1，1］上有唯一零点0．由于f（0）＝0，因此f（2）＝0，所以f（x）在一个周期内［0，4）上有零点0和2．又因为函数是f（x）图象向右平移个单位长度得到的，于是g（x）在一个周期内［0，4）上有零点和．要使g（x）在［0，n］内有100个零点，因此区间［0，n］内必有50个周期，而这些零点分别为…，构成等差数列，公差为2，第100个零点为，所以故最小正整数n为199．

问题2的解析：由题意知，f（x）是周期为4的函数，，因此所以填

改编2-1解析：画图分析，区间［－4，10］内有三个半周期，要使得有10个零点，一个周期内至少要有三个零点，于是

若本题改为g（x）在区间［－4，10］内有11个不同的零点，则实数a取值范围为_________．在x＝－4时，图象为一个点答案为

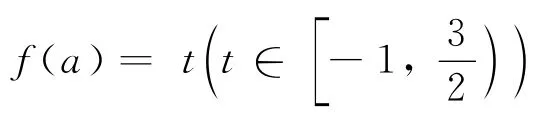
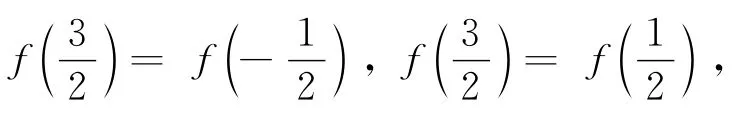
回顾悟道

通过对两道高考题的分析和改编，可以看出，求解函数与性质问题时，一要会很快理解题目所给的各类信息；二要学会综合分析信息之间的关系，进行信息加工；三是对某一个信息进行改编，就可以得到不同的题目，通常是“常量”变“参数”，“静态”变“动态”，“结论”变“条件”，“单参数”变“双参数”等等．

小试牛刀

A．［－1，0） B．［0，＋∞）

C．［－1，＋∞） D．［1，＋∞）

若改变函数f（x）中某一段解析式（平移或伸缩），而g（x）中的a为具体数，试试看．

改编1：______________________________．

原题中的问题是f（x）图象与斜率为定值的一次函数交点问题，如果改为研究过定点的一次函数与f（x）图象交点问题．

改编2：______________________________．

提示与解析：

原题解析：问题等价转化为y＝f（x）与y＝－x－a的图象有两个交点，结合函数图象得，－a≤1，即a≥－1，故选C．

答案：a≥1．

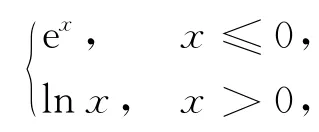
答案：－1≤a＜0或0＜a＜1或a＞1．