由一道函数题的错解引发的探索和思考

毛雨萱

一、问题与背景

在复习导数在函数与方程中的应用时，老师给我们布置了这样一道习题：

已知函数f（x）＝kx，，求方程f（x）＝g（x）在区间内解的个数．

这道题求解的方法我们都很明确：利用导数工具画出函数的图象，利用图象数形结合求解．但是，在具体操作时，不同的处理方法，得出了大相径庭的结果，一时间我们都感到有点奇怪和不解．

二、思路与解法

我的解题思路是参变分离：

由 方程f（x）＝g（x），得

于是，h（x）在上单调递增，在上单调递减，且于是由图1得：

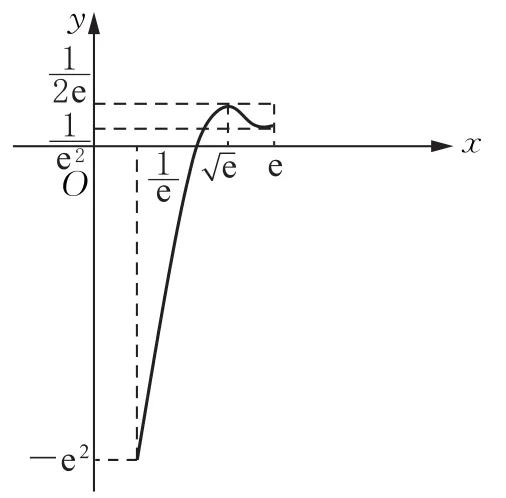
图1

同学的思路也是参变分离：

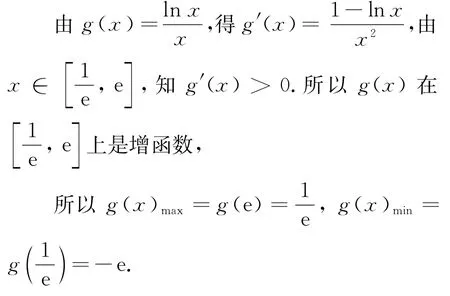
函数g（x）在上的近似图象如图2所示，

于是直线OA斜率直线OB斜率kOB＝－e2，

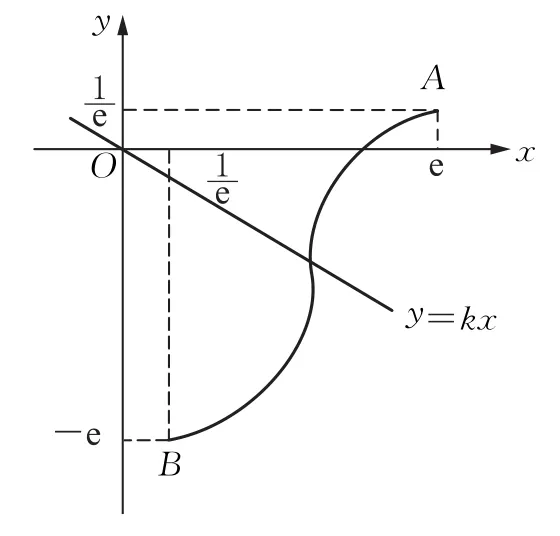
图2

三、质疑与探索

我和同学的解法都是将方程的根转化为两个函数的图象的交点来判断，这是求解有关函数零点个数（方程解的个数）问题的通法，看起来都有理有据，但结果却迥然不同，孰对孰错？错在哪里呢？

我和同学们展开探究和讨论．我的解法是将问题转化为函数y＝k与的图象的交点个数来判断．水平直线y＝k与的图象的交点，根据的单调性，容易结合图象作出判断，我的解法应该是正确的．而同学的解法是斜线f（x）＝kx与的图象的交点仅根据的单调性是不够的，必须更精确地画图以表现出此函数的基本性态，我怀疑他的图象不准确，故而借助MathPac软件模拟了图象，如图3．

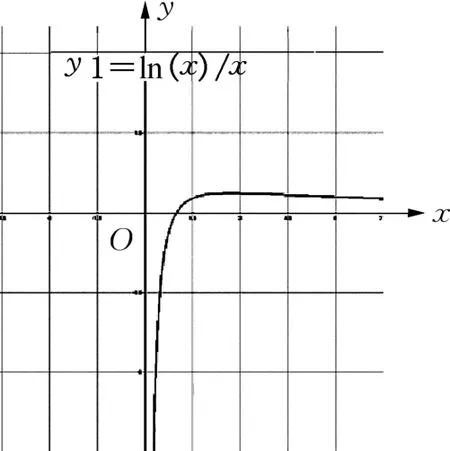
图3

果然是由于g（x）的图象不准确，解题时误以为是k的最大值，忽视了在A点左侧会因曲线向上弯曲（上凸），且曲率较大时，直线y＝kx过A点时会和曲线g（x）有另一个交点（在A点左侧），此时k的最大值应在与曲线相切时取得．

经过查阅资料和对问题的探究找到问题的根源，由同学的解法知在上是增函数，又，当时在上是上凸函数，于是我们可以作出g（x）的更精确的图象如图4，函数f（x）＝kx与的图象在在内有相切的情况．

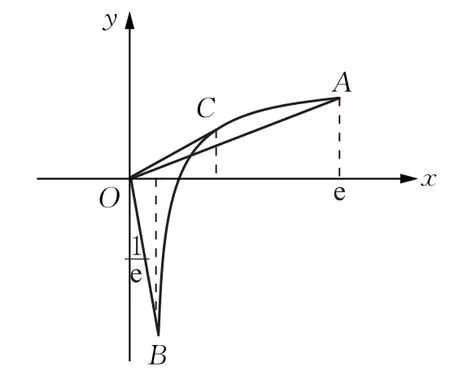
图4

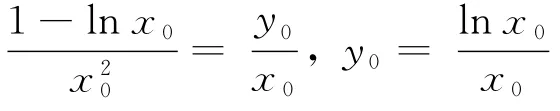
通过分析，除了我和同学的解法之外，还获得了一种得到全班都认可的解法，同时也解释了上述剖析的正确性和上述错解的根源．

令f（x）＝g（x），即即kx2＝lnx，在同一个坐标系中画出函数y＝kx2和函数的图象，如图5．函数y＝kx2随着k增大，图象从开口方向向下，逐渐变化为一条直线（k＝0），再变化为开口向上，在开口向上时开口逐渐减小．因此，图象在从开口向下逐渐变化的过程中，首先经过点此时k＝－e2，然后变化为一条直线y＝0，此时k＝0，当k＞0时函数y＝kx2的图象逐渐变化到经过点（e，1），此时与函数的图象有两个交点，然后变化到与函数y＝lnx的图象只有一个交点（相切），此时，求解过程如下：

图5

当k＜－e2时方程无解，当－e2≤k＜时方程有一解，当时方程有两解，当时方程有一解，当时方程无解．

四、思考和感悟

从三种解法的探究和分析来看，尽管处理的方法类似，由于方法一转化成的两个函数中有一个是平行于x轴的直线，所以更容易操作，后两种方法对图形的要求则更高；同学解法的错误原因在于“图形”的不准确，因为作图太随意，没有把握住图形的基本特征和关键点，所以作出的图象不能准确地反映出函数的基本形态，再加上简单处理，想当然地得出答案，这样错误的发生就不足为奇了；“数缺形时少直观，形缺数时难入微．”我们在利用数形结合思想解题时要先从数的角度研究出函数的各项性质，再画出函数准确的图象，这样才能真正将数与形完美结合起来为我们所用．